ICS CMS | R. Sauser (EPFL)

7.5 Tableau de Butcher

Dans le cas d'une partition régulière de pas \(h\), une méthode de Runge-Kutta (à un pas, explicite ou implicite) correspond à un schéma général de la forme :

\[ u_{n+1} = u_n + h\sum_{i=1}^{s}{b_iK_i}\,, \]

où

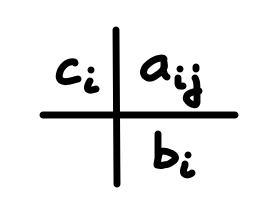
\(s\) est le nombre d'étapes de la méthode,
les \(s\) ''pentes'' \(K_i\), \(i=1,2,\dots s\), sont données par \[ K_i = f(t_n+c_i h, u_n+h\sum_{j=1}^{s}{a_{ij}K_j})\,. \]

Les coefficients \(b_i\), \(a_{ij}\) et \(c_i\) sont souvent donnés dans un tableau de Butcher de la forme :

Ainsi, ce tableau s'écrit pour le schéma RK4 :

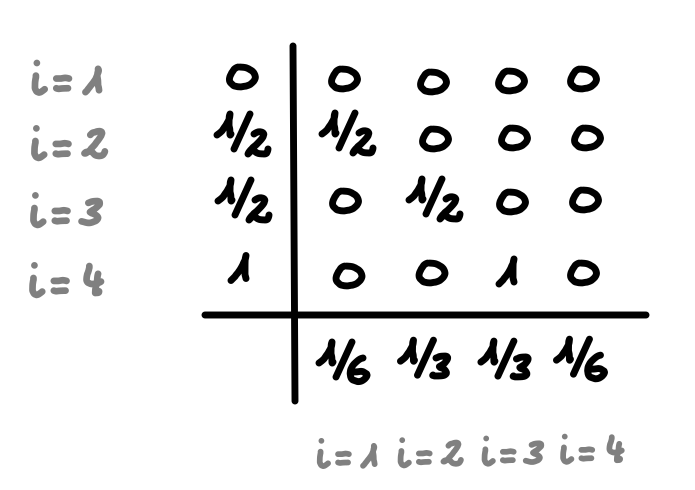
Pour rappel, dans le schéma RK4, les quatre pentes suivantes interviennent :

\[\begin{aligned} K_1 &=f(t_n,u_n) \,\,\leftarrow\text{ (point de gauche)}\\ K_2 &=f(t_{n}+\frac{h}{2},u_n+\frac{h}{2}K_1) \,\,\leftarrow\text{ (prédiction à l'aide d'Euler progressive)}\\ K_3 &=f(t_{n}+\frac{h}{2},u_n+\frac{h}{2}K_2) \,\,\leftarrow\text{ (prédiction à l'aide de } K_2)\\ K_4 &=f(t_{n+1},u_n+hK_3) \,\,\leftarrow\text{ (prédiction à l'aide de } K_3) \end{aligned}\]

et la résolution numérique fait intervenir

\[ \left\{\begin{array}{rcl} u_{n+1} &=& u_n + \dfrac{h}{6}(K_1+2K_2+2K_3+K_4)\,,\\ u_0&=&y_0\,.\end{array}\right. \]