ICS CMS | R. Sauser (EPFL)

5.4 Représentation d'une courbe paramétrée

Représentation en 2D

En deux dimensions, une courbe paramétrée par le paramètre \(t\) est donnée par \(\vec r\,(t) = x(t)\vec e_x + y(t)\vec e_y\), où les vecteurs \(\vec e_x\) et \(\vec e_y\) sont des vecteurs unitaires dans les directions \(x\) et \(y\), respectivement.

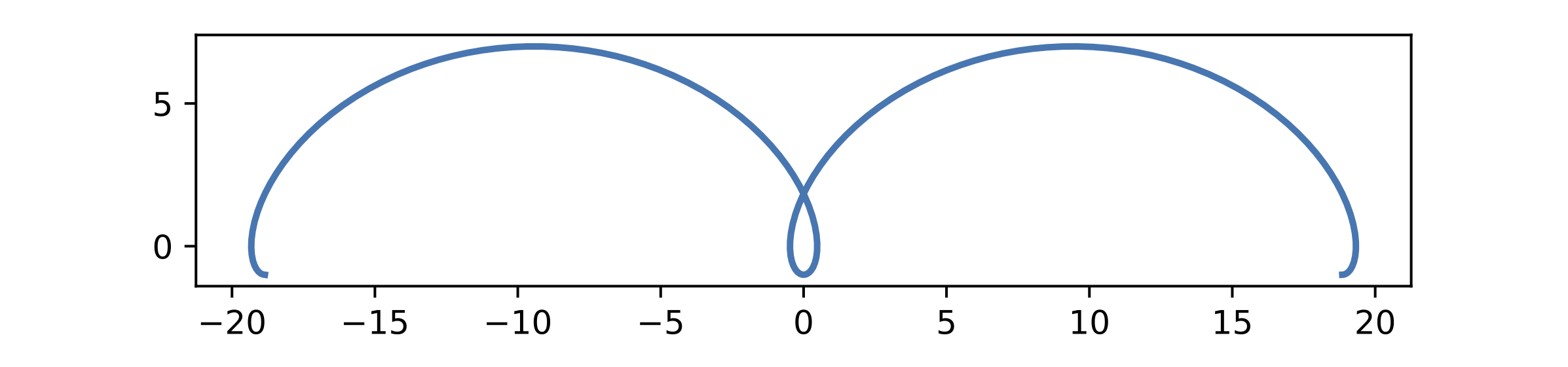
En guise d'exemple, nous allons considérer une courbe appelée trochoïde définie par :

\[ \left\{\begin{array}{rcl} x(t) &=& R\,t-d\sin{t}\,,\\ y(t)&=& R-d\cos{t}\,.\end{array}\right. \]

Remarque: La cycloïde est un cas particulier de cette courbe que l'on obtient en posant \(d=R\). Si vous vous intéressez aux courbes mathématiques en deux et trois dimensions, ne manquez pas de visiter le site suivant : https://mathcurve.com/.

Les coordonnées du vecteur position \(\vec r\,(t)\) peuvent être définies de la manière suivante :


import numpy as np
import matplotlib.pyplot as plt
R = 3
d = 4
t = np.linspace(-2*np.pi,2*np.pi,1000)
courbe_x = R*t - d*np.sin(t)
courbe_y = R - d*np.cos(t)

Après avoir créé les axes, on peut afficher la courbe :


fig = plt.figure(1) 
ax = fig.gca()
ax.plot(courbe_x, courbe_y, linewidth=2)
plt.axis('scaled')
plt.show()

Remarque: On pourrait ici également simplement utiliser le code suivant : plt.plot(courbe_x, courbe_y, linewidth=2) plt.axis('scaled') plt.show()

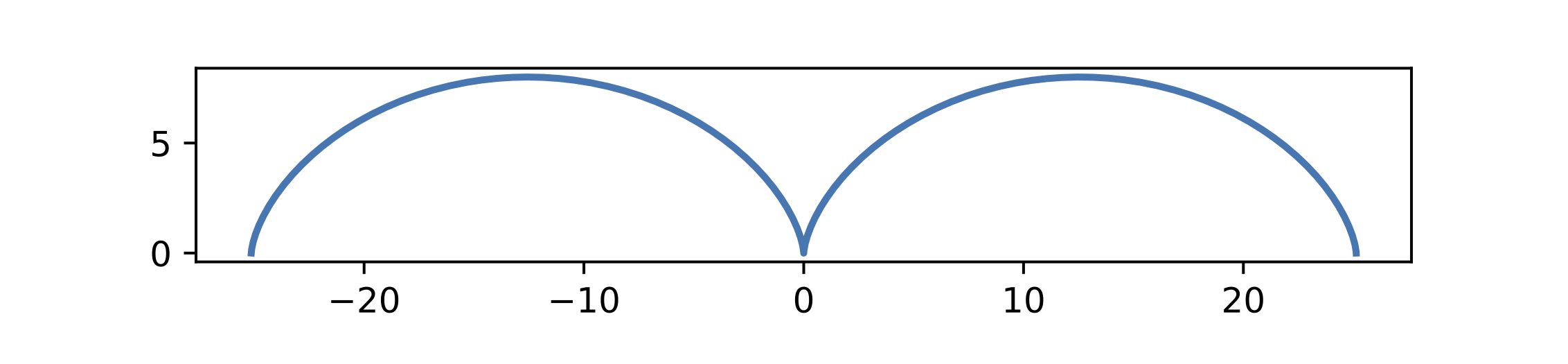
Cas particulier de la cycloïde :

Représentation en 3D

En trois dimensions, une courbe paramétrée par le paramètre \(t\) est donnée par :

\[ \vec r\,(t) = x(t)\vec e_x + y(t)\vec e_y + z(t)\vec e_z\,, \]

où les vecteurs \(\vec e_x\), \(\vec e_y\) et \(\vec e_z\) dénotent les vecteurs unitaires dans les directions \(x\), \(y\), et \(z\), respectivement.

Après le préambule habituel,


import numpy as np
import matplotlib.pyplot as plt

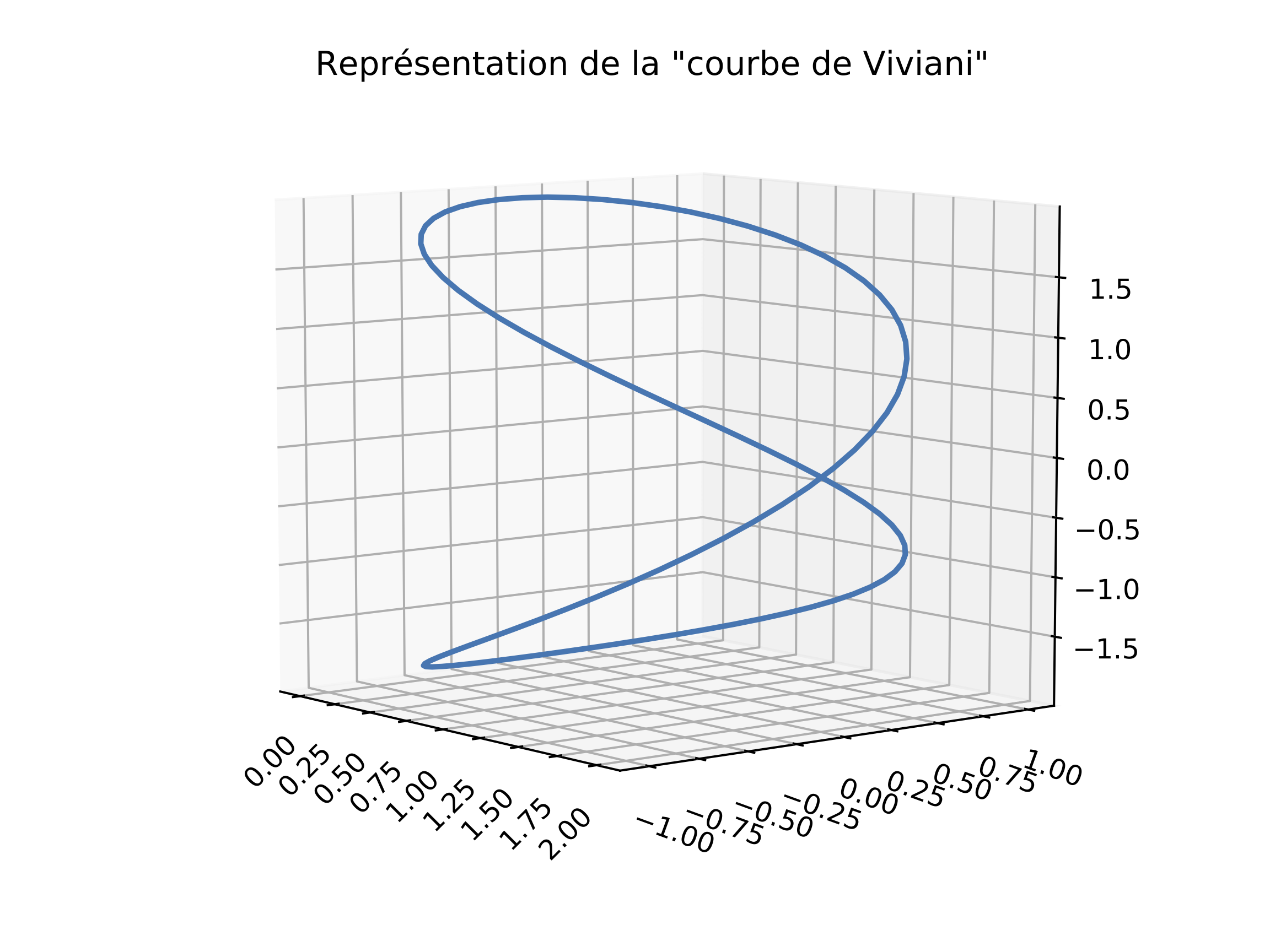
les coordonnées du vecteur position \(\vec r\,(t)\) peuvent être définies de la manière suivante (cas d'une courbe appelée ''courbe de Viviani'') :


a = 1
t = np.linspace(-2*np.pi,2*np.pi,100)
courbe_x = a + a*np.cos(t) 
courbe_y = a*np.sin(t)
courbe_z = 2*a*np.sin(t/2)

Il est alors possible d'afficher la courbe en prenant soin de faire tourner quelque peu les graduations des axes \(x\) et \(y\) pour améliorer la lisibilité de la figure :


fig = plt.figure(1) 
ax = plt.axes(projection='3d')
#ax = fig.add_subplot(projection='3d') # Variante
plt.setp(ax.get_xticklabels(), rotation=45)
plt.setp(ax.get_yticklabels(), rotation=-20)
ax.plot(courbe_x, courbe_y, courbe_z, linewidth=2)
ax.set_title('Représentation de la "courbe de Viviani"')
plt.show()

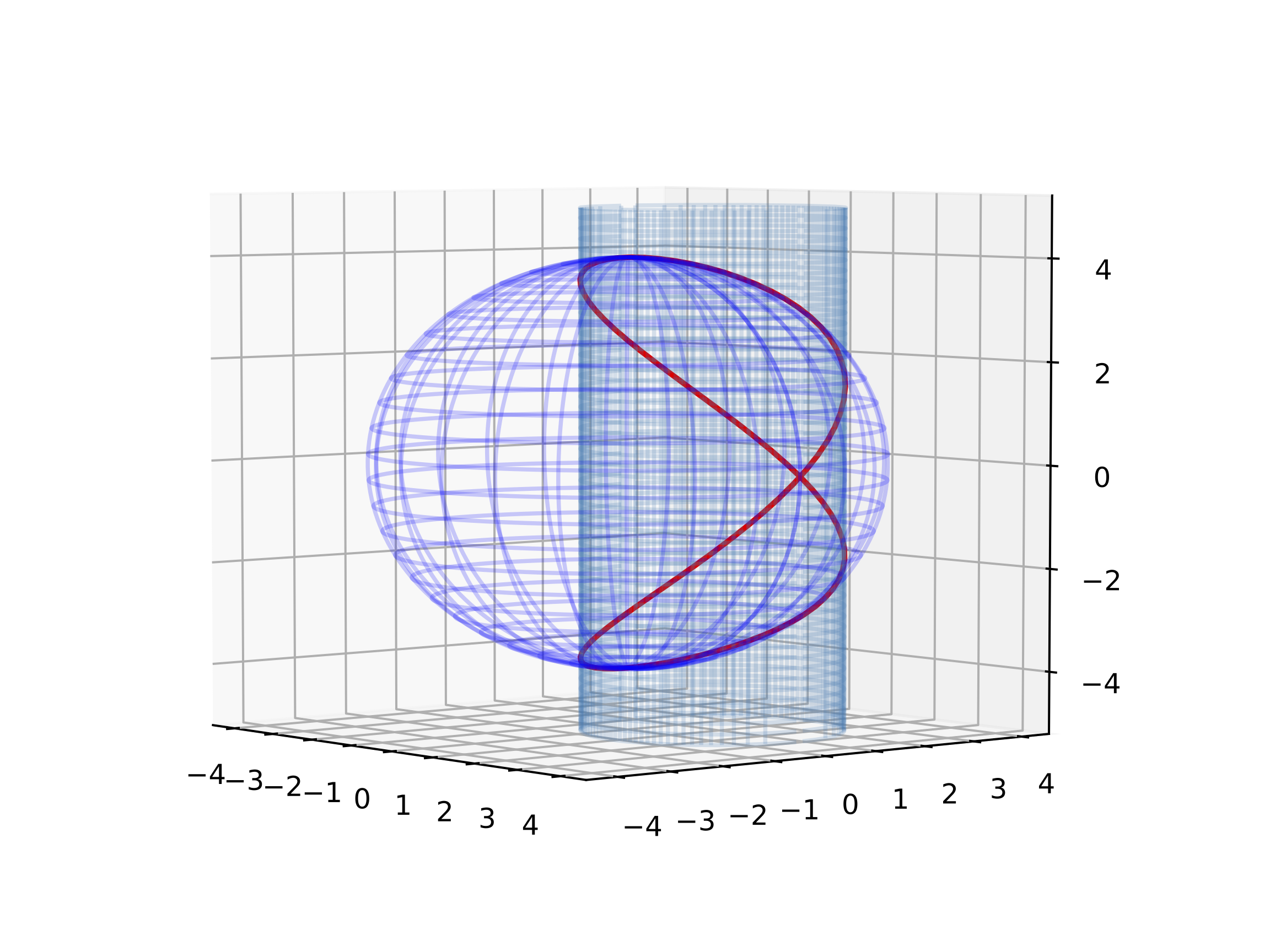
Remarque: La courbe de Viviani (appelée aussi ''fenêtre de Viviani'') est définie comme l'intersection d'une sphère et d'un cylindre qui est tangent à la sphère et passe par le centre de cette dernière :