En physique, certaines grandeurs sont décrites par des champs vectoriels. Ainsi, le champ électrique \(\vec E\) est une grandeur vectorielle dont les composantes varient selon le point de l'espace considéré :
\[ \vec E = \begin{pmatrix} E_x(x,y,z) \cr E_y(x,y,z) \cr E_z(x,y,z) \cr \end{pmatrix}\,. \]De plus, certains de ces champs vectoriels ''dérivent d'un potentiel'', c'est-à-dire d'un champ scalaire. Dans le cas de \(\vec E\), ce champ scalaire est le potentiel électrique \(\phi = f(x,y,z)\). Plus précisément,
\[ \vec E = -\vec{\nabla}\phi = -\begin{pmatrix} \partial\phi/\partial x\\ \partial\phi/\partial y\\ \partial\phi/\partial z\\ \end{pmatrix}\,, \]où \(\vec\nabla\phi\) est appelé le gradient de \(\phi\) et où \(\partial/\partial x\), \(\partial/\partial y\) et \(\partial/\partial z\) sont des dérivées partielles.
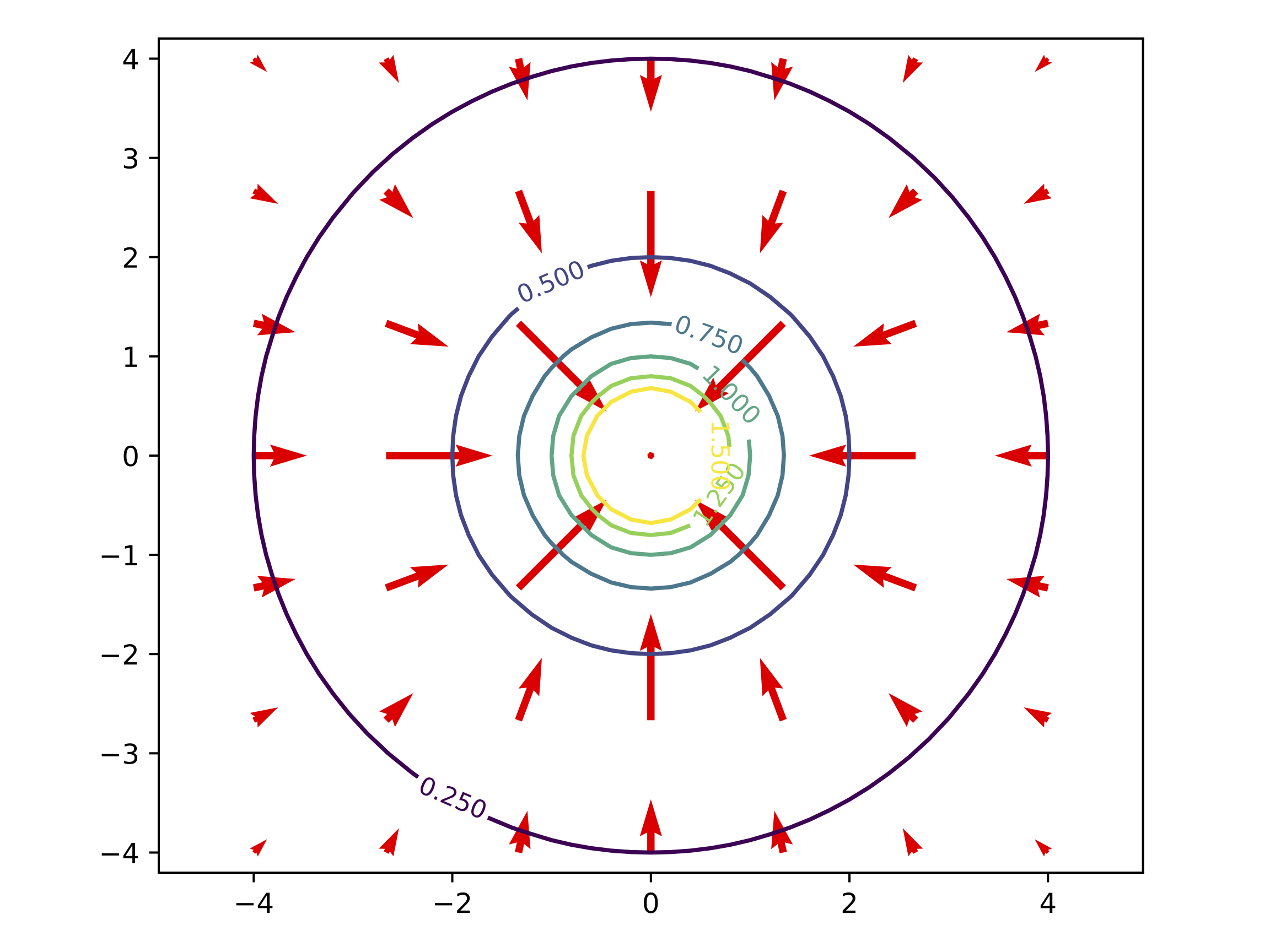
quiverLe gradient d'un champ scalaire en un point est un vecteur pointant dans la direction où le champ augmente le plus (direction de ''plus grande pente''). Il est donc perpendiculaire à la courbe de niveau qui passe par ce point. Ainsi, le champ électrique est toujours orthogonal aux courbes sur lesquels le potentiel est le même (équipotentielles). Nous allons l'illustrer en deux dimensions à l'aide de la fonction scalaire :
\[ \Psi(x,y) = \frac{1}{\sqrt{x^2 + y^2}} \]
dont nous allons représenter des courbes de niveaux accompagnées
de vecteurs gradients. Pour ce faire, nous utilisons la
fonction np.gradient qui retourne le gradient d'un champ
donné comme un tableau
à \(N\) dimensions, ainsi que la fonction ax.quiver qui
permet de représenter un champ bidimensionnel de flèches.
import numpy as np
x = y = np.linspace(-4.,4.,41)
xv, yv = np.meshgrid(x,y,indexing='ij')
Psiv = 1/(np.sqrt(xv**2 + yv**2))
#
x2 = np.linspace(-4.,4.,7)
y2 = np.linspace(-4.,4.,7)
x2v, y2v = np.meshgrid(x2,y2,indexing='ij')
Psi2v = 1/(np.sqrt(x2v**2 + y2v**2))
dPsidx, dPsidy = np.gradient(Psi2v)
#
import matplotlib.pyplot as plt
fig = plt.figure(1)
ax = fig.gca()
niveaux = [0.25, 0.5, 0.75, 1.0, 1.25, 1.5]
cs = ax.contour(xv,yv,Psiv,levels=niveaux)
plt.clabel(cs, inline=True, fontsize=9)
ax.quiver(x2v,y2v,dPsidx,dPsidy, color='r')
plt.axis('equal')
plt.show()
Représentation de quelques courbes \(\Psi=\Psi_0=\text{constante}\) (cercles de rayon \(r=\sqrt{x^2+y^2}\) centrés à l'origine) et de quelques vecteurs gradient \(\vec\nabla\Psi\) :
streamplotMatplotlib permet également de représenter un champ vectoriel sous la forme de lignes de champ. Ces lignes sont tangentes, en tout point, à la direction des vecteurs et permettent d'aisément visualiser l'allure du champ. En revanche, elles ne fournissent pas d'information sur l'intensité du champ, sauf si leurs couleurs, leurs épaisseurs ou leur densité sont significatives.
La fonction streamplot demande :
x et y);
Le paramètre density contrôle l'espacement des lignes du
champ.
La couleur des lignes (gérée par le paramètre color
qui doit alors être un tableau)
permet quant à elle de visualiser la longueur (norme) des vecteurs du champ.
import numpy as np
x = np.linspace(-4.,4.,101)
y = np.linspace(-4.,4.,101)
xv, yv = np.meshgrid(x,y,indexing='ij')
Psiv = 1/(np.sqrt(xv**2 + yv**2))
dPsidx, dPsidy = np.gradient(Psiv)
import matplotlib.pyplot as plt
fig = plt.figure(1)
ax = fig.gca()
t_couleurs = 36*np.log(dPsidx**2+dPsidy**2) # tableau des couleurs
ax.streamplot(x, y, dPsidy, dPsidx, color = t_couleurs,linewidth=1,cmap = plt.cm.plasma, density = 2,arrowstyle = '->', arrowsize = 1.5)
ax.set_title("Lignes de champ du gradient de $\Psi$")
plt.axis('scaled')
plt.show()
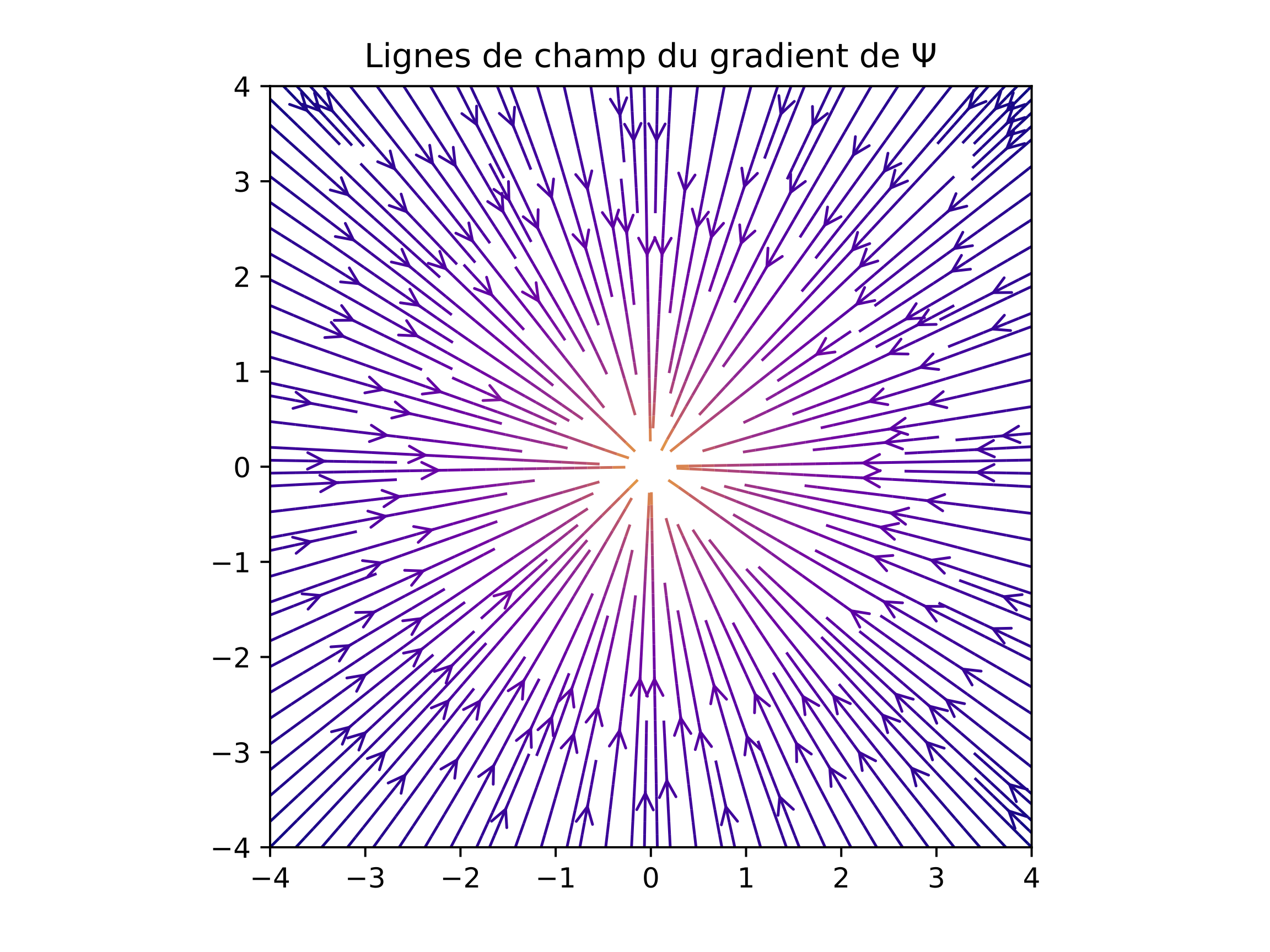
Remarque: les lignes de champ ne se croisent jamais.
Dernière compilation: 2025-05-28 (06:27:05)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
