La température est un exemple de champ scalaire : il s'agit d'une grandeur scalaire dont la valeur (un nombre) varie selon le point de l'espace considéré : \(T=f(x,y,z)\).
Une fonction scalaire de deux variables \(f(x,y)\), par exemple la température sur une plaque (surface), peut être visualisée :
Nous allons représenter le champ scalaire bidimensionnel suivant :
\[ f(x,y) = \frac{10x}{1 + x^2 + y^2}\,. \]np.meshgrid)Avant de pouvoir représenter la fonction \(f(x,y)\), il est nécessaire de créer une grille rectangulaire de points dans le plan \(xy\) :
import numpy as np
x = y = np.linspace(-4.,4.,41)
xv, yv = np.meshgrid(x,y,indexing='ij')
A partir de coordonnées x et y également
espacées, la fonction np.meshgrid produit les coordonnées
''vectorisées'' xv et yv
(xv et yv sont des tableaux \(41\times 41\) de dimension \(2\)).
On calcule alors la valeur de \(f\) aux \(41\times 41\) points de la grille :
fv = 10*xv/(1 + xv**2 + yv**2)
Le résultat retourné, fv, est une matrice \(41\times 41\)
(c'est-à-dire un tableau de dimension \(2\)).
Pour représenter le champ scalaire en deux dimensions, il est nécessaire d'importer Matplotlib, avant de créer une figure et un système d'axes :
import matplotlib.pyplot as plt
fig = plt.figure(1) # pour créer la figure
ax = fig.gca() # pour créer les axes ("get the current axes")
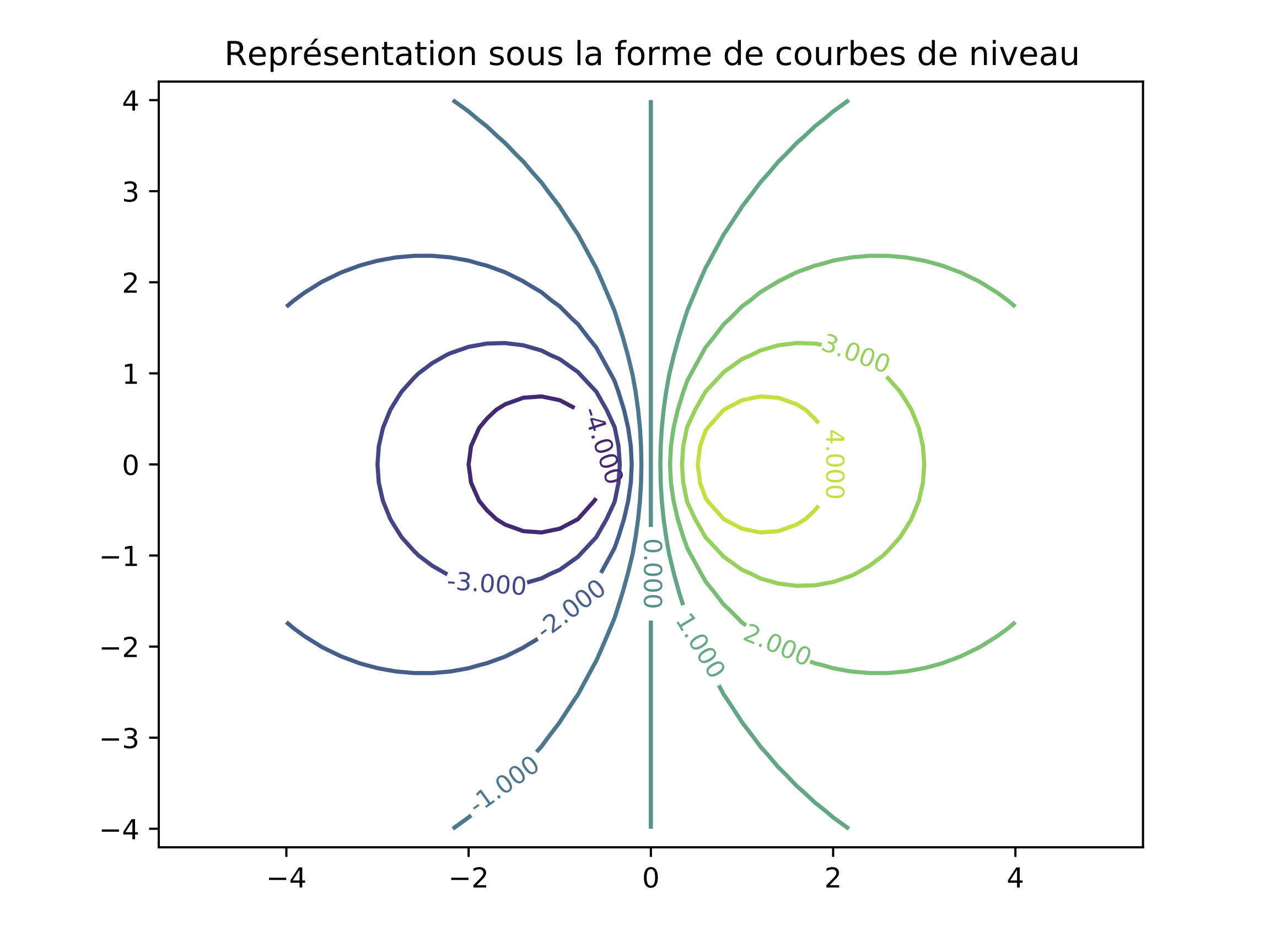
En appelant la fonction contour, on obtient alors,
par exemple, \(9\) courbes de niveau dont les valeurs sont
précisées sur le dessin :
plt.title("Représentation sous la forme de courbes de niveau")
cs = ax.contour(xv,yv,fv,9) # "contour set"
plt.clabel(cs, inline=True, fontsize=9)
plt.axis('equal')
plt.show()
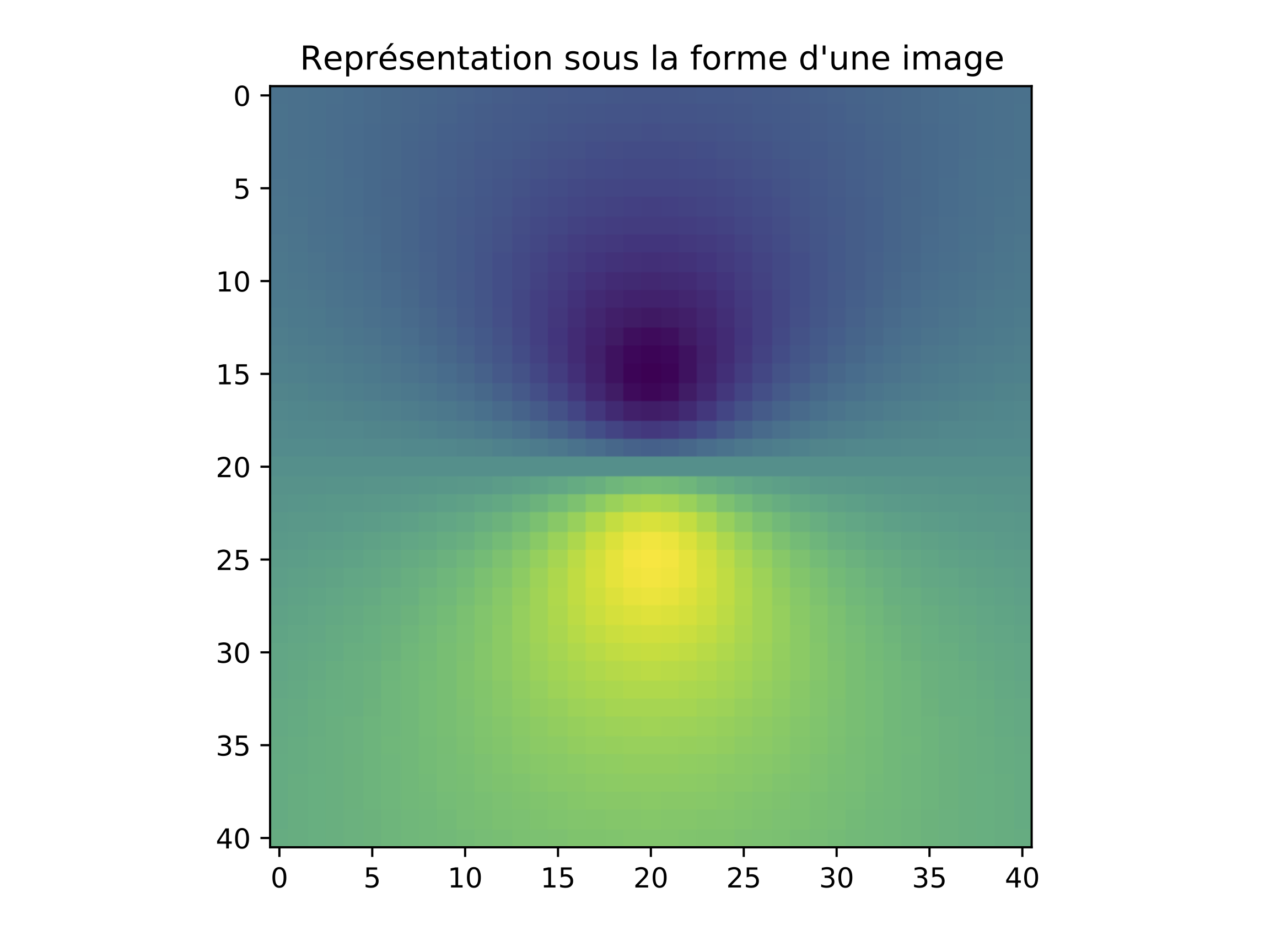
On peut également afficher la fonction \(f(x,y)\) comme une image dont les couleurs reflètent les valeurs que prend la fonction :
import numpy as np
x = y = np.linspace(-4.,4.,41)
xv, yv = np.meshgrid(x,y,indexing='ij')
#
fv = 10*xv/(1 + xv**2 + yv**2)
#
import matplotlib.pyplot as plt
fig = plt.figure(1) # pour creer la figure
ax = fig.gca() # pour creer les axes ("get the current axes")
#
plt.title("Représentation sous la forme d'une image")
ax.imshow(fv)
plt.show()
Types de représentations bidimensionnelles envisageables pour un champ scalaire :
Remarque : la fonction plt.axis('equal') permet de
faire en sorte que l'échelle soit identique sur les deux axes. En remplaçant
'equal' par 'scaled', on contraint de plus le cadre du
graphe à être carré.
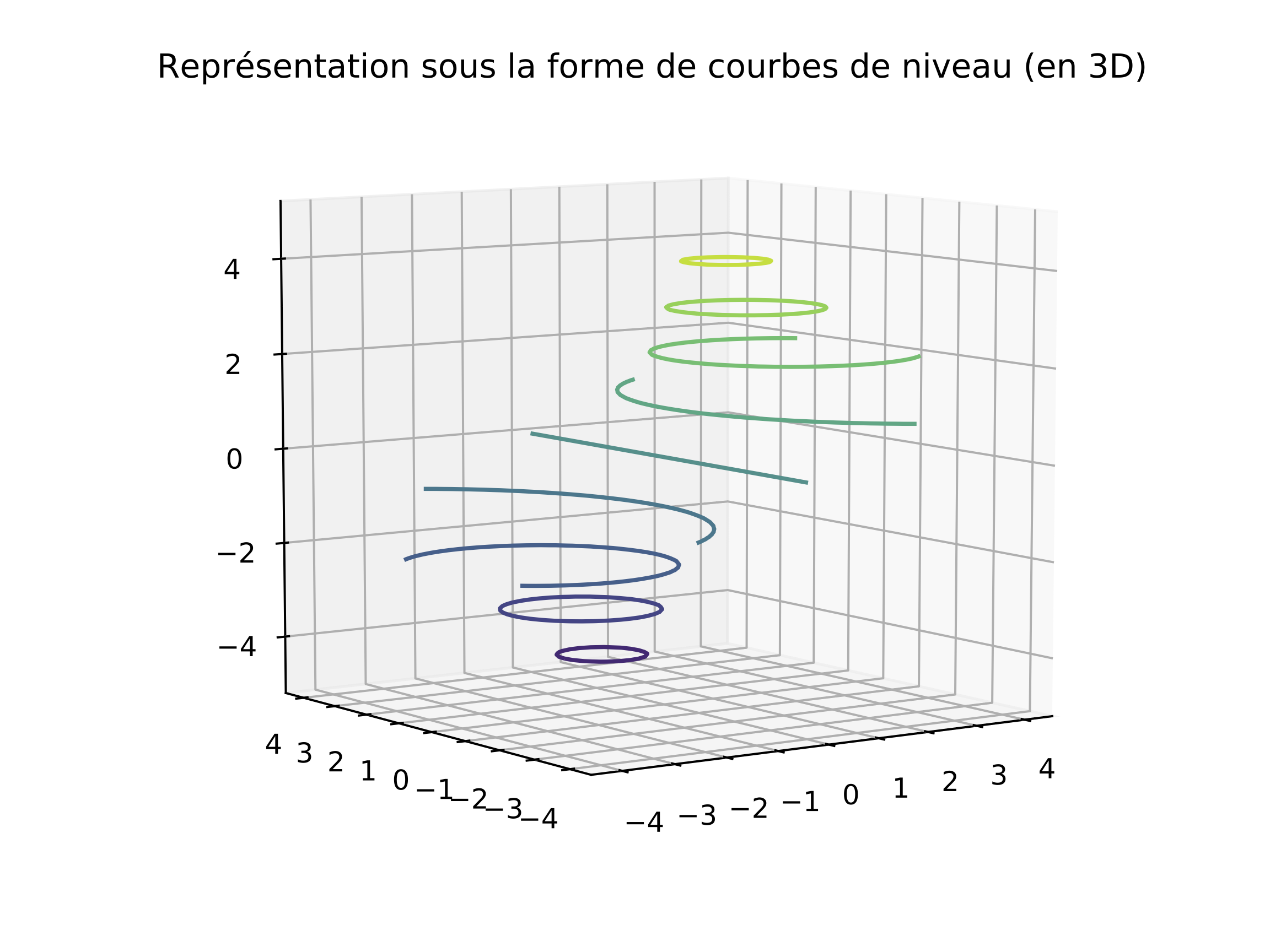
La fonction ax.contour s'applique également en trois
dimensions :
# La ligne ci-dessus permet en principe de modifier
# l'angle de vue de la représentation.
# Si vous utilisez noto, il est possible que vous deviez
# installer "ipympl" (commande: pip install ipympl) puis
# faire précéder le code de la ligne %matplotlib ipympl
# (au lieu de %matplotlib notebook)
#
import numpy as np
x = y = np.linspace(-4.,4.,41)
xv, yv = np.meshgrid(x,y,indexing='ij')
#
fv = 10*xv/(1 + xv**2 + yv**2)
#
import matplotlib.pyplot as plt
fig = plt.figure(1)
ax = plt.axes(projection='3d')
ax.contour(xv,yv,fv,9)
ax.set_title("Representation sous la forme de courbes de niveau (en 3D)")
plt.show()
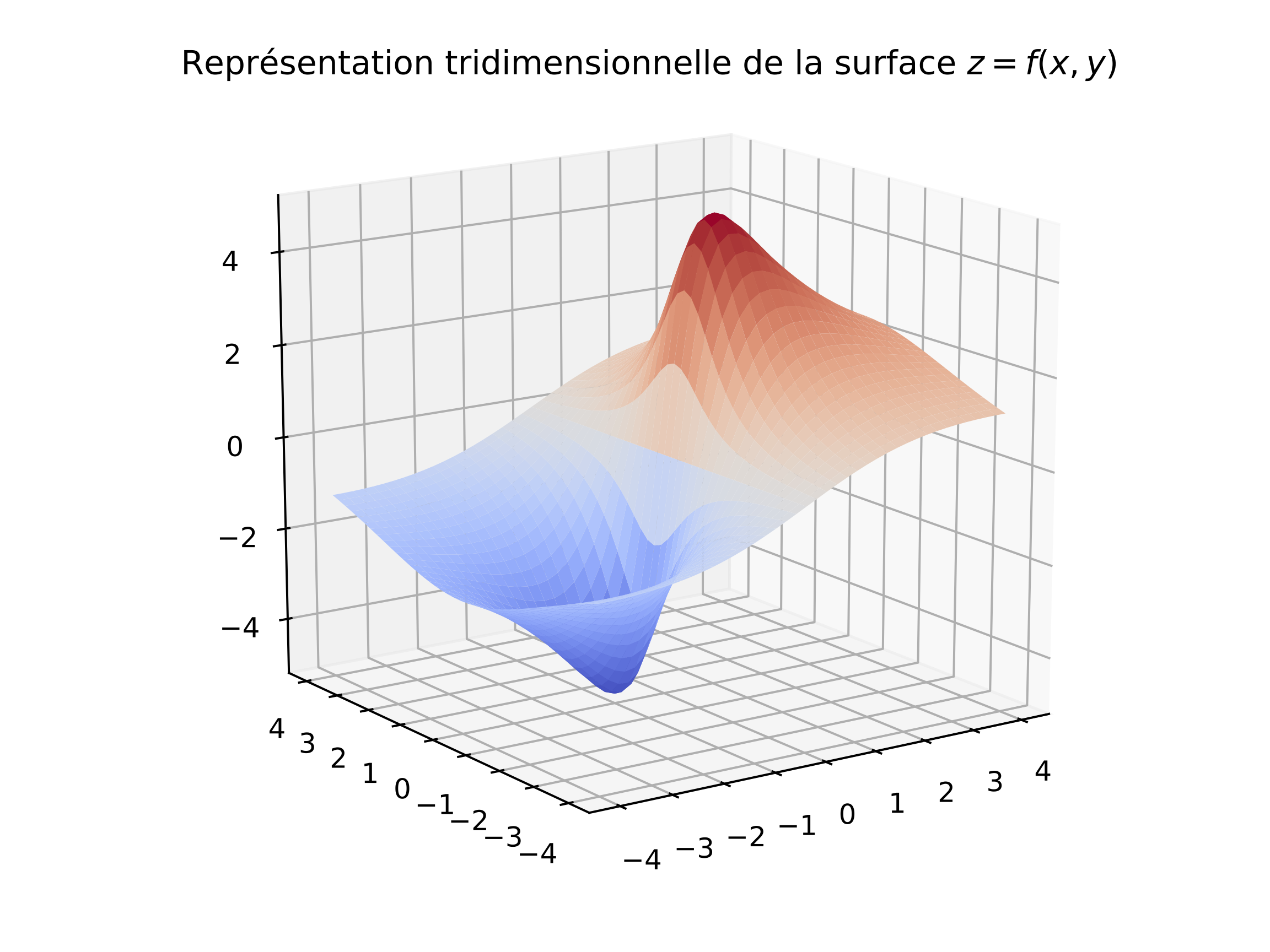
Pour visualiser le champ scalaire sous forme d'une surface en trois dimensions, les lignes suivantes s'avèrent nécessaires :
import numpy as np
x = y = np.linspace(-4.,4.,41)
xv, yv = np.meshgrid(x,y,indexing='ij')
#
fv = 10*xv/(1 + xv**2 + yv**2)
#
import matplotlib.pyplot as plt
from matplotlib import cm
fig = plt.figure(1)
ax = plt.axes(projection='3d')
ax.plot_surface(xv,yv,fv,cmap = cm.coolwarm)
ax.set_title("Représentation 3D de la surface $z=f(x,y)$")
plt.show()
La fonction ax.plot_surface utilise ici une carte des
couleurs (cmap) qui associe une couleur ''chaude'' (rouge)
aux grandes valeurs de \(f\) et une couleur ''froide'' (bleue) aux
valeurs les plus petites.
Types de représentations tridimensionnelles envisageables pour un champ scalaire :
Dernière compilation: 2025-05-28 (06:27:05)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
