Exercice 02-09
Montrer que les irrationnels sont denses dans \(\mathbb{R}\).
Il s'agit de démontrer que pour deux réels quelconques \(x\lt y\), il existe toujours un irrationnel \(z\) tel que \(x\lt z\lt y\).

On pourra utiliser deux ingrédients, démontrés au cours:

on peut trouver des rationnels entre \(x\) et \(y\).

on peut utiliser l'irrationnalité de \(\sqrt{2}\) pour ''squeezer'' un irrationnel entre \(x\) et \(y\).

Soient \(x\lt y\) deux réels. Montrons qu'on peut trouver un irrationel entre \(x\) et \(y\).

On présente plusieurs façons de faire:
  1. Soit \(m\) le point milieu de \(x\) et \(y\): \(m:= \frac{x+y}{2}\). On a \(x\lt m\lt y\). Par la densité des rationnels dans \(\mathbb{R}\), on sait qu'il existe un rationnel \(r_1\in\mathbb{Q}\) tel que \(x\lt r_1\lt m\), et un rationnel \(r_2\in\mathbb{Q}\) tel que \(m\lt r_2\lt y\):
    Soit ensuite \(n\in \mathbb{N}^*\) tel que \(\frac{\sqrt{2}}{n}\lt r_2-r_1\) (un tel entier existe, puisque \(\mathbb{N}\) n'est pas majoré). Considérons alors \[z:= r_1+\frac{\sqrt{2}}{n}\,.\]
    Le nombre \(z\) est irrationnel (car s'il était rationnel alors \(\sqrt{2}=n(z-r_1)\) serait rationnel aussi), et \(x\lt z\lt y\).
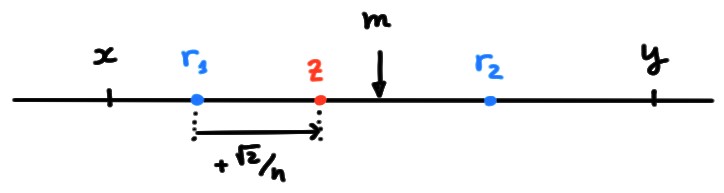
  2. Autre façon de faire: Posons \(x'=x+\sqrt{2}\), \(y'=y+\sqrt{2}\). Puisque les rationnels sont denses dans \(\mathbb{R}\), il existe un rationnel \(r\) tel que \(x'\lt r\lt y'\). Ceci implique que \(x\lt r-\sqrt{2}\lt y\). Or \(z=r-\sqrt{2}\) est irrationnel (car s'il était rationnel, alors \(\sqrt{2}=r-z\) serait rationnel aussi).
  3. Posons \(x'=x/\sqrt{2}\), \(y'=y/\sqrt{2}\). Puisque les rationnels sont denses dans \(\mathbb{R}\), il existe un rationnel \(r\) tel que \(x'\lt r\lt y'\). Ceci implique que \(x\lt \sqrt{2}r\lt y\). Or \(z=\sqrt{2}r\) est irrationnel (car s'il était rationnel, alors \(\sqrt{2}=z/r\) serait rationnel aussi).