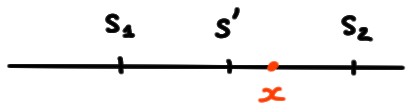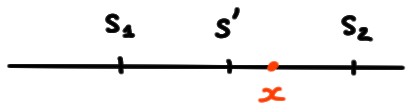En mathématiques, pour montrer qu'il existe un unique objet
satisfaisant une certaine propriété, on peut procéder par
l'absurde, c'est-à-dire qu'on montre que s'il y en avait deux, alors
cela mènerait à une contradiction.
Soit \(A\subset \mathbb{R}\) un ensemble non-vide majoré.
Pour commencer...
Supposons que \(A\) possède deux supremums, et nommons-les:
\(s_1\) et \(s_2\).
Si ces supremums sont distincts, \(s_1\neq s_2\),
alors il y en a un qui est plus grand que l'autre. Sans
perte de généralité, supposons que \(s_1\lt s_2\).
Pour la suite, un dessin peut s'avérer utile pour voir comment on arrive à une
contradiction!
Supposons qu'il existe deux supremums pour un même ensemble \(A\), notés \(s_1\)
et \(s_2\). Pour montrer que \(s_1=s_2\), on va supposer qu'ils sont différents
et obtenir une contradiction.
Supposons donc qu'ils sont différents, par exemple que \(s_1\lt s_2\).
Considérons un point intermédiaire quelconque entre \(s_1\) et \(s_2\).
Pour fixer les idées, prenons
le point milieu de \(s_1\) et \(s_2\):
\(s':= \frac{s_1+s_2}{2}\). Comme \(s_2=\sup A\), c'est le plus petit
majorant, donc il existe un \(x\in A\)
tel que \(s'\leqslant x\leqslant s_2\). Mais, comme \(s'\gt s_1\),
on a que \(x\gt s_1\), et donc \(s_1\) ne majore pas \(A\), et donc ne
peut pas être le supremum de \(A\), une contradiction.
Remarquons qu'on a pris le point milieu, mais d'autres choix sont possibles!
