- \(D(f)=\mathbb{R}\). \(f\) est paire parce que les fonctions \(x^4,\cos\) et \(\sin^2\) sont paires. \(f\) n'est pas périodique (à cause du terme \(x^4\)).
- \(D(f)=\mathbb{R}\). \(\sin\left(\frac{1}{2}x\right)\) est impair et \(4\pi\)-périodique; \(\cos\left(\frac{1}{3}x\right)\) est pair et \(6\pi\)-périodique. Ainsi \(f\) est impaire et \(12\pi\)-périodique.
- La fonction \(\tan(3x)\) n'est pas définie pour \(x \in \left\{\frac{\pi }{6}+k\cdot \frac{\pi }{3}: k\in \mathbb{Z}\right\}\), donc \[D(f)=\mathbb{R}\left\backslash \left\{\frac{\pi }{6}+k\cdot \frac{\pi }{3}: k\in \mathbb{Z}\right\}\right..\] \(\tan(3x)\) est \(\frac{\pi}{3}\)-périodique et impaire. \(\cos(\pi x)\) est \(2\)-périodique et paire. Donc \(f\) n'est ni paire ni impaire. De plus, \(f\) n'est pas périodique car \(\dfrac{\pi/3}{2} \notin \mathbb{Q}\).
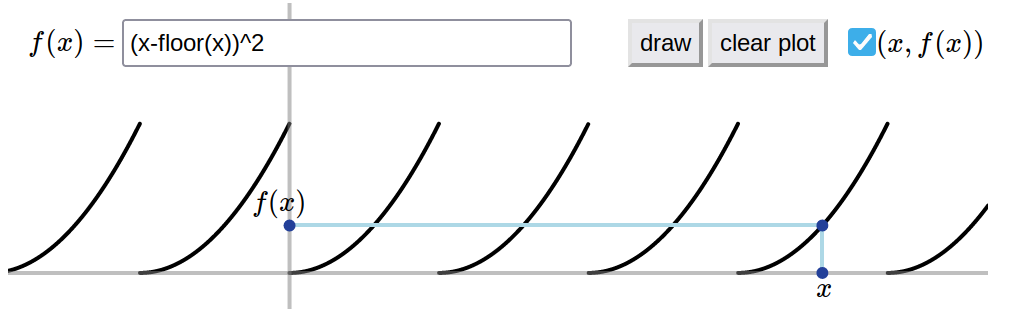
- \(D(f)=\mathbb{R}\).
Remarquons que \(f(1/3)=(-\frac13-0)^2=1/9\) et
\(f(-1/3)=(-\frac13-(-1))^2=4/9\), donc
\(f\) n'est ni paire, ni impaire.
Montrons que \(f\) est \(1\)-périodique.
En effet, pour tout réel \(x\), il existe un réel \(\alpha(x)\in [0,1[\), appelé
partie fractionnaire de \(x\), tel que
\[
x=\lfloor x\rfloor +\alpha(x)\,.
\]
(En mots: tout réel \(x\) est la somme de sa partie entière
\(\lfloor x \rfloor\) et de sa partie fractionnaire \(\alpha(x)\).)
Clairement, \(\alpha(x)\) est périodique, de période \(1\): \(\alpha(x\pm 1)=\alpha(x)\): on ne change pas la partie fractionnaire d'un réel si on le décale de \(1\) unité vers la droite/gauche. (Par exemple, si \(x=\pi=3.141529\dots\), alors \(\alpha(x)=0.141529\dots\), et donc \(x+1=4.141529\dots\), qui satisfait \(\alpha(x+1)=0.141529\dots=\alpha(x)\).) Et \(1\) est le plus petit réel \(t\gt 0\) avec cette propriété.
Ceci montre que la fonction \(x-\lfloor x \rfloor=\alpha(x)\) est périodique, de période \(1\). Ceci implique que \(f(x)=\alpha(x)^2\) est aussi de période \(1\). En effet, si \(f\) était \(t\)-périodique avec \(t\lt 1\), le fait que \(\alpha(x)\geqslant 0\) implique que \(\alpha(x)=\sqrt{f(x)}\) serait aussi \(t\)-périodique.