Exercice 08-05
(Périodicité)
- Si \(f\) est périodique, sa période est-elle toujours définie?
- Si \(f\) est périodique, montrer que \(|f|\) est aussi périodique.
La période de \(|f|\) (si elle est définie) est-elle égale à celle de \(f\)?
- Si \(|f|\) est périodique, est-ce que \(f\) est aussi périodique?
- Non. En effet, une fonction
constante est \(t\)-périodique pour tout \(t>0\) mais elle n'a pas de période au
sens strict (il n'existe pas de plus petit \(t>0\) tel que \(f\) soit
\(t\)-périodique).
- \(|f|\) est périodique car, pour tout \(x\in \mathbb{R}\),
\(|f(x+t)|=|f(x)|\), où \(t\) est une période de \(f\).
Mais la période de \(|f|\) n'est pas forcément égale à celle de \(f\).
Par exemple, \(\sin(x)\) a période \(2\pi\), alors que \(|\sin(x)|\) a
période \(\pi\).
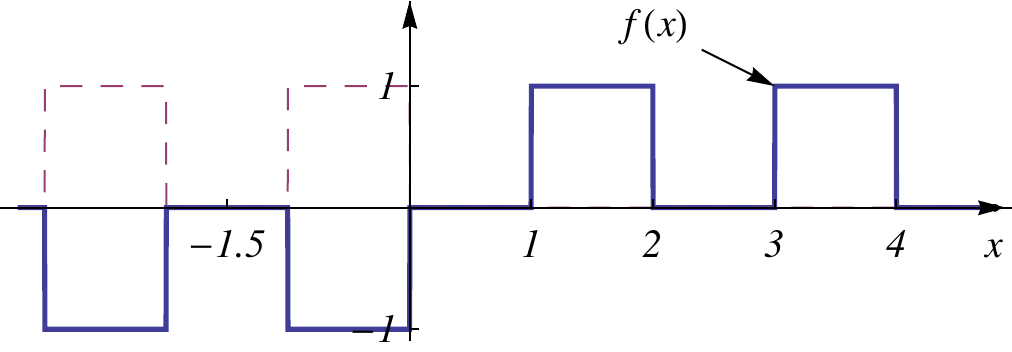
- Non. Par exemple:
Ici, \(f\) n'est manifestement pas périodique, alors que \(|f|\) est
\(2\)-périodique.