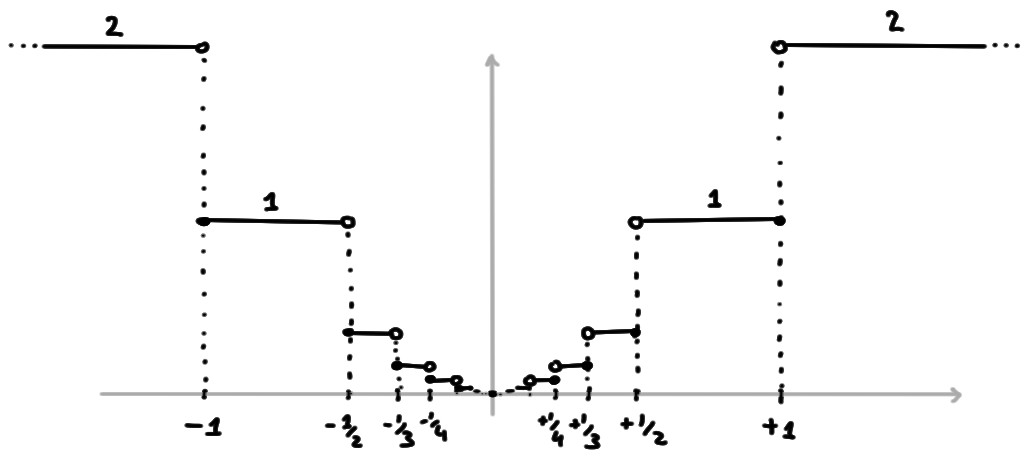
Pour commencer.
Faire un croquis, en plaçant quelques ensembles
\[J_n:=[-\tfrac{1}{n},-\tfrac{1}{n+1}[
\,\,\cup\,\, ]\tfrac{1}{n+1},\tfrac{1}{n}]\,,\]
et la valeur que \(f\) prend sur ces ensembles.
Avec un dessin raisonnable, on verra rapidement les points
\(x\neq 0\) où \(f\) est dérivable et où elle ne l'est pas.
Le point délicat.
Cette fonction est discontinue en tout point \(x\) de la forme
\(\pm\frac{1}{n}\), elle n'est donc pas non plus dérivable en ces points. En
tout point \(x\neq 0\) qui n'est pas de cette forme, elle est dérivable et sa
dérivée est nulle. Il reste à voir en \(x=0\). Pour ce faire,
posons
\[J_n:=[-\tfrac{1}{n},-\tfrac{1}{n+1}[
\,\,\cup\,\, ]\tfrac{1}{n+1},\tfrac{1}{n}]\,.\]
Remarquons que si \(x\in J_n\), alors
\[ \frac{1}{n+1}\lt |x|\leqslant \frac{1}{n}
\]
On a donc, pour tout \(x\in J_n\),
\[
\left|\frac{f(x)-f(0)}{x-0}\right|
=\frac{1/n^2}{|x|}\leqslant \frac{1/n^2}{1/(n+1)}=\frac{n+1}{n^2}\,.
\]
Cette dernière tend vers zéro lorsque \(n\to\infty\).
En prenant la limite \(x\to 0\), \(x\) traverse des ensembles \(J_n\) avec
des \(n\) de plus en plus grands, donc par le théorème des deux gendarmes,
\[
\lim_{x\to 0}\frac{f(x)-f(0)}{x-0}=0\,.
\]
Donc \(f\) est dérivable en \(x=0\), et sa dérivée en ce point est nulle.