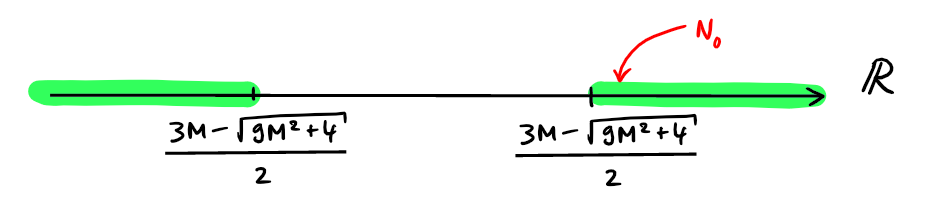1.3 Suites tendant vers l'infini
On dit qu'une suite tend vers l'infini si pour n'importe quel nombre \(M\), les
termes de la suite deviennent plus grand que \(M\) à partir d'un certain indice.
Voici la définition formelle.
Une suite \((a_n)\)
- tend vers \(+\infty\) si pour tout \(M\gt 0\) il existe
\(N_0\in \mathbb{N}^*\) tel que \(a_n\geqslant M\) pour tout \(n\geqslant N_0\). On écrit
\(\lim_{n\rightarrow\infty} a_n=+\infty\), ou \(a_n \rightarrow +\infty\).
- tend vers \(-\infty\) si pour tout \(m\lt 0\) il existe
\(N_0\in \mathbb{N}^*\) tel que \(a_n\leqslant m\) pour tout \(n\geqslant N_0\). On écrit
\(\lim_{n\rightarrow\infty} a_n=-\infty\), ou \(a_n \rightarrow -\infty\).
On dit aussi que la suite diverge vers l'infini.
Il faut penser de \(M\) comme un ''seuil''. Une suite tendant vers \(+\infty\) va,
au bout d'un moment, dépasser et rester au dessus de n'importe quel seuil.
L'indice \(N_0\) à partir duquel elle dépasse seuil dépend de la valeur
de \(M\).
Une suite \((a_n)\) tend vers \(-\infty\) si pour tout \(m \lt 0\) il
existe \(N_0\in \mathbb{N}^*\) tel que \(a_n\leqslant m\) pour tout \(n\geqslant N_0\). On écrit
\(\lim_{n\rightarrow\infty} a_n=-\infty\), ou \(a_n \rightarrow -\infty\).
Pour pouvoir facilement parler du comportement d'une suite lorsque l'indice
\(n\) devient de plus en plus grand, il est pratique d'introduire la
terminologie suivante: étant donné \(N_0\in \mathbb{N}^*\), l'ensemble \(\{n\in \mathbb{N}:
n\geqslant N_0\}\) est appelé un voisinage de l'infini.
La définition de tendre vers l'infini devient donc: \(a_n\rightarrow \infty\) si
pour tout \(M\gt 0\), il existe un voisinage de l'infini tel que \(a_n\geqslant M\)
pour des indices \(n\) dans ce voisinage de l'infini.
Exemples:
- \(\{n\in \mathbb{N} \ : \ n\geqslant 173\}\) est un voisinage de l'infini.
- \(\{n\in \mathbb{N} \ : \ (n-7)^2\gt 4\}\) contient un voisinage de l'infini.
- \(\{2n \ : \ n\in \mathbb{N} \}\) ne contient pas un voisinage de l'infini.
Exemple:
Soit \(a_n=\frac{n^2-1}{3n}\). Montrons que \(a_n\rightarrow \infty\).
Étant donné un \(M\gt 0\), il nous faut montrer qu'il existe \(N_0\) tel que
\(a_n\geqslant M\) pour tout \(n\geqslant N_0\). On a
\[\begin{aligned}
a_n\geqslant M &\iff \frac{n^2-1}{3n}\geqslant M\\
&\iff n^2-1\geqslant 3Mn\\
&\iff n^2-3Mn-1\geqslant 0\\
&\iff n\in \left]-\infty,
\frac{3M-\sqrt{9M^2+4}}{2}\right]\cup\left[\frac{3M+\sqrt{9M^2+4}}{2},
\infty\right[.
\end{aligned}\]
Si on choisit \(N_0\in \left[\frac{3M+\sqrt{9M^2+4}}{2}, \infty\right[\), on
aura \(a_n\geqslant M\) pour tout \(n\geqslant N_0\), par les équivalences au-dessus.
On peut donc par exemple prendre
\[N_0= \left\lceil \frac{3M+\sqrt{9M^2+4}}{2} \right\rceil,\]
le nombre réel \(\frac{3M+\sqrt{9M^2+4}}{2}\) arrondi vers le haut.
Exemple:
Soit \(\alpha \gt 0\) et \(a_n = \alpha n\). On va montrer que
\(a_n \rightarrow \infty\).
Etant donné \(M \gt 0\), il faut donner un \(N_0\) tel que \(a_n \gt M\)
pour tout \(n \geqslant N_0\). Or \(\alpha n \gt M \Leftrightarrow n \gt
\frac{M}{\alpha}\).
On choisit donc n'importe quel entier \(N_0 \gt \frac{M}{\alpha}\), il sera tel
que
\[n \geqslant N_0 \Rightarrow n \gt \frac{M}{\alpha} \Rightarrow a_n \gt M.\]
Exemple:
Montrons que \(a_n = \sqrt{n}\) tend vers l'infini.
Etant donné \(M \gt 0\), il faut donner un \(N_0\) tel que \(a_n \gt M\)
pour tout \(n \geqslant N_0\). Or \(\sqrt{n} \gt M \Leftrightarrow n \gt M^2.\)
On choisit donc n'importe quel entier \(N_0 \gt M^2\), il sera tel que
\[n \geqslant N_0 \Rightarrow a_n \gt M.\]
Remarque:
On a montré auparavant que \(a_n = \sqrt{n}\) n'est pas majorée:
\[\forall M \gt 0 \; \exists N \in \mathbb{N}^* \text{ tel que } a_N \gt M.\]
Dans l'exemple ci-dessus, on
vient de montrer que \(a_n = \sqrt{n}\) tend vers l'infini:
\[\forall M \gt 0 \; \exists N \in \mathbb{N}^* \text{ tel que }
n \geqslant N \Rightarrow a_n \gt M.\]
Ces deux affirmations ne sont bien sûr
pas équivalentes: si une suite \(a_n\) tend vers
l'infini, alors pour tout candidat majorant \(M \gt 0 \) qu'on nous propose,
il existe un seuil \(N \) à partir duquel tous les termes de la suite
dépassent
ce \(M\). A plus forte raison, on peut exhiber un terme de la suite qui dépasse
\(M\), ce qui montre que la suite n'est pas majorée. La réciproque est fausse:
par exemple, la suite \((-2)^n\) n'est pas majorée, mais elle ne tend pas
vers l'infini: elle admet une infinité de termes négatifs.
Une suite non majorée ne tend donc pas nécessairement vers l'infini,
mais ce sera le cas si une condition supplémentaire est vérifiée:
si une suite \(a_n\) est croissante et non majorée, alors elle tend vers
l'infini (ce résultat sera prouvé dans un exercice facultatif).
Théorème:[Théorème du chien méchant]
Soit \((a_n)\) une suite.
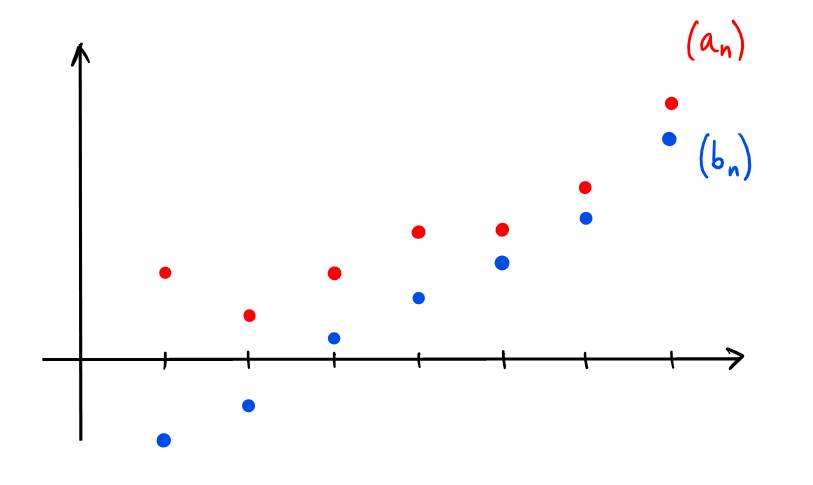
- Si \((b_n)\) est une autre suite telle que \(a_n\geqslant
b_n\) pour tout \(n\), et \(b_n \rightarrow +\infty\), alors \(a_n\rightarrow
+\infty\).
- Si \((c_n)\) est une autre suite telle que \(a_n\leqslant
c_n\) pour tout \(n\), et \(c_n \rightarrow -\infty\), alors \(a_n\rightarrow
-\infty\).
Preuve:
On démontre la première affirmation.
Supposons que \(a_n\geqslant b_n\) pour tout \(n\), et que \(b_n\to+\infty\).
Fixons \(M\gt 0\). Comme \(b_n\to+\infty\), on sait qu'il existe \(N_0\) tel que
\[
b_n\geqslant M\qquad \forall n \geqslant N_0\,.
\]
Puisque \(a_n\geqslant b_n\), ceci implique donc
\[
a_n\geqslant M\qquad \forall n \geqslant N_0\,.
\]
On a donc montré que \(a_n\to+\infty\).
Si la condition \(a_n\geqslant b_n\) n'est vraie qu'à partir d'un certain indice, on a toujours la même conclusion.
On a un théorème analogue dans le cas de \(-\infty\).
Exemple:
Reprenons l'exemple ci-dessus.
On a \(a_n=\frac{n^2-1}{3n}\geqslant \frac{n^2-3n}{3n}=\frac{n}{3}-1=:b_n\) pour
tout \(n\in \mathbb{N}^*\).
Or, \(b_n\rightarrow \infty\) (en effet: pour \(M\gt 0\), \(\frac{n}{3}-1\geqslant M
\iff n\geqslant 3M+3\), donc en prenant un entier \(N_0\geqslant 3M+3\), on a \(b_n\geqslant
M\) pour tout \(n\geqslant N_0\)). Par le théorème du chien méchant, on a donc aussi
\(a_n\rightarrow \infty\).