Analyse B (MAN)

On considère maintenant la suite \((S_n)_{n\geqslant 0}\) définie par \[\begin{aligned} S_0 &:=1\\ S_1 &:=1+r\\ S_2 &:=1+r+r^2\\ \vdots\\ S_n&:=1+r+r^2+\cdots+r^n\\ \vdots \end{aligned}\]

Sur l'animation suivante, on observe le comportement de la suite \((S_n)_{n\geqslant 0}\), en fonction de \(r\):

Preuve:

Si \(r\geqslant 1\), \(S_n=1+r+r^2+\cdots+r^n\geqslant 1+1+1+\cdots+1=n+1\rightarrow +\infty\), donc \(S_n\rightarrow +\infty\) par le théorème du chien méchant.

Si \(r\lt 1\), on a \[\begin{aligned} S_n&=1+r+r^2+\cdots+r^n\\ rS_n&=r+r^2+r^3+\cdots+r^{n+1}, \end{aligned}\] et donc \(S_n-rS_n=S_n(1-r)=1-r^{n+1}\). On obtient \[S_n=\frac{1-r^{n+1}}{1-r}.\] En vue du lemme précédent, si \(-1\lt r\lt 1\), on a \(\lim_{n\rightarrow \infty} S_n=\frac{1}{1-r}\), et si \(r\leqslant -1\), \(S_n\) n'a pas de limite.

On voit donc que pour \(|r|\lt 1\), la somme infinie \(1+r+r^2+r^3+\cdots\) converge.

La suite \((S_n)\) au-dessus est appelée la suite des sommes partielles.

Exemples:

On évalue la somme infinie \(1-0.7+0.7^2-0.7^3+0.7^4- \cdots \) en utilisant la série géométrique de raison \(-0.7\): \[1-0.7+0.7^2-0.7^3+ \cdots =1+(-0.7)+(-0.7)^2+(-0.7)^3+\cdots=\frac{1}{1-(-0.7)}=\frac{10}{17}.\]
On évalue la somme infinie \(\frac{1}{2}+\left(\frac{1}{2}\right)^2+ \left(\frac{1}{2}\right)^3 + \cdots \) en utilisant la série géométrique de raison \(\frac{1}{2}\): \[\frac{1}{2}+\left(\frac{1}{2}\right)^2+ \left(\frac{1}{2}\right)^3 + \cdots = \frac{1}{2}\left[1+ \frac{1}{2}+\left(\frac{1}{2}\right)^2 + \cdots \right] =\frac{1}{2}\cdot \frac{1}{1-\frac{1}{2}}=1.\]
La somme infinie \(1+2+2^2+2^3+2^4+\cdots\) ne converge pas, puisque \(r=2\gt 1\).

Exemple: Les séries géométriques sont utiles dans plein de contextes. Voici un exemple géométrique: le flocon de von Koch.

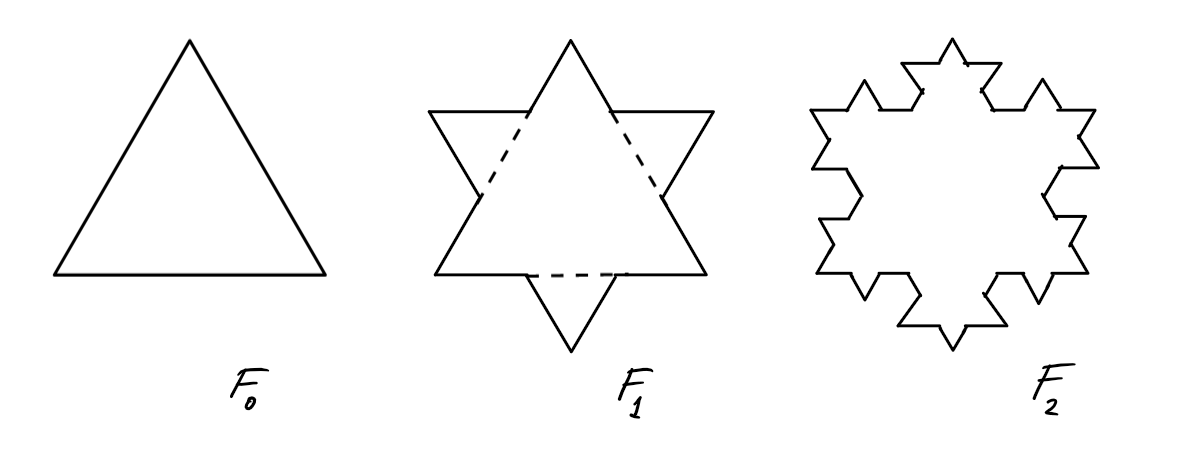
On construit les formes géométriques suivantes par récurrence, en commençant par un triangle équilatéral \(F_0\), d'aire \(1\). À chaque étape, on ''colle'' des petits triangles équilatéraux au milieu de chaque côté de la forme précédente (la longueur des côtés d'un petit triangle est un tiers de la longueur du côté à laquelle on le colle).

\[\begin{aligned} \text{ On pose } A_n&:= \text{ aire de } F_n\\ \text{ et } C_n&:= \text{ nombre de côtés de } F_n. \end{aligned}\] Ainsi, on a \[\begin{aligned} A_0&=1\\ C_0&=3\\ A_1&=A_0+C_0\cdot \frac{1}{9}=1+3\cdot\frac{1}{9}\\ C_1&=3\cdot 4\\ A_2&=A_1+C_1\cdot\left(\frac{1}{9}\right)^2=1+3\cdot\frac{1}{9}+3\cdot 4\cdot\left(\frac{1}{9}\right)^2\\ C_2&=3\cdot 4\cdot 4\\ A_3&=A_2+C_2\cdot\left(\frac{1}{9}\right)^3=1+3\cdot\frac{1}{9}+3\cdot 4\cdot\left(\frac{1}{9}\right)^2+3\cdot4\cdot 4\cdot\left(\frac{1}{9}\right)^3\\ C_3&=3\cdot 4\cdot 4\cdot 4\\ \vdots \end{aligned}\] On déduit donc les expressions \[\begin{aligned} A_n&=1+3\cdot\frac{1}{9}+3\cdot 4\cdot\left(\frac{1}{9}\right)^2+\cdots +3\cdot4^{n-1}\left(\frac{1}{9}\right)^n\\ C_n&=3\cdot 4^n \end{aligned}\] On peut réécrire \(A_n\) de la façon suivante: \[A_n=1+\frac{3}{9}\left[1+\frac{4}{9}+\left(\frac{4}{9}\right)^2+\left(\frac{4}{9}\right)^3+\cdots +\left(\frac{4}{9}\right)^{n-1}\right].\] On voit apparaître donc la série géométrique de raison \(r=\frac{4}{9}\). Ainsi, on a \[\lim_{n\rightarrow \infty} A_n =1+\frac{3}{9}\cdot\frac{1}{1-\frac{4}{9}} =\frac{8}{5}.\]

Exemple: On peut montrer que tout nombre réel dont le développement décimal est périodique est un nombre rationnel, à l'aide des séries géométriques. On prend l'exemple de \(x=1.151515151515\ldots\), mais ce qu'on va dire se généralise facilement à n'importe quel nombre à développement décimal périodique. On exprime \(x\) ainsi: \[\begin{aligned} x&=1+0.15+0.0015+0.000015+0.00000015+\cdots\\ &=1+15\cdot \frac{1}{100}+15\cdot\left(\frac{1}{100}\right)^2+15\cdot\left(\frac{1}{100}\right)^3+\cdots\\ &=1+15\cdot\frac{1}{100}\left[1+\frac{1}{100}+\left(\frac{1}{100}\right)^2+\left(\frac{1}{100}\right)^3+\cdots\right]\\ &=1+15\cdot\frac{1}{100}\cdot \frac{1}{1-\frac{1}{100}}=1+\frac{15}{99}=\frac{114}{99}. \end{aligned}\] On voit donc que \(x=\frac{114}{99}\in \mathbb{Q}\).

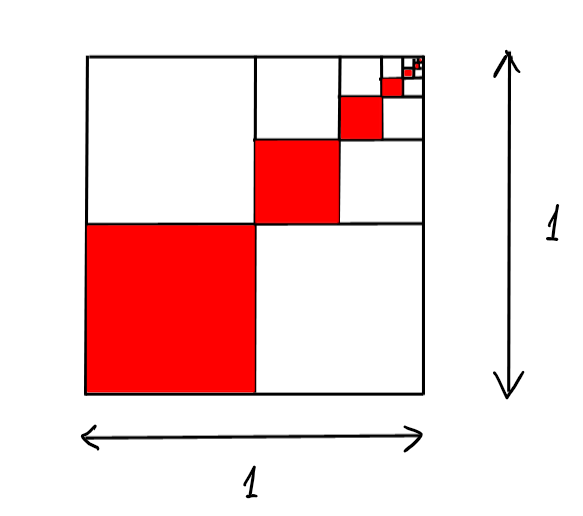
Exemple: La série géométrique suivante est une des premières à être évaluée dans l'histoire des mathématiques, par Archimède.

L'aire \(A\) indiquée ci-dessus en rouge peut être évaluée en utilisant une série géométrique. \[\begin{aligned} A&=\left(\frac{1}{2}\right)^2+\left(\frac{1}{2}\cdot \frac{1}{2}\right)^2+ \left(\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{2}\right)^2+\cdots\\ &=\frac{1}{4}+\left(\frac{1}{4}\right)^2+\left(\frac{1}{4}\right)^3+\cdots\\ &=\left[1+\frac{1}{4}+\left(\frac{1}{4}\right)^2+\left(\frac{1}{4}\right)^3+\cdots\right]-1\\ &=\frac{1}{1-\frac{1}{4}}-1=\frac{1}{3}. \end{aligned}\] La méthode de Archimède était plutôt géométrique: on constate que trois fois l'aire rouge donne l'aire du carré. On a donc \(3A=1\), d'où \(A=\frac{1}{3}\).

1.7 Séries géométriques