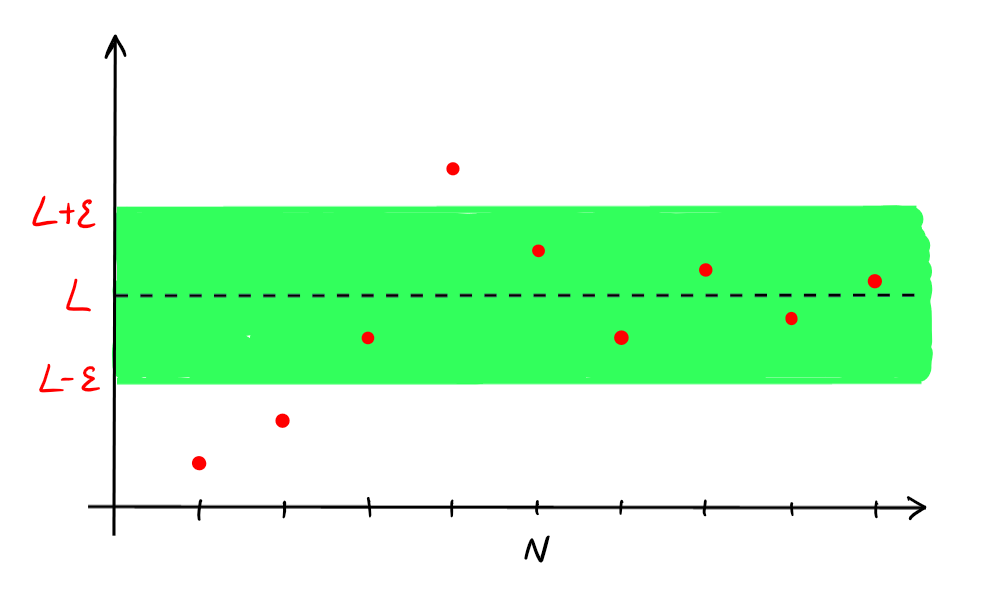
1.4 Suites convergentes
Informellement, on dit qu'une suite \((a_n)\) converge vers une limite \(L\) si
les termes de la suite deviennent arbitrairement proches de \(L\) lorsque
l'indice \(n\) est suffisamment grand. Pour rendre cette définition plus
mathématiquement précise, il nous faut une façon d'exprimer cette notion de
devenir ''arbitrairement proche'' de \(L\).
On peut exprimer la distance entre deux nombres réels \(a\) et \(b\) en utilisant la valeur absolue: \(|a-b|\). Ainsi, \(\{x\in \mathbb{R}: |a-x|\leqslant\varepsilon\}\) est l'ensemble des \(x\) qui sont à distance au plus \(\varepsilon\) de \(a\). Un tel \(x\) est dit \(\varepsilon\)-proche de \(a\), et cet ensemble est appelé l'\(\varepsilon\)-voisinage de \(a\). On a
\[\{x\in \mathbb{R}: |a-x|\leqslant\varepsilon\}=[a-\varepsilon,a+\varepsilon].\]
Pour que \((a_n)\) converge vers \(L\), on voudrait que les termes de la suite
finissent par être dans l'\(\varepsilon\)-voisinage de \(L\), pour
\(\varepsilon\) aussi petit qu'on veut.
Une suite \((a_n)\) converge vers une limite \(L\in \mathbb{R}\) si pour tout
\(\varepsilon\gt 0\), il existe \(N\in \mathbb{N}^*\) tel que pour tout \(n\geqslant N\),
\(|a_n-L|\leqslant \varepsilon\). On écrit \(\lim_{n\rightarrow \infty}a_n=L\) ou
\(a_n\rightarrow L\).
L'indice \(N\) va en général dépendre de \(\varepsilon\).
Exemples:
- Soit \(a_n=\frac{1}{n}\). On montre que \(a_n\rightarrow 0\).
Soit \(\varepsilon\gt 0\). On cherche \(N\) tel que \(|a_n-0|\leqslant\varepsilon\)
pour tout \(n\geqslant N\). On a
\(|a_n-0|=\left|\frac{1}{n}-0\right|=\frac{1}{n}\leqslant\varepsilon \iff n\geqslant
\frac{1}{\varepsilon}.\)
Donc si on prend n'importe quel \(N\) tel que \(N\geqslant \frac{1}{\varepsilon}\),
on aura bien que \(|a_n-0|\leqslant\varepsilon\) pour tout \(n\geqslant N\).
- Soit \(a_n=\frac{1}{2n+1}\). On montre que \(a_n\) ne tend pas vers
\(\frac{1}{2}\).
On a \(\left|a_n-\frac{1}{2}\right|
=\left|\frac{1}{2n+1}-\frac{1}{2}\right|
=\left|\frac{2-(2n+1)}{2(2n+1)}\right|
=\frac{2n-1}{4n+2}\),
et donc
\[\left|a_n-\frac{1}{2}\right|\leqslant\varepsilon \iff \frac{2n-1}{4n+2}
\leqslant\varepsilon \iff n\leqslant\frac{1+2\varepsilon}{2-4\varepsilon},\]
où la dernière équivalence est vraie pour \(\varepsilon\lt \frac{1}{2}\). Donc
il existe \(\varepsilon\gt 0\) (par exemple, \(\varepsilon=\frac{1}{4}\)) où on
ne peut pas trouver \(N\) tel que \(\forall n\geqslant N\), on a
\(\left|a_n-\frac{1}{2}\right|\leqslant\varepsilon\). Ceci veut dire que \(a_n
\nrightarrow\frac{1}{2}\).
-
Soit \(a_n = \frac{1}{\sqrt{n}}\). On montre que \(a_n \rightarrow 0\).
Soit \(\varepsilon \gt 0\). On veut exhiber un \(N\) tel que
\(n \geqslant N \Rightarrow \left|\frac{1}{\sqrt{n}} - 0 \right| \lt \varepsilon\).
Or
\[
\left|\frac{1}{\sqrt{n}} - 0 \right| \lt \varepsilon \Longleftrightarrow
\frac{1}{\sqrt{n}} \lt \varepsilon \Longleftrightarrow
\sqrt{n} \gt \frac{1}{\varepsilon} \Longleftrightarrow
n \gt \frac{1}{\varepsilon^2}.
\]
On choisit donc n'importe quel \(N \gt \frac{1}{\varepsilon^2}\): il sera tel
que tout \(n \geqslant N\) satisfait \(|a_n - 0| \lt \varepsilon\).
- Soit \(a_n=\frac{2n^2-1}{n^2+1}\). On montre que \(a_n\rightarrow 2\).
Soit \(\varepsilon\gt 0\). On cherche \(N\) tel que \(|a_n-2|\leqslant\varepsilon\)
pour tout \(n\geqslant N\). On a
\[|a_n-2|=\left|\frac{2n^2-1}{n^2+1}-2\right|=\left|\frac{2n^2-1}{n^2+1}-\frac{2n^2+2}{n^2+1}\right|=\left|\frac{2n^2-1-2n^2-2}{n^2+1}\right|=\frac{3}{n^2+1}.\]
Donc \(|a_n-2|\leqslant \varepsilon \iff \frac{3}{n^2+1}\leqslant \varepsilon \iff n^2\geqslant
\frac{3}{\varepsilon}-1\).
- Si \(\varepsilon\geqslant 3\), \(\frac{3}{\varepsilon}-1\leqslant 0\) et donc tout \(n\)
garantit \(|a_n-2|\leqslant \varepsilon\).
- Si \(0\lt \varepsilon \lt 3\), on a \(n^2\geqslant \frac{3}{\varepsilon}-1 \iff n\geqslant \sqrt{\frac{3}{\varepsilon}-1}\), car \(n\in\mathbb{N}^*\), et on peut donc choisir n'importe quel \(N\geqslant \sqrt{\frac{3}{\varepsilon}-1}\) pour que \(|a_n-2|\leqslant \varepsilon\) pour tout \(n\geqslant N\).
Remarque:
Une condition équivalente à \(a_n\rightarrow L\) est que tout
\(\varepsilon\)-voisinage de \(L\) contient tous les termes de la suite sauf un
nombre fini. Ceci donne une façon utile de montrer qu'une suite ne converge pas:
on montre que pour toute limite potentielle \(L\in \mathbb{R}\), il y a un
\(\varepsilon\gt 0\) tellement petit que l'\(\varepsilon\)-voisinage exclut une
infinité de termes de la suite.
Par exemple, la suite \(a_n=(-1)^n\) n'admet pas de limite car pour n'importe
quel candidat de limite \(L\), une infinité de termes de la suite ne font pas
partie de l'\(\varepsilon\)-voisinage de \(L\) pour \(\varepsilon=\frac{1}{2}\).
Donc une suite réelle peut
- converger, c'est-à-dire admettre une limite réelle \(L\)
- diverger (c'est-à-dire ne pas converger)
- en tendant vers \(-\infty\) ou \(+\infty\)
- sans tendre vers \(-\infty\) ou \(+\infty\): par exemple \((-1)^n\), \(n
\cdot (-1)^n\), ...