3.1 Limites \(x\to\pm\infty\)
On va d'abord parler des limites de fonctions lorsque \(x\) tend vers
\(+\infty\) ou \(-\infty\), car cette situation est en analogie avec les limites
de suites. Pour pouvoir étudier le comportement de \(f\) lorsque \(x\rightarrow
\pm\infty\), il faut que \(f\) soit définie en tout point aribtrairement loin de
l'origine.
- On dit que \(f\) est définie sur un voisinage de \(+\infty\) s'il
existe \(u\in \mathbb{R}\) tel que \([u,\infty[\subset D_f\).
- On dit que \(f\) est définie sur un voisinage de \(-\infty\) s'il
existe \(v\in \mathbb{R}\) tel que \(]-\infty, v]\subset D_f\).
Exemples:
-
\(\frac{1}{x}\) est définie sur \(\mathbb{R}^*\), et donc
sur un voisinage de \(+\infty\), donné par \(]0,+\infty[\),
ainsi que
sur un voisinage de \(-\infty\), donné par \(]-\infty,0[\).
- \(\tan(x)\) est définie sur \(\mathbb{R}\setminus
\{\frac{\pi}{2}+k\pi,\,k\in\mathbb{Z}\}\), et donc sur aucun voisinage de l'infini.
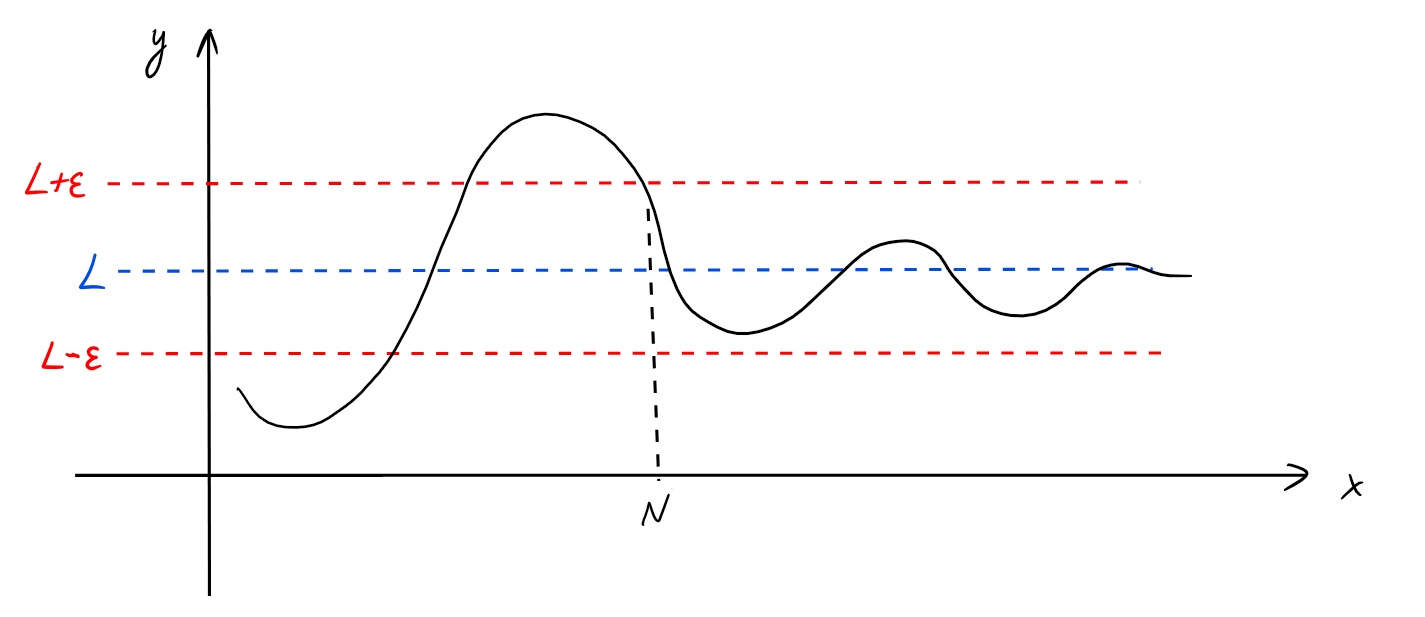
Avant de définir formellement \(\lim_{x\rightarrow +\infty} f(x)\), parlons de
l'idée intuitive derrière: \(f\) tend vers une limite \(L\) lorsque
\(x\rightarrow +\infty\) si \(f(x)\) devient arbitrairement proche de \(L\)
lorsque \(x\) est suffisamment grand.
Il faut donc que, pour \(\varepsilon\gt
0\) arbitrairement petit, on puisse trouver une valeur de \(x\) suffisamment
grande à partir de laquelle \(f(x)\) est \(\varepsilon\)-proche de \(L\).
- Soit \(f\) une fonction définie sur un voisinage de \(+\infty\), et soit
\(L\in \mathbb{R}\).
\(\displaystyle\lim_{x\rightarrow +\infty} f(x)=L\)
si \(\forall \varepsilon\gt 0\), \(\exists N\gt 0\)
tel que \(|f(x)-L|\leqslant \varepsilon\) \(\forall x\geqslant N\).
- Soit \(f\) une fonction définie sur un voisinage de \(-\infty\), et soit
\(L\in \mathbb{R}\).
\(\displaystyle\lim_{x\rightarrow -\infty} f(x)=L\) si
\(\forall \varepsilon\gt 0\), \(\exists N\lt 0\)
tel que \(|f(x)-L|\leqslant \varepsilon\) \(\forall x\leqslant N\).
Remarquons que la
valeur de \(N\) va en général dépendre de \(\varepsilon\).
Exemples:
- Soit \(f(x):=\frac{x}{3x-2}, \; D_f = \mathbb{R} \backslash\{\frac{2}{3}\}\).
Montrons que \(\displaystyle \lim_{x\rightarrow +\infty} f(x)=\frac{1}{3}\).
Soit \(\varepsilon\gt 0\). On a
\[\left|f(x)-\frac{1}{3}\right| = \left|\frac{x}{3x-2}-\frac{1}{3}\right|
= \left|\frac{2}{3(3x-2)}\right| = \frac{2}{3|3x-2|}.\]
Donc
\[
\left|f(x)-\frac{1}{3}\right| \leqslant \varepsilon
\iff \frac{2}{3|3x-2|} \leqslant \varepsilon\\
\iff |3x-2|\geqslant \frac{2}{3 \varepsilon}.
\]
Puisque on s'intéresse à \(x\rightarrow +\infty\),
on peut poser \(x \gt \frac{2}{3}\) (en effet, on cherche à trouver un voisinage
de l'infini dans lequel \(f(x)\) est \(\varepsilon\)-proche de \(\frac{1}{3}\).
Imposer une condition supplémentaire du type ''\(x\) est assez grand''
ne changera rien à l'existence d'un tel voisinage de l'infini). On a donc
\[
\left|f(x)-\frac{1}{3}\right| \leqslant \varepsilon \iff
3x-2\geqslant \frac{2}{3 \varepsilon} \iff
x \gt \frac{2}{9\varepsilon} + \frac{2}{3}.
\]
et donc on peut choisir \(N:=\frac{2}{9\varepsilon} + \frac{2}{3}\). En effet, ce \(N\)
satisfait
\[
x \gt \frac{2}{9\varepsilon} + \frac{2}{3} \Longrightarrow
\left|f(x)-\frac{1}{3}\right| \leqslant \varepsilon.
\]
On en conclut que \(\displaystyle \lim_{x\rightarrow +\infty} f(x)=\frac{1}{3}\).
- Montrons que \(\lim_{x\rightarrow -\infty} \frac{1}{x^2} = 0\).
Soit \(\varepsilon\gt 0\). On a
\[\begin{aligned}
\left|\frac{1}{x^2}-0\right|\leqslant \varepsilon
&\iff \frac{1}{x^2} \leqslant \varepsilon \\
&\iff x^2\geqslant \frac{1}{\varepsilon} \\
&\iff x\in ]-\infty, \tfrac{-1}{\sqrt{\varepsilon}}]
\cup [\tfrac{1}{\sqrt{\varepsilon}},\infty[,
\end{aligned}\]
donc si on choisit \(N\leqslant \frac{-1}{\sqrt{\varepsilon}}\), on aura que
\(\forall x\leqslant N\), \(\left|\frac{1}{x^2}-0\right|\leqslant \varepsilon\).
Etant donnée une suite \((x_n)\), en appliquant une fonction \(f\) à chaque
terme, on obtient une nouvelle suite \((f(x_n))\). On remarque que si
\(\lim_{x\rightarrow \infty} f(x)=L\), alors pour n'importe
quelle suite de nombres \((x_n)\) avec \(x_n\rightarrow \infty\), on a
\(f(x_n)\rightarrow L\). La réciproque est vraie aussi !
Théorème: [Caractérisation par les suites]
- Soit \(f\) une fonction définie sur un voisinage de \(+\infty\).
\(\displaystyle\lim_{x\rightarrow +\infty} f(x)=L \iff\) pour toute suite
\((x_n)\) telle que \(x_n\rightarrow \infty\), on a
\(\displaystyle\lim_{n\rightarrow \infty} f(x_n)=L\).
- Soit \(f\) une fonction définie sur un voisinage de \(-\infty\).
\(\displaystyle\lim_{x\rightarrow -\infty} f(x)=L \iff\)
pour toute suite \((x_n)\) telle que \(x_n\rightarrow -\infty\), on a
\(\displaystyle\lim_{n\rightarrow \infty} f(x_n)=L\).
Preuve:
Montrons la version \(x\rightarrow +\infty\) (la version \(x\rightarrow -\infty\) peut être montrée de manière analogue).
Voici la direction ''facile'': supposons d'abord que \(\lim_{x\rightarrow +\infty} f(x)=L\). Par définition, ceci veut dire que \(\forall \varepsilon\gt 0\), \(\exists N=N(\varepsilon)\gt 0\) tel que \(|f(x)-L|\leqslant \varepsilon\) \(\forall x\geqslant N\). Soit \((x_n)\) une suite telle que \(x_n\rightarrow \infty\), et soit \(\varepsilon\gt 0\). Il nous faut trouver un indice à partir duquel \(f(x_n)\) est \(\varepsilon\)-proche de \(L\).
Puisque \(x_n\rightarrow \infty\), il existe un indice \(N_0\) à partir duquel \(x_n\geqslant N(\varepsilon)\). Pour \(n\geqslant N_0\), on a alors \(x_n\gt N(\varepsilon)\) et donc \(|f(x_n)-L|\leqslant \varepsilon\). \(N_0\) est donc l'indice qu'on voulait trouver.
Pour l'autre direction, on va montrer la contraposée: si \(\lim_{x\rightarrow \infty} f(x)\neq L\), alors il existe une suite \((x_n)\) telle que \(x_n\rightarrow +\infty\), mais \(\lim_{n\rightarrow \infty} f(x_n)\neq L\). D'abord, explicitons l'assertion \(\lim_{x\rightarrow \infty} f(x)\neq L\).
\(\lim_{x\rightarrow \infty} f(x)\neq L\) veut dire: \(\exists \varepsilon\gt 0\) tel que \(\forall N\gt 0\), \(\exists x\geqslant N\) tel que \(|f(x)-L|\gt \varepsilon.\)
Supposons donc que \(\lim_{x\rightarrow \infty} f(x)\neq L\). On aimerait
construire une suite \((x_n)\) telle que \(x_n\rightarrow \infty\) et
\(\lim_{n\rightarrow \infty} f(x_n)\neq L\). On sait qu'il existe
\(\varepsilon\gt 0\) tel que \(\forall N\gt 0\), \(\exists x\geqslant N\) tel que
\(|f(x)-L|\gt \varepsilon\).
- En prenant \(N=1\) d'abord, on aura donc \(x_1\geqslant 1\) tel que \(|f(x_1)-L|\gt
\varepsilon\).
- En prenant \(N=2\), on aura \(x_2\geqslant 2\) tel que \(|f(x_2)-L|\gt \varepsilon\).
- En prenant \(N=3\), on aura \(x_3\geqslant 3\) tel que \(|f(x_3)-L|\gt \varepsilon\).
- etc.
En continuant de cette manière, on a
construit une suite \((x_n)\) telle que \(x_n\geqslant n\), et donc \(x_n\rightarrow
\infty\), et \(|f(x_n)-L|\gt \varepsilon\) \(\forall n\). Ainsi,
\(\lim_{n\rightarrow \infty} f(x_n)\neq L\) puisque \(f(x_n)\) est toujours à
distance \(\gt \varepsilon\) de \(L\), et on a donc prouvé la contraposée.
Ce théorème est surtout utile pour montrer qu'une fonction ne tend
pas vers une certaine limite \(L\in\mathbb{R}\)
lorsque \(x\rightarrow \pm\infty\): il suffit de trouver une suite \((x_n)\)
qui tend vers \(\pm\infty\) mais telle que \(f(x_n)\) ne tend pas vers \(L\).
Exemple:
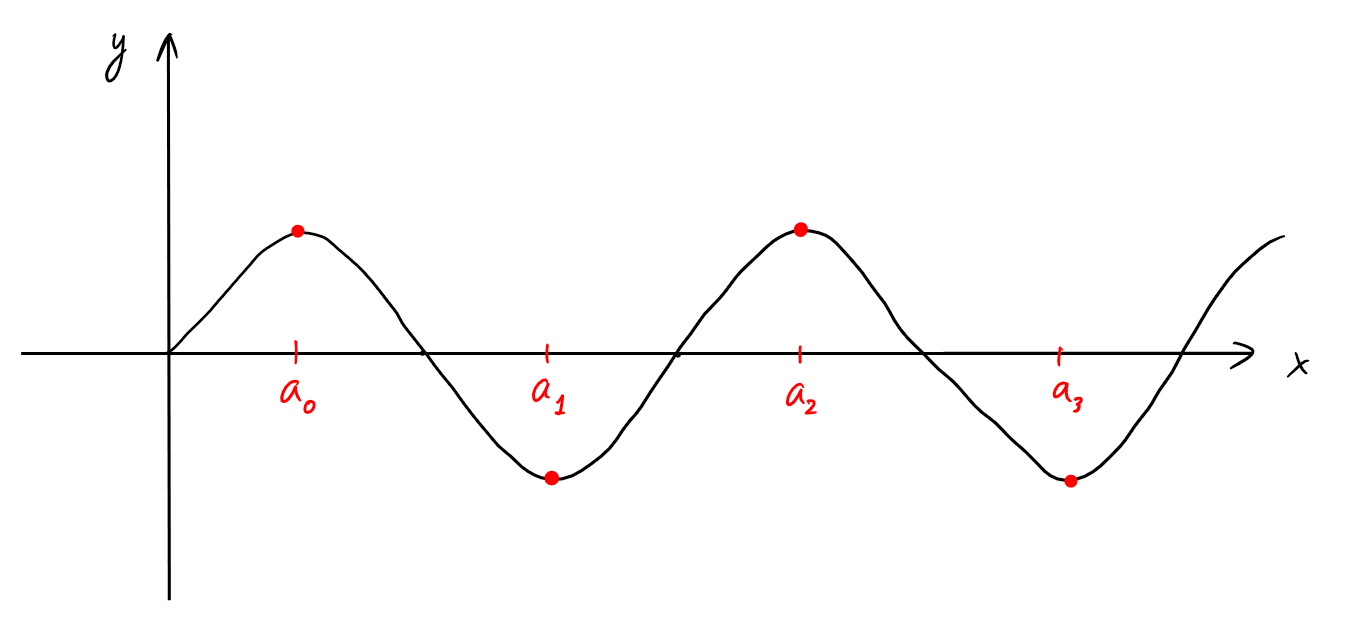
Montrons que \(\lim_{x\rightarrow \infty} \sin(x)\) n'existe pas.
Soit \((x_n)\) la suite définie par \(x_n=\frac{\pi}{2}+\pi n\).
On a bien que \(x_n+\to \infty\). Or
\(\sin(x_n)=(-1)^{n+1}\), qui n'a pas de limite lorsque \(n\to \infty\).
Le théorème ci-dessus implique que
la limite \(\lim_{x\rightarrow \infty} \sin(x)\) n'existe pas.
(Parce que si il existait \(L\in \mathbb{R}\) tel que
\(\lim_{x\rightarrow \infty} \sin(x)=L\), alors on devrait aussi avoir
\(\lim_{n\rightarrow \infty} \sin(x_n)=L\).)
Comme pour les suites, on peut définir la divergence à l'infini:
- Soit \(f\) définie sur un voisinage de \(+\infty\).
- On dit que \(\displaystyle\lim_{x\rightarrow +\infty} f(x)=+\infty\) si \(\forall M\gt 0,\) \(\exists N\) tel que \(f(x)\geqslant M\) \(\forall x\geqslant N\).
- On dit que \(\displaystyle\lim_{x\rightarrow +\infty} f(x)=-\infty\) si \(\forall M\lt 0,\) \(\exists N\) tel que \(f(x)\leqslant M\) \(\forall x\geqslant N\).
- Soit \(f\) définie sur un voisinage de \(-\infty\).
- On dit que \(\displaystyle\lim_{x\rightarrow -\infty} f(x)=+\infty\) si \(\forall M\gt 0,\) \(\exists N\) tel que \(f(x)\geqslant M\) \(\forall x\leqslant N\).
- On dit que \(\displaystyle\lim_{x\rightarrow -\infty} f(x)=-\infty\) si \(\forall M\lt 0,\) \(\exists N\) tel que \(f(x)\leqslant M\) \(\forall x\leqslant N\).
Exemples:
- Montrons que
\[
\lim_{x\rightarrow -\infty} x^3 = -\infty\,.
\]
Soit \(M \lt 0\). On a
\(x^3 \leqslant M \iff x \leqslant \sqrt[3]{M}\). On peut donc choisir par exemple
\(N := \sqrt[3]{M}\), qui satisfait \(x^3 \leqslant M\) \(\forall x \leqslant N\).
- Montrons que
\[
\lim_{x\rightarrow -\infty} x^2 = +\infty\,.
\]
Soit \(M \gt 0\). On a
\[x^2 \geqslant M \iff x \leqslant -\sqrt{M} \text{ ou } x \geqslant \sqrt{M}.\]
On peut donc choisir un
\(N \leqslant -\sqrt{M}\), il satisfait \(x^2 \geqslant M\) \(\forall x \leqslant N\).
Calculs de limites
Pour chacun des types de limite introduit ci-dessus,
toutes les propriétés énoncées pour limites de suites restent valables.
De plus, les méthodes introduites pour étudier les limites
combinées et indéterminations de suites,
s'appliquent aussi aux limites de fonctions
lorsque \(x\rightarrow \pm \infty\).
Exemple: Pour calculer
\[
\lim_{x\to \infty} \left(6x - 4x\sin(7x^2+1)\right)
=
\lim_{x\to \infty} x\left(6 - 4\sin(7x^2+1)\right)\,,
\]
on sait que \(\lim_{x\to \infty} x=\infty\) et que
pour tout \(x\), \(6-4\sin(7x^2+1)\geqslant 6-4=2\).
On a donc que
\[
\lim_{x\to \infty} \left(6x - 4x\sin(7x^2+1)\right)
=+\infty
\]
Exemple: Pour calculer
\[
\lim_{x\to-\infty}
\left(x^2-x^3\right)\,,
\]
on remarque que le terme dominant est \(x^3\), et donc on peut écrire
\[
x^2-x^3
=
\underbrace{x^3}_{\to-\infty}
\underbrace{\left(-1+\frac{1}{x}\right)}_{\to -1}\,.
\]
Comme \(-1\lt 0\), on peut conclure:
\[
\lim_{x\to-\infty}
\left(x^2-x^3\right)=-\infty\,.
\]
Ce dernier exemple montre qu'en général, dans
une limite \(x\to\pm \infty\), le comportement d'un polynôme est régi par
le terme de plus grand degré.
Lorsqu'on étudie des quotients de polynômes, on pourra mettre les termes
dominants en évidence.
Exemples:
-
\[
\lim_{x\to \infty} \frac{x^2-x^3}{4x^3+50x^2}
=\lim_{x\to \infty}
\frac{x^3\left(\frac{1}{x}-1\right)}{x^3\left(4+\frac{50}{x}\right)}
=\frac{\lim_{x\to \infty}
\left(\frac{1}{x}-1\right)}{\lim_{x\to \infty}\left(4+\frac{50}{x}\right)}
=\frac{-1}{4}
\]
-
\[\begin{aligned}
\lim_{x\to \infty} \frac{3x^2-2x+1}{5x^5+2}
&=
\lim_{x\to \infty}
\frac{x^2(3-\frac{1}{x}+\frac{1}{x^2})}{x^5(5+\frac{2}{x^5})}\\
&=\lim_{x\to \infty}
\frac{1}{x^3}\cdot
\frac{3-\frac{1}{x}+\frac{1}{x^2}}{5+\frac{2}{x^5}}\\
&=0\cdot\frac{3}{5}=0
\end{aligned}\]
-
\[
\lim_{x\to -\infty} \frac{8x^6}{x^3+4x^2+3}
=
\lim_{x\to -\infty} x^3\cdot \frac{8}{1+\frac{4}{x}+\frac{3}{x^3}}
=-\infty
\]
- Même lorsque les expressions apparaissant dans le quotient ne sont pas
exactement des polynômes,
\[\begin{aligned}
\lim_{x\to +\infty} \frac{\sqrt[4]{x^4+2x}}{\sqrt[3]{x^3+3x}}
&=\lim_{x\to +\infty}
\frac{|x|\sqrt[4]{1+\frac{2}{x^3}}}{x\sqrt{1+\frac{3}{x^2}}}\\
&= \lim_{x\to +\infty}
\frac{\sqrt[4]{1+\frac{2}{x^3}}}{\sqrt{1+\frac{3}{x^2}}}\\
&=\frac{\sqrt[4]{1+
\lim_{x\to +\infty}\frac{2}{x^3}}}{\sqrt{1+ \lim_{x\to +\infty}\frac{3}{x^2}}}\\
&=1.
\end{aligned}\]
On a utilisé le fait que \(|x|=x\) lorsque \(x\gt 0\) (ce qui est le cas puisque
\(x\to +\infty\)).
Comme on sait, l'utilisation du conjugué s'avère utile lorsqu'on a des
différences de racines:
Exemple:
\[\begin{aligned}
\lim_{x\rightarrow -\infty}&
\left(\sqrt{x^2-3x}+x\right)\\
&=\lim_{x\rightarrow -\infty}
\frac{\left(\sqrt{x^2-3x}+x\right)\left(\sqrt{x^2-3x}-x\right)}{\left(\sqrt{x^2-3x}-x\right)}\\
&= \lim_{x\rightarrow -\infty}\frac{-3x}{\left(\sqrt{x^2-3x}-x\right)}\\
&=\lim_{x\rightarrow -\infty}\frac{-3x}{\left(|x|\sqrt{1-\frac{3}{x}}-x\right)}\\
&=\lim_{x\rightarrow -\infty}\frac{-3x}{\left(-x\sqrt{1-\frac{3}{x}}-x\right)}\\
&=\lim_{x\rightarrow -\infty}\frac{3}{\left(\sqrt{1-\frac{3}{x}}+1\right)}\\
&=\frac{3}{\left(\sqrt{1-\lim_{x\rightarrow -\infty}\frac{3}{x}}+1\right)}\\
&=\frac{3}{2}.
\end{aligned}\]
On a utilisé le fait que \(|x|=-x\) lorsque \(x\lt 0\) (ce qui est le cas puisque
\(x\to -\infty\)).
Exemple:
Déterminons la valeur de \(p\in \mathbb{R}\) pour laquelle la limite
\[
\lim_{x\rightarrow +\infty} \sqrt{x^2+ax}+px
\]
est finie.
Si \(p\geqslant 0\), \(\lim_{x\rightarrow +\infty} \sqrt{x^2+ax}+px=+\infty\)
pour tout \(a\), donc on doit considérer \(p\lt 0\).
Dans ce cas, la limite est une indétermination ''\(\infty-\infty\)'', et on peut
écrire
\[\begin{aligned}
\lim_{x\rightarrow +\infty} \sqrt{x^2+ax}+px
&= \lim_{x\rightarrow +\infty} \frac{\left(\sqrt{x^2+ax}+px\right)
\left(\sqrt{x^2+ax}-px\right)}{\sqrt{x^2+ax}-px}\\
&= \lim_{x\rightarrow +\infty} \frac{(1-p^2)x^2+ax}{\sqrt{x^2+ax}-px}\\
&= \lim_{x\rightarrow +\infty} \frac{(1-p^2)x^2+ax}{|x|\sqrt{1+\frac{a}{x}}-px}\\
&= \lim_{x\rightarrow +\infty} \frac{(1-p^2)x+a}{\sqrt{1+\frac{a}{x}}-p}.
\end{aligned}\]
On voit que si \(1-p^2 \neq 0\), cette limite n'existe pas. Comme on est dans le
cas \(p\lt 0\), l'unique valeur possible est donc \(p=-1\). Dans ce cas, la
limite est égale à
\[
\lim_{x\rightarrow +\infty} \sqrt{x^2+ax}-x
=\lim_{x\rightarrow +\infty}
\frac{a}{\sqrt{1+\frac{a}{x}}+1}=\frac{a}{2}\,.
\]
Enonçons encore une version du Théorème des deux gendarmes dans le cas des
fonctions, dans le cas \(x\rightarrow \infty\)
(la version analogue avec \(x\rightarrow -\infty\) est semblable):
Théorème: [Théorème des deux gendarmes]
Soit \(f\) une fonction définie dans un voisinage de \(+\infty\).
S'il existe des fonctions \(g\) et \(h\), également définies dans un voisinage
de \(+\infty\), telles que
- \(g(x)\leqslant f(x) \leqslant h(x)\) \(\forall x\) suffisamment grand, et
- \(\lim_{x\rightarrow \infty} g(x)=\lim_{x\rightarrow \infty} h(x)=L\),
alors \(\lim_{x\rightarrow \infty} f(x)=L\).
Exemple:
Soit \(f(x)=\frac{E\left(\sqrt{x}\right)}{x}\), où \(E\) est la fonction
''partie entière''. Montrons que \(\lim_{x\rightarrow \infty} f(x)=0\).
On a \(\sqrt{x}-1\leqslant E\left(\sqrt{x}\right) \leqslant \sqrt{x}\) \(\forall x\), et
donc \(\frac{\sqrt{x}-1}{x}\leqslant \frac{E\left(\sqrt{x}\right)}{x} \leqslant
\frac{\sqrt{x}}{x}\) \(\forall x\gt 0\).
On a alors, pour \(x\gt 0\),
\[\frac{1}{\sqrt{x}}-\frac{1}{x}\leqslant f(x) \leqslant \frac{1}{\sqrt{x}}.\]
On pose \(g(x):=\frac{1}{\sqrt{x}}-\frac{1}{x}\) et
\(h(x):=\frac{1}{\sqrt{x}}\).
On a
\[
\lim_{x\rightarrow \infty}g(x)
=\lim_{x\rightarrow \infty}\frac{1}{\sqrt{x}}-\lim_{x\rightarrow
\infty}\frac{1}{x}=0-0=0\,,
\]
et \(\lim_{x\rightarrow \infty} h(x)=\lim_{x\rightarrow
\infty}\frac{1}{\sqrt{x}}=0.\) Par le Théorème des deux gendarmes, on a alors
que \(\lim_{x\rightarrow \infty} f(x)=0\).