3.5 Limites infinies en un point
On définit maintenant la divergence vers l'infini en un point.
Soit \(x_0\in\mathbb{R}\) et \(f\) une fonction définie sur un voisinage épointé de
\(x_0\).
- \(f\) tend vers \(+\infty\) lorsque \(x\rightarrow x_0\) si \(\forall M\gt
0\), \(\exists \delta\gt 0\) tel que
\[
0\lt |x-x_0|\leqslant \delta
\quad
\Longrightarrow
\quad
f(x)\geqslant M\,.\]
On écrit \(\lim_{x\rightarrow x_0}f(x)=+\infty\).
- \(f\) tend vers \(-\infty\) lorsque \(x\rightarrow x_0\) si
\(\forall M\lt 0\), \(\exists \delta\gt 0\) tel que
\[
0\lt |x-x_0|\leqslant \delta
\quad
\Longrightarrow
\quad
f(x)\leqslant M\,.
\]
On écrit \(\lim_{x\rightarrow x_0}f(x)=+\infty\).
- \(f\) tend vers \(+\infty\) lorsque \(x\rightarrow x_0^+\) si
\(\forall M\gt 0\), \(\exists \delta\gt 0\) tel que \[x_0\lt x \leqslant x_0+\delta
\quad
\Longrightarrow
\quad
f(x)\geqslant M.\]
On écrit \(\lim_{x\rightarrow x_0^+}f(x)=+\infty\).
- \(f\) tend vers \(-\infty\) lorsque \(x\rightarrow x_0^+\) si
\(\forall M\lt 0\), \(\exists \delta\gt 0\) tel que \[x_0\lt x \leqslant x_0+\delta
\quad
\Longrightarrow
\quad
f(x)\leqslant M.\]
On écrit \(\lim_{x\rightarrow x_0^+}f(x)=-\infty\).
- \(f\) tend vers \(+\infty\) lorsque \(x\rightarrow x_0^-\) si
\(\forall M\gt 0\), \(\exists \delta\gt 0\) tel que \[
x_0-\delta\leqslant x \lt x_0
\quad
\Longrightarrow
\quad
f(x)\geqslant M.\]
On écrit \(\lim_{x\rightarrow x_0^-}f(x)=+\infty\).
- \(f\) tend vers \(-\infty\) lorsque \(x\rightarrow x_0^-\) si
\(\forall M\lt 0\), \(\exists \delta\gt 0\) tel que \[
x_0-\delta\leqslant x \lt x_0
\quad
\Longrightarrow
\quad
f(x)\leqslant M.\]
On écrit \(\lim_{x\rightarrow x_0^-}f(x)=-\infty\).
On définit les limites latérales infinies de manière analogue. Par exemple,
\(\lim_{x\rightarrow x_0^+}f(x)=+\infty\) \(\iff\) \(\forall M\gt 0\), \(\exists \delta\gt 0\) tel que \(x_0\lt x\leqslant x_0+\delta \Longrightarrow f(x)\geqslant M.\)
Comme avant, une limite infinie en un point \(x_0\) ne dit rien sur la valeur de \(f\) en \(x_0\).
Exemples:
-
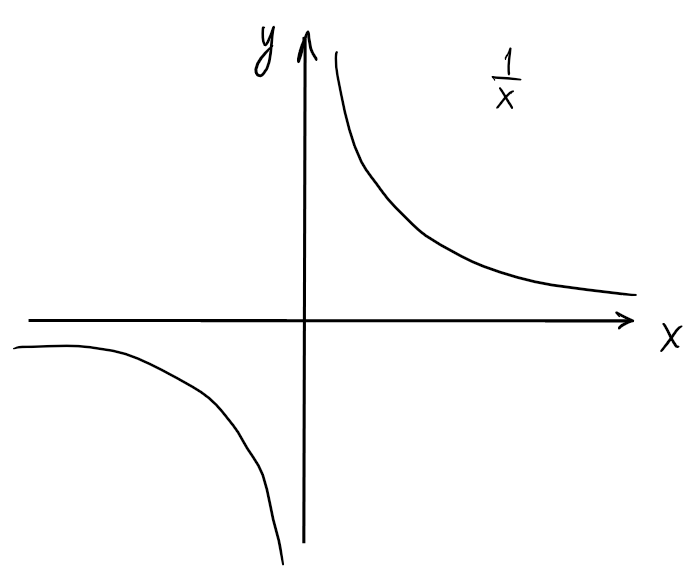
On a \(\lim_{x\rightarrow 0^+}\frac{1}{x}=+\infty\) et \(\lim_{x\rightarrow 0^-}\frac{1}{x}=-\infty\), mais \(\lim_{x\rightarrow 0}\frac{1}{x}\) ne tend pas vers \(\pm\infty\).
Montrons que \(\lim_{x\rightarrow 0^-}\frac{1}{x}=-\infty\).
Soit \(M \lt 0\). Pour \(x \lt 0\),
\[\frac{1}{x} \leqslant M \; \Leftrightarrow \; x \geqslant \frac{1}{M}.\]
On pose \(\delta = \frac{-1}{M}\); on a \(\delta \gt 0\) et \(\frac{1}{x} \leqslant M \)
pour tout \(x \in [-\delta, 0[\). On a donc bien que
\(\lim_{x\rightarrow 0^-}\frac{1}{x}=-\infty\).
-
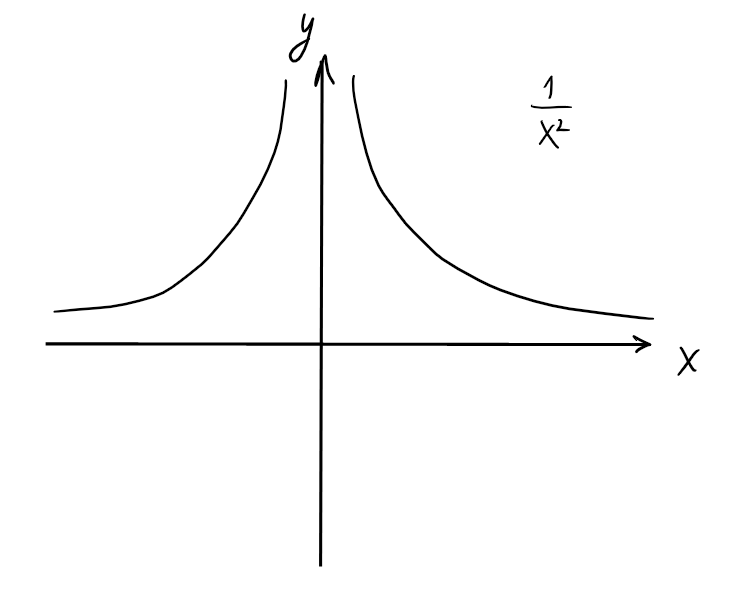
On a \(\lim_{x\rightarrow 0}\frac{1}{x^2}=+\infty\).
- Montrons que \(\lim_{x\rightarrow 1}\frac{1}{(x-1)^2}=+\infty\).
Soit \(M \gt 0\). Pour \(x \neq 1\),
\[\frac{1}{(x-1)^2} \geqslant M \; \Leftrightarrow \; (x-1)^2 \leqslant \frac{1}{M}
\; \Leftrightarrow \; |x-1| \leqslant \frac{1}{\sqrt{M}}.\]
On prend \(\delta = \frac{1}{\sqrt{M}}\) (ou n'importe quelle valeur dans \(]0, \frac{1}{\sqrt{M}}]\)). On a alors
\[0 \lt |x-1| \leqslant \delta \; \Rightarrow \; |x-1| \leqslant\frac{1}{\sqrt{M}}
\Rightarrow \frac{1}{(x-1)^2} \geqslant M.\]
Donc \(\lim_{x\rightarrow 1}\frac{1}{(x-1)^2}=+\infty\).
Les propriétés habituelles sont vérifiées pour les limites infinies en un point.
Exemples:
- Considérons
\[
\lim_{x\to -2^+}\frac{x^2+3x+1}{x^2-3x-10}\,.
\]
Dans la limite \(x\to -2^+\), le numérateur tend vers \(-1\) et
le dénominateur vers zéro \(0\).
Donc le quotient ne peut pas avoir de limite finie, et pour comprendre son
comportement il faut regarder de plus près le signe du dénominateur à son
approche de zéro.
En écrivant
\[
\frac{x^2+3x+1}{x^2-3x-10}
=
\frac{x^2+3x+1}{(x-5)(x+2)}
=
\frac{x^2+3x+1}{x-5}
\cdot
\frac{1}{x+2}\,,
\]
on a extrait le terme qui pose problème:
en posant \(y=x+2\), \(x\to -2^+\) implique \(y\to 0^+\), et donc
\[
\lim_{x\to -2^+}
\frac{1}{x+2}
=
\lim_{y\to 0^+}
\frac{1}{y}
=+\infty\,.
\]
D'autre part,
\[
\lim_{x\to -2^+}
\frac{x^2+3x+1}{x-5}
=\frac{-1}{-7}=\frac{1}{7}\,.
\]
Puisque \(\frac{1}{7}\gt 0\), on peut conclure:
\[
\lim_{x\to -2^+}
\frac{x^2+3x+1}{x^2-3x-10}
=
\lim_{x\to -2^+}
\frac{x^2+3x+1}{x-5}
\cdot
\frac{1}{x+2}
=+\infty
\]
- Considérons
\[
\lim_{x\rightarrow -1}
\frac{9-2x\sin\left(\frac{1}{x+1}\right)}{(x+1)^2}\,.
\]
Puisque
\[
\lim_{x\rightarrow -1}\frac{1}{(x+1)^2}=+\infty\,,
\]
et puisque \(9-2x\sin\left(\frac{1}{x+1}\right)\geqslant 7\gt 0\)
sur un voisinage épointé de \(-1\), on conclut que
\[
\lim_{x\rightarrow -1}
\frac{9-2x\sin\left(\frac{1}{x+1}\right)}{(x+1)^2}=+\infty\,.
\]