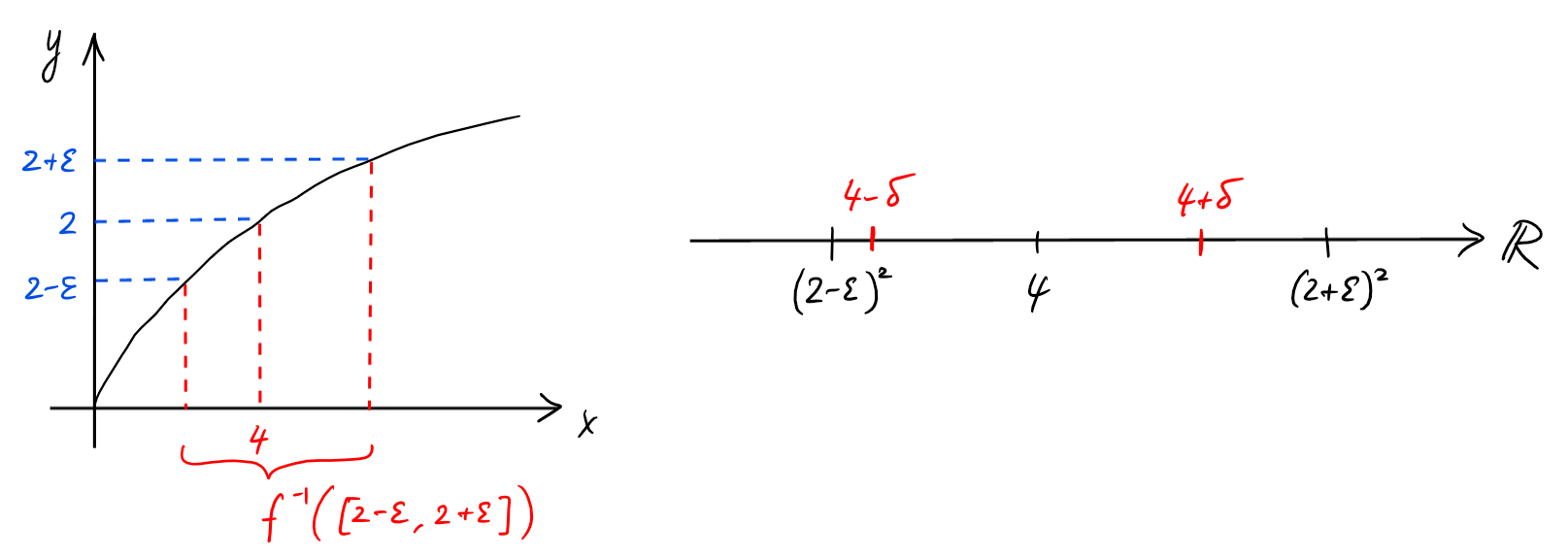3.2 Limites \(x\to x_0\)
Ayant étudié les limites de fonctions lorsque \(x\rightarrow \pm \infty\), on va
maintenant s'intéresser au comportement des fonctions lorsque \(x\) tend vers un
point \(x_0\in \mathbb{R}\). L'idée intuitive est que la limite de \(f\) lorsque
\(x\rightarrow x_0\) est égale à \(L\in \mathbb{R}\) si \(f(x)\) devient arbitrairement
proche de \(L\) lorsque \(x\) est suffisamment proche de \(x_0\).
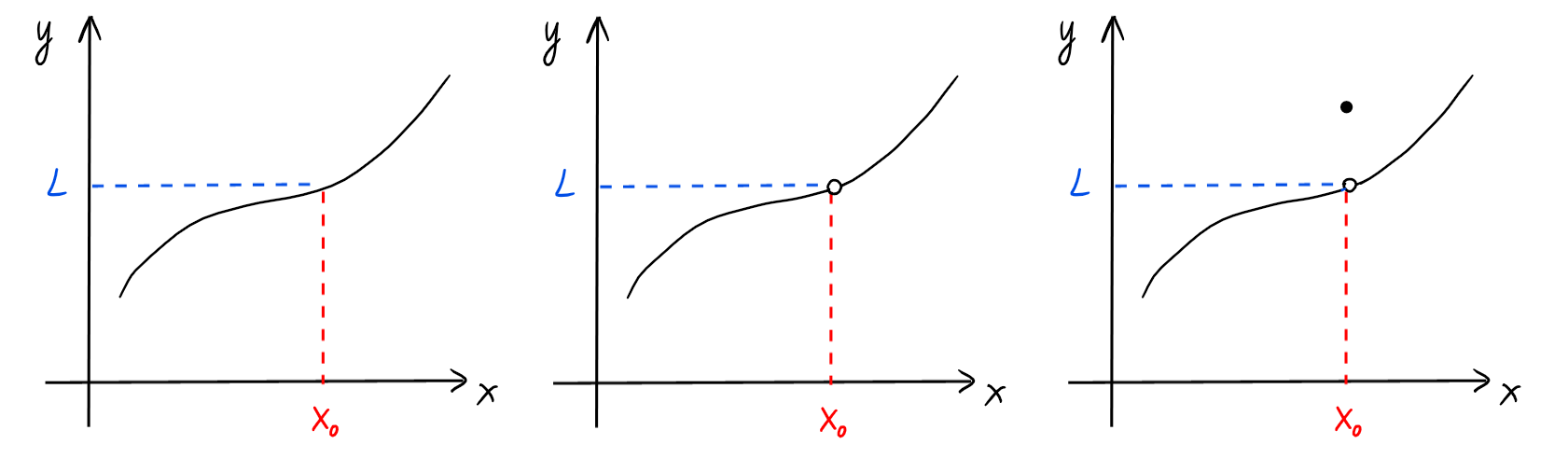
Pour les exemples au-dessus, la valeur de la limite en \(x_0\) est la même ! Ce
qui se passe en \(x=x_0\) ne joue aucun rôle dans la valeur de la limite. Ce qui
compte est le comportement de \(f(x)\) lorsque \(x\) s'approche de \(x_0\) sur
un ''voisinage épointé''.
Un voisinage épointé de \(x_0\) est un voisinage de \(x_0\) privé de
\(x_0\).
Par exemple, pour \(\delta\gt 0\), \(\{x\in \mathbb{R}: 0\lt |x-x_0|\leqslant\delta\}\) est
un voisinage épointé. On a
\[\begin{aligned}
\{x\in \mathbb{R}: 0\lt |x-x_0|\leqslant\delta\}
&=\{x\in \mathbb{R}: |x-x_0|\leqslant\delta\}\setminus \{x_0\}\\
&=[x_0-\delta,x_0[\ \cup\ ]x_0,x_0+\delta]\,.
\end{aligned}\]
Soit \(f\) une fonction définie sur un voisinage épointé de \(x_0\in \mathbb{R}\). On
dit que \(f\) tend vers la limite \(L\) lorsque \(x\) tend vers \(x_0\) si
\[\forall \varepsilon\gt 0, \ \exists \delta\gt 0 \ \text{ tel que } \ 0\lt |x-x_0|\leqslant \delta \ \Longrightarrow \ |f(x)-L|\leqslant \varepsilon.\]
On écrit \(\lim_{x\rightarrow x_0} f(x)=L\).
Pour que \(\lim_{x\rightarrow x_0} f(x)=L\), il faut donc que pour tout
\(\varepsilon\gt 0\), on puisse trouver \(\delta\gt 0\) suffisamment petit tel
que le \(\delta\)-voisinage épointé \(\{x\in \mathbb{R}: 0\lt |x-x_0|\leqslant\delta\}\) est
envoyé par \(f\) dans l'\(\varepsilon\)-voisinage de \(L\).
Exemples:
- Soit \(f\) la fonction
\[f(x)=
\begin{cases}
3x & \text{ si } x\neq 2,\\
1 & \text{ si } x=2.
\end{cases}\]
On a \(\lim_{x\rightarrow 2}f(x)=6.\) En effet, étant donné \(\varepsilon\gt
0\), on a que pour tout \(x\neq 2\),
\[\begin{aligned}|f(x)-6|\leqslant \varepsilon
&\iff |3x-6|\leqslant \varepsilon\\
&\iff 3x\in [6-\varepsilon,6+\varepsilon]\\
&\iff x\in\left[2-\frac{\varepsilon}{3}, 2+\frac{\varepsilon}{3}\,.
\right]
\end{aligned}\]
On peut donc prendre \(\delta=\frac{\varepsilon}{3}\). En effet, si
\(\delta=\frac{\varepsilon}{3}\), on a \(|x-2|\leqslant \delta \Longrightarrow
|3x-6|\leqslant \varepsilon\).
- Soit \(f(x)=\sqrt{x}\).
On a \(\lim_{x\rightarrow 4}f(x)=2.\)
En effet, étant donné \(\varepsilon\gt 0\), on a
\[|f(x)-2|\leqslant \varepsilon \iff |\sqrt{x}-2|\leqslant \varepsilon \iff \sqrt{x}\in [2-\varepsilon,2+\varepsilon] \iff x\in [(2-\varepsilon)^2,(2+\varepsilon)^2].\]
Il nous faut alors \(\delta\gt 0\) tel que \(|x-4|\lt \delta\) garantit que
\(x\in [(2-\varepsilon)^2,(2+\varepsilon)^2]\). Il suffit donc de prendre \(0\lt
\delta\lt 4-(2-\varepsilon)^2\), car la distance entre \(4\) et
\((2-\varepsilon)^2\) est plus petite que celle entre \(4\) et
\((2+\varepsilon)^2\).
- Si \(f(x)=\sqrt{x+2}\), montrons que \(\lim_{x\to 1}f(x)=\sqrt{3}\). En
effet, on peut d'abord remarquer que pour tout \(x\geqslant -2\),
\[\begin{aligned}
|f(x)-\sqrt{3}|
&=|\sqrt{x+2}-\sqrt{3}|\\
&=\left|\frac{(x+2)-3}{\sqrt{x+2}+\sqrt{3}}\right|\\
&=\frac{|x-1|}{\sqrt{x+2}+\sqrt{3}}\\
&\leqslant \frac{|x-1|}{\sqrt{3}}\,.
\end{aligned}\]
Dans la dernière ligne, on a utilisé le fait que \(\sqrt{x+2}\geqslant 0\).
Maintenant,
fixons \(\varepsilon\gt 0\). Par ce qui précède, on
peut garantir \(|f(x)-\sqrt{3}|\leqslant \varepsilon\) en imposant
\[
\frac{|x-1|}{\sqrt{3}}\leqslant \varepsilon\,,
\]
qui est équivalente à \(|x-1|\leqslant \sqrt{3}\varepsilon\).
Ceci montre que si on définit
\(\delta:=\sqrt{3}\varepsilon\), alors
\[\begin{aligned}
0\lt |x-1|\leqslant \delta
\quad&\quad\Rightarrow\quad \frac{|x-1|}{\sqrt{3}}\leqslant \varepsilon\\
&\quad\Rightarrow\quad |f(x)-\sqrt{3}|\leqslant \varepsilon\,.
\end{aligned}\]
(On suppose partout que \(x\geqslant -2\).)
- Si \(f(x)=x^2\), montrons que \(\lim_{x\to 2}f(x)=4\).
Commençons par écrire
\[
|f(x)-4|=|x^2-4|=|(x+2)(x-2)|=|x+2|\cdot |x-2|\,.
\]
Cette égalité suggère que \(|f(x)-4|\) devient petit
lorsque la distance
\(|x-2|\) devient petite. Mais la présence du terme \(|x+2|\), qui dépend de
\(x\), complique un peu l'argument.
Procédons comme suit: commençons par nous restreindre à des \(x\) dans un
intervalle centré en \(x_0=2\), de taille fixée, par exemple
\([1,3]\). Remarquons alors que pour tout \(x\in [1,3]\),
\[ |x+2|\leqslant |x|+2\leqslant 3+2=5\,,
\]
et donc aussi
\[
|f(x)-4|=|x+2|\cdot |x-2|\leqslant 5|x-2|\,.
\]
Maintenant, fixons \(\varepsilon\gt 0\). Par ce qui précède, on
peut garantir \(|f(x)-4|\leqslant \varepsilon\) en imposant que \(x\in [1,3]\)
et que
\[
5|x-2|\leqslant \varepsilon\,,
\]
qui est équivalente à \(|x-2|\leqslant \varepsilon/5\).
Ceci montre que si on définit
\(\delta:=\varepsilon/5\), alors
\[\begin{aligned}
0\lt |x-2|\leqslant \delta
\quad&\quad\Rightarrow \quad5|x-2|\leqslant \varepsilon\\
&\quad\Rightarrow\quad |f(x)-4|\leqslant \varepsilon\,.
\end{aligned}\]
(On suppose partout que \(x\in [1,3]\).)
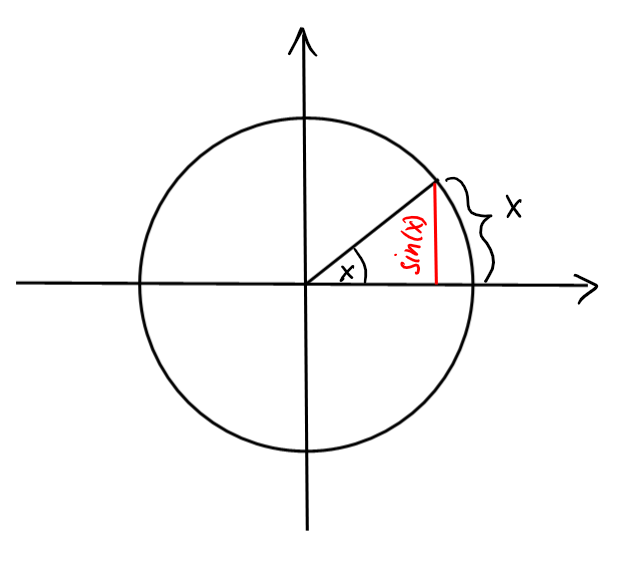
- Soit \(f(x)=\sin(x)\). On a \(\lim_{x\rightarrow 0}f(x)=0.\)
On remarque que \(|\sin(x)|\leqslant |x|\) \(\forall x\). Soit \(\varepsilon\gt 0\). Il nous faut \(\delta\gt 0\) pour que \(|x-0|\leqslant\delta \Longrightarrow |\sin(x)-0|\leqslant \varepsilon\). On voit que \(\delta=\varepsilon\) suffit, et donc on a \(\lim_{x\rightarrow 0}\sin(x)=0.\)
- La limite \(\lim_{x\to 0} \sin\left(\frac{1}{x}\right)\) n'existe pas. On
va voir une façon de montrer ce fait ci-dessous (caractérisation par les
suites).
Encore une fois, toutes les propriétés des limites vues précédemment possèdent
un analogue dans le cas des limites en un point.
En particulier, les limites en un point se comportent bien par rapport aux
sommes, produits, quotients, etc.
Exemples:
- Soit \(f(x)=3x^5\cos(2x)+2x\). On a
\[\begin{aligned}
\lim_{x\rightarrow \frac{\pi}{2}}f(x)
&= \left(
\lim_{x\rightarrow \frac{\pi}{2}}3x^5
\right)
\cdot
\left(\lim_{x\rightarrow \frac{\pi}{2}}\cos(2x)\right)
+\lim_{x\rightarrow \frac{\pi}{2}}2x\\
&=3\left(\frac{\pi}{2}\right)^5\cos(\pi)+2\frac{\pi}{2}\\
&=-3\left(\frac{\pi}{2}\right)^5+\pi\,.
\end{aligned}\]
- Soit \(f(x)=x\sin\left(\frac{1}{x}\right)\). On a \(\lim_{x\rightarrow
0}f(x)=0\) car \(\lim_{x\rightarrow 0}x=0\) et la fonction
\(\sin\left(\frac{1}{x}\right)\) est bornée.
- Dans l'exemple suivant, on enlève l'indétermination en sortant un facteur ''caché'':
\[
\lim_{x\rightarrow 1}\frac{x^2-3x+2}{x^2+2x-3}
=\lim_{x\rightarrow 1}\frac{(x-1)(x-2)}{(x-1)(x+3)}
=\lim_{x\rightarrow 1}\frac{x-2}{x+3}=\frac{-1}{4}\,.
\]
- Soit \(f(x)=\frac{\sqrt{x+3}-(x+1)}{x-1}\). Calculons
\(\lim_{x\rightarrow 1}f(x)\).
Puisque \(x-1, \sqrt{x+3}-(x+1)\rightarrow 0\) lorsque \(x\rightarrow 1\), on a
une indétermination du type ''\(\frac{0}{0}\)''. On a
\[\begin{aligned}
\frac{\sqrt{x+3}-(x+1)}{x-1}&=\frac{\sqrt{x+3}-(x+1)}{x-1}\cdot
\frac{\sqrt{x+3}+(x+1)}{\sqrt{x+3}+(x+1)}\\
&= \frac{x+3-(x+1)^2}{(x-1)\left(\sqrt{x+3}+(x+1)\right)}\\
&= \frac{-x^2-x+2}{(x-1)\left(\sqrt{x+3}+(x+1)\right)}\\
&= \frac{-(x-1)(x+2)}{(x-1)\left(\sqrt{x+3}+(x+1)\right)}\\
&= \frac{-(x+2)}{\sqrt{x+3}+(x+1)},
\end{aligned}\]
où la dernière égalité est valide car on étudie cette fonction sur un voisinage
épointé de \(1\), et donc \(x\neq 1\).
On a donc
\[
\lim_{x\rightarrow 1}f(x)
= \lim_{x\rightarrow 1}\frac{-(x+2)}{\sqrt{x+3}+(x+1)}=\frac{3}{4}\,.
\]
Remarque: ce qui nous a permis de calculer la limite était de faire apparaître
un facteur \((x-1)\) ''caché'' au numérateur et au dénominateur.
- Si \(f(x) = \frac{x^3+px-3}{x^2-4x+3}\), pour quelle(s) valeur(s) du
paramètre \(p\) est-ce que \(f\) admet une limite finie
en \(x_0 = 1\)? Et lorsque cette limite existe, que vaut-elle?
On remarque que la limite du dénominateur est
\[\lim_{x\rightarrow 1} (x^2-4x+3) = 0\,.
\]
Donc, pour que \(f\) admette une limite en \(1\), il est
nécessaire que la limite du numérateur soit également nulle. Comme
cette dernière est égale à
\[
\lim_{x\rightarrow 1} (x^3+px-3) = p - 2\,,
\]
il faut donc que \(p = 2\). Pour cette valeur de \(p\),
le numérateur devient le polynôme
\[ P(x)=x^3+2x-3\,,
\]
qui possède \(x_0=1\) comme racine. Or ceci implique (voir cours d'Analyse A)
que \(P\) peut se factoriser:
\[ P(x)=(x-1)(x^2+x+3)\,.
\]
Ainsi, la fonction devient
\[
f(x)
=\frac{P(x)}{x^2-4x+3}
=\frac{(x-1)(x^2+x+3)}{(x-1)(x-3)}
=\frac{x^2+x+3}{x-3}\,,
\]
et donc
\[
\lim_{x\rightarrow 1} f(x)
=\lim_{x\rightarrow 1} \frac{x^2+x+3}{x-3}
=-\frac{5}{2}\,.
\]
On a aussi une version du Théorème des deux gendarmes pour les limites en un point.
Théorème:[Théorème des deux gendarmes, \(x\rightarrow x_0\)]
Soient \(f, g\) et \(h\) des fonctions définies sur un voisinage épointé de \(x_0\in\mathbb{R}\) telles que
- \(g(x)\leqslant f(x) \leqslant h(x)\) sur un voisinage épointé de \(x_0\), et
- \(\lim_{x\rightarrow x_0} g(x)=\lim_{x\rightarrow x_0} h(x)=L\),
alors \(\lim_{x\rightarrow x_0} f(x)=L\).
Exemple:
Soit \(f(x)=(x^2-1)\cos\left(\frac{1}{x-1}\right)\) \((x\neq 1)\). On a \(\lim_{x\rightarrow 1} f(x)=0\). En effet,
\[-(x^2-1)\leqslant f(x)\leqslant x^2-1,\]
puisque \(-1\leqslant \cos\left(\frac{1}{x-1}\right)\leqslant 1\), et \(\lim_{x\rightarrow 1} -(x^2-1)=\lim_{x\rightarrow 1} (x^2-1)=0\). Donc par le théorème des deux gendarmes, on a \(\lim_{x\rightarrow 1} f(x)=0\).
On a également une caractérisation par les suites dans le cas de \(x\rightarrow x_0\).
Théorème:[Caractérisation par les suites]
Soit \(f\) définie sur un voisinage épointé de \(x_0\in\mathbb{R}\).
\(\lim_{x\rightarrow x_0} f(x)=L \iff\) pour toute suite
\(x_n\neq x_0\)
telle que \(x_n\rightarrow x_0\), on a \(\lim_{n\rightarrow \infty} f(x_n)=L\).
Ce théorème sert principalement à montrer qu'une limite n'existe pas.
Exemple:
- La limite \(\lim_{x\to 0} \sin\left(\frac{1}{x}\right)\) n'existe pas. En effet, en prenant la suite \(x_n:=\frac{1}{\pi/2 + n\pi}\), on a \(x_n\to 0\), mais
\(\lim_{n\to \infty} f(x_n)=\lim_{n\to \infty} \sin\left(\frac{1}{x_n}\right)=\lim_{n\to \infty} \sin(\pi/2 + n\pi)=\lim_{n\to \infty} (-1)^n\) n'existe pas.
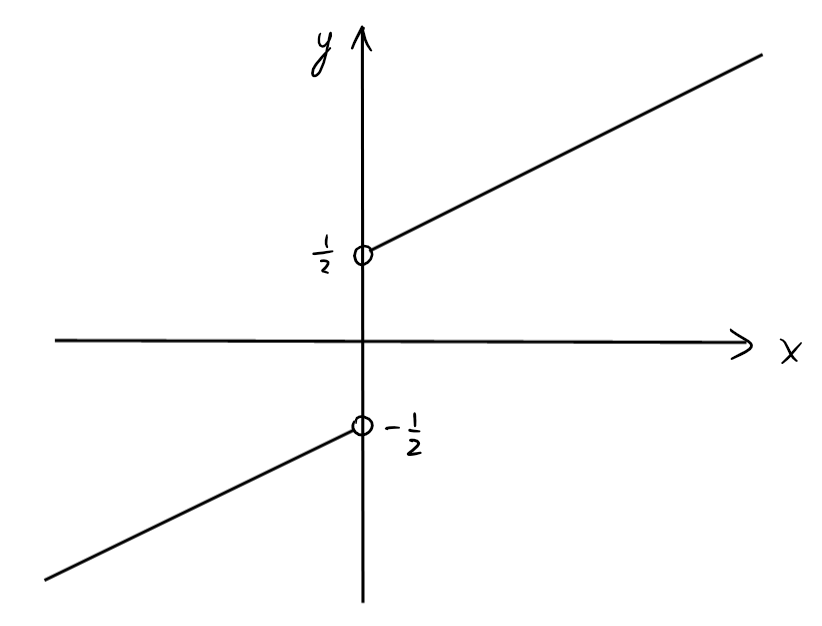
- Soit \(f(x)=\frac{x}{2}+\frac{x}{2|x|}\). Cette fonction est définie sur \(\mathbb{R}\setminus\{0\}\). On a
\[f(x)=
\begin{cases}
\frac{x}{2}+\frac{x}{2x}=\frac{x}{2}+\frac{1}{2} & \text{ si } x\gt 0,\\ \\
\frac{x}{2}+\frac{x}{2(-x)}=\frac{x}{2}-\frac{1}{2} & \text{ si } x\lt 0.
\end{cases}\]
On montre que \(\lim_{x\rightarrow 0} f(x)\) n'existe pas. En effet,
pour \(a_n:=\frac{1}{n}\), \(\lim_{n\rightarrow \infty} f(a_n)=\lim_{n\rightarrow \infty} \frac{1}{2n}+\frac{1}{2}=\frac{1}{2}\), et
pour \(b_n:=\frac{-1}{n}\), \(\lim_{n\rightarrow \infty} f(b_n)=\lim_{n\rightarrow \infty} \frac{-1}{2n}-\frac{1}{2}=-\frac{1}{2}\).
Pourtant, \(\lim_{n\rightarrow \infty}a_n=\lim_{n\rightarrow \infty}b_n=0\). La limite \(\lim_{x\rightarrow 0} f(x)\) n'existe donc pas par la caractérisation par les suites.
Remarque:
- Pour montrer que \(\lim_{x \to x_0} f(x) \neq L\), il suffit de trouver
une suite \(x_n\to x_0\) telle que \(\lim_{n\to \infty} f(x_n) \neq L\).
- Pour montrer que \(\lim_{x \to x_0} f(x)\) n'existe pas, il suffit de
trouver une suite \(x_n\to x_0\) telle que \(\lim_{n\to \infty} f(x_n)\)
n'existe pas. On peut aussi exhiber deux suites \((a_n)\) et \((b_n)\) telles
que \(\lim_{n\to \infty} a_n=x_0=\lim_{n\to \infty} b_n\), mais \(\lim_{n\to
\infty} f(a_n)\neq \lim_{n\to \infty} f(b_n)\).