3.4 Infiniment petits équivalents (IPE)
Les infiniment petits équivalents nous permettront de calculer les limites en
comparant des fonctions qui tendent vers zéro ''à la même vitesse''.
Soient \(f\) et \(g\) définies sur un voisinage épointé de \(x_0\in\mathbb{R}\), telles
que \(g(x)\neq 0\) sur un voisinage épointé de \(x_0\). Les fonctions \(f\) et
\(g\) sont des
infiniment petits équivalents (IPE) au voisinage de
\(x_0\) si
- \(\lim_{x\rightarrow x_0} f(x)= \lim_{x\rightarrow x_0} g(x)=0\)
(infiniment petits), et
- \(\lim_{x\rightarrow x_0} \frac{f(x)}{g(x)}=1\) (équivalents).
On écrit \(f\sim g\) au voisinage de \(x_0\).
Remarque:
On peut définir de manière équivalente les IPE dans un voisinage à gauche ou à droite
d'un point \(x_0\), ou dans un voisinage de l'infini.
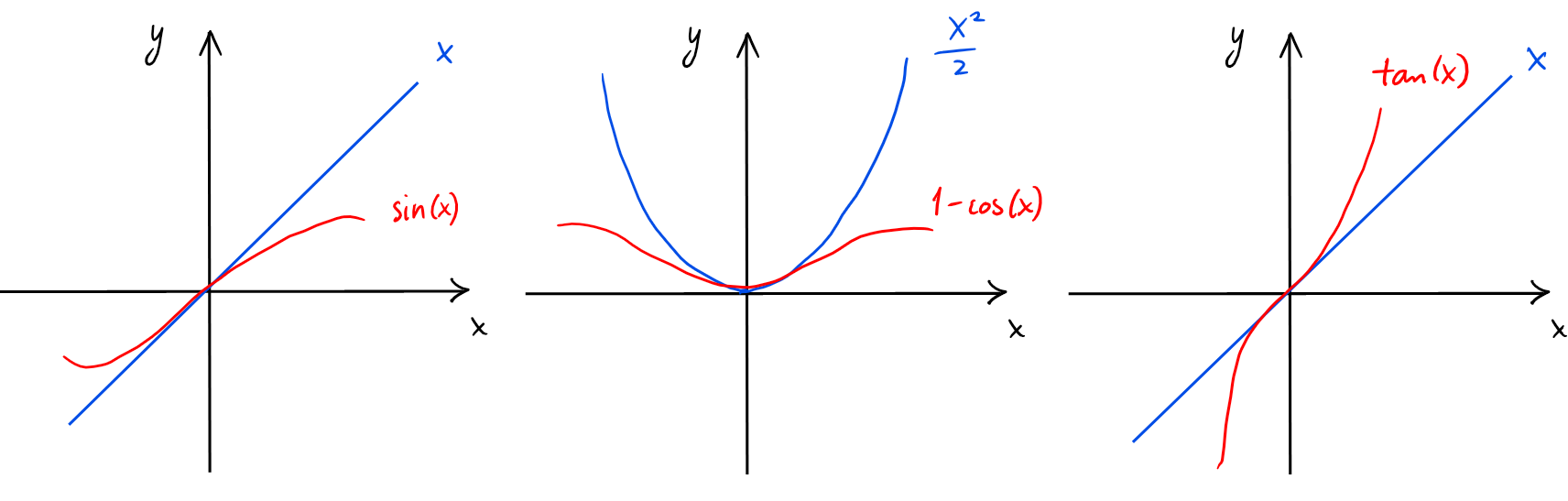
Au voisinage de \(x_0=0\),
- \(\sin(x)\sim x\),
- \(\tan(x)\sim x\),
- \(1-\cos(x) \sim \frac{x^2}{2}\).
Preuve:
On l'a déjà dit, \(\lim_{x\rightarrow 0} \sin(x)= \lim_{x\rightarrow 0} x=0\).
Pour montrer que \(\lim_{x\rightarrow 0} \frac{\sin(x)}{x}=1\), il suffit de
montrer que \(\lim_{x\rightarrow 0^+} \frac{\sin(x)}{x}=1\), puisque la fonction
\(\frac{\sin(x)}{x}\) est paire. Soit \(0\lt x\lt \frac{\pi}{2}\). On compare
des aires dans le dessin suivant d'un quart de cercle trigonométrique.
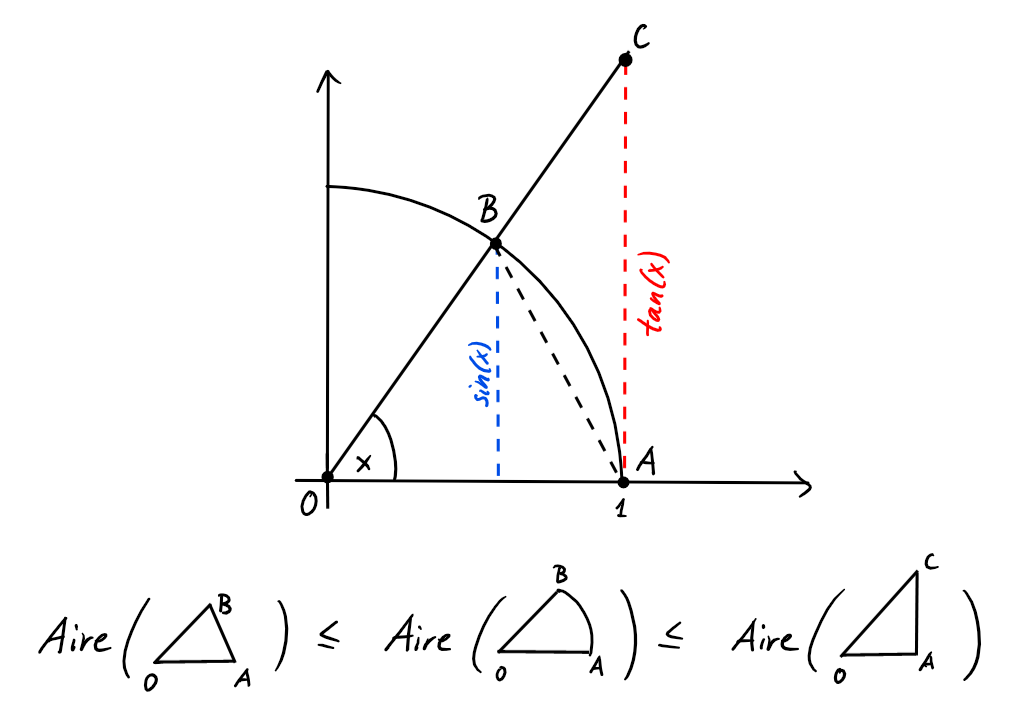
On a donc
\[\begin{aligned}
\frac{1}{2}\cdot 1 \cdot &\sin(x) \ \leqslant \ \pi\cdot 1^2\cdot \frac{x}{2\pi} \ \leqslant \ \frac{1}{2}\cdot 1 \cdot \tan(x)\\
&\iff \frac{\sin(x)}{2} \leqslant \frac{x}{2} \leqslant \frac{\tan(x)}{2}\\
&\iff \sin(x)\leqslant x\leqslant \tan(x)\\
&\iff 1\leqslant \frac{x}{\sin(x)} \leqslant \frac{1}{\cos(x)}\\
&\iff \cos(x)\leqslant \frac{\sin(x)}{x} \leqslant 1\,.
\end{aligned}\]
(Ces manipulations sont justifiées par le fait que
\(\sin(x),\cos(x),x \gt 0\)). Puisque \(\lim_{x\rightarrow 0}\cos(x)=1\), le
Théorème des deux gendarmes implique que
\(\lim_{x\rightarrow 0}\frac{\sin(x)}{x}=1\).
Ceci montre que \(\sin(x)\sim x\) au voisinage de \(0\).
On a \(\lim_{x\rightarrow 0} \tan(x)= \lim_{x\rightarrow 0} x=0\), et
\[
\lim_{x\rightarrow 0}
\frac{\tan(x)}{x}
=\lim_{x\rightarrow 0}
\frac{\sin(x)}{x}\cdot \frac{1}{\cos(x)}
=1
\]
puisque \(\lim_{x\rightarrow 0}\frac{\sin(x)}{x}=1\) par le raisonnement au-dessus, et \(\lim_{x\rightarrow 0}\frac{1}{\cos(x)}=1.\)
Remarquons pour commencer que
\(\lim_{x\rightarrow 0} (1-\cos(x))= 0\), et
\(\lim_{x\rightarrow 0} \frac{x^2}{2}=0\). Ensuite,
on peut écrire
\[\begin{aligned}
\frac{1-\cos(x)}{x^2/2}
&=
\frac{1-\cos(x)}{x^2/2}\cdot \frac{1+\cos(x)}{1+\cos(x)}\\
&=
\frac{1-\cos^2(x)}{x^2}\cdot
\frac{2}{1+\cos(x)}\\
&=
\left(\frac{\sin(x)}{x}\right)^2\cdot
\frac{2}{1+\cos(x)}\,,
\end{aligned}\]
et donc
\[\begin{aligned}
\lim_{x\rightarrow 0}
\frac{1-\cos(x)}{x^2/2}
&=
\left(
\lim_{x\rightarrow 0}
\frac{\sin(x)}{x}
\right)^2
\cdot
\left(
\lim_{x\rightarrow 0}
\frac{2}{1+\cos(x)}
\right)\\
&=1^2\cdot 1=1\,.
\end{aligned}\]
Dans un calcul de limite, on peut remplacer une fonction par son IPE dans une
expression factorisée.
En effet, si \(f\sim \widetilde{f}\) au voisinage de \(x_0\),
\[\begin{aligned}
\lim_{x\rightarrow x_0} \left[f(x)\cdot h(x)\right]&=\lim_{x\rightarrow x_0}
\left[\frac{f(x)}{\widetilde{f}(x)}\cdot \widetilde{f}(x)\cdot h(x)\right]\\
&=\lim_{x\rightarrow x_0} \frac{f(x)}{\widetilde{f}(x)}\cdot \lim_{x\rightarrow x_0} \left[\widetilde{f}(x)\cdot h(x)\right]\\
&=\lim_{x\rightarrow x_0} \left[\widetilde{f}(x)\cdot h(x)\right]\,.
\end{aligned}\]
Et dans un quotient, si \(f\sim \widetilde{f}\) et
\(g\sim \widetilde{g}\) au voisinage de \(x_0\), alors
\[
\lim_{x\to x_0}
\frac{f(x)}{g(x)}
=
\lim_{x\to x_0}
\frac{f(x)}{\widetilde{f}(x)}
\frac{\widetilde{f}(x)}{\widetilde{g}(x)}
\frac{\widetilde{g}(x)}{g(x)}
=
\lim_{x\to x_0}
\frac{\widetilde{f}(x)}{\widetilde{g}(x)}
\]
Exemple:
Considérons
\[
\lim_{x\rightarrow 0} \frac{\sin^2(x)}{4-4\cos(x)}\,.
\]
Puisque \(\sin(x)\sim x\) et \(1-\cos(x)\sim x^2/2\) au voisinage de \(x_0=0\),
\[
\lim_{x\rightarrow 0} \frac{\sin^2(x)}{4-4\cos(x)}
=\lim_{x\rightarrow 0}\frac{\sin(x)\cdot\sin(x)}{4(1-\cos(x))}
=\lim_{x\rightarrow 0} \frac{x\cdot x}{4(x^2/2)}
=\frac{1}{2}\,.
\]
On peut faire des changements de variable pour se ramener aux IPE connus.
Exemple:
Considérons
\[
\lim_{x\rightarrow -\pi/2} \ \frac{x+\frac{\pi}{2}}{\cos(x)}\,.
\]
Si on pose \(y=x+\frac{\pi}{2}\),
\[\begin{aligned}
\lim_{x\rightarrow -\pi/2} \ \frac{x+\frac{\pi}{2}}{\cos(x)}
&=
\lim_{y\rightarrow 0} \frac{y}{\cos\left(y-\frac{\pi}{2}\right)}\\
&=\lim_{y\rightarrow 0} \frac{y}{\sin\left(y\right)}\\
&=1.
\end{aligned}\]
Notons aussi que, par exemple, on a \(\sin(5x^3)\sim 5x^3\) au voisinage de
\(0\), puisque \(\lim_{x\rightarrow 0} 5x^3=0\).
Attention: on ne peut pas remplacer une fonction par son IPE dans un calcul de
limite d'une somme, comme montre l'exemple suivant.
Exemple:
Considérons
\[
\lim_{x\rightarrow 0}
\frac{\sin(2x)-2\sin(x)}{x^3}\,.
\]
Une façon correcte de calculer cette limite, est de commencer par factoriser:
\[\begin{aligned}
\lim_{x\rightarrow 0} \frac{\sin(2x)-2\sin(x)}{x^3}
&=\lim_{x\rightarrow 0} \frac{2\sin(x)\cos(x)-2\sin(x)}{x^3}\\
&=\lim_{x\rightarrow 0} \frac{-2\sin(x)(1-\cos(x))}{x^3}\\
&=\lim_{x\rightarrow 0} \frac{-2x(x^2/2)}{x^3}=-1.
\end{aligned}\]
On remarque que si on avait voulu utiliser dès le début le fait que
\(\sin (x)\sim x\) et
\(\sin(2x)\sim 2x\) au voisinage de \(x_0=0\), en remplaçant par les équivalents
on aurait trouvé un résultat faux:
\[
\lim_{x\rightarrow 0} \frac{2x-2x}{x^3}
=\lim_{x\rightarrow 0} \frac{0}{x^3}
=0\,.
\]


