7.11 Volumes de solides

Dans cette section, on utilise le calcul intégral pour calculer le volume de certains solides tridimensionnels.

Puisqu'on ne traite dans ce cours que de l'analyse d'une variable réelle, ces solides devront être d'un type particulier.

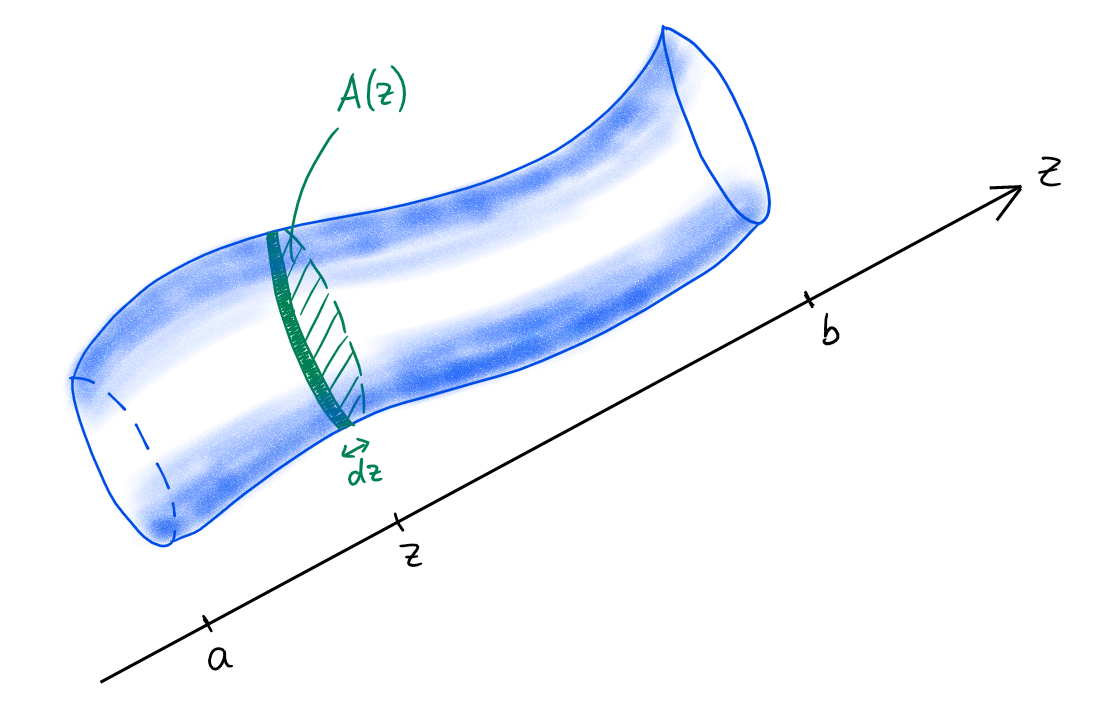
Plus précisément, on supposera qu'il existe toujours un axe selon lequel on peut utiliser une variable, disons \(z\), de façon à ce que la section du solide qui est perpendiculaire à l'axe en \(z\) soit d'aire connue \(A(z)\):

Une tranche infinitésimale d'aire \(A(z)\) et d'épaisseur \(dz\) a un volume infinitésimal donné par \[ dV(z)=A(z)\,dz\,. \] Ainsi, le volume du solide s'obtient en intégrant les tranches: \[ V =\int_a^b dV(z) =\int_a^b A(z)\, dz \]

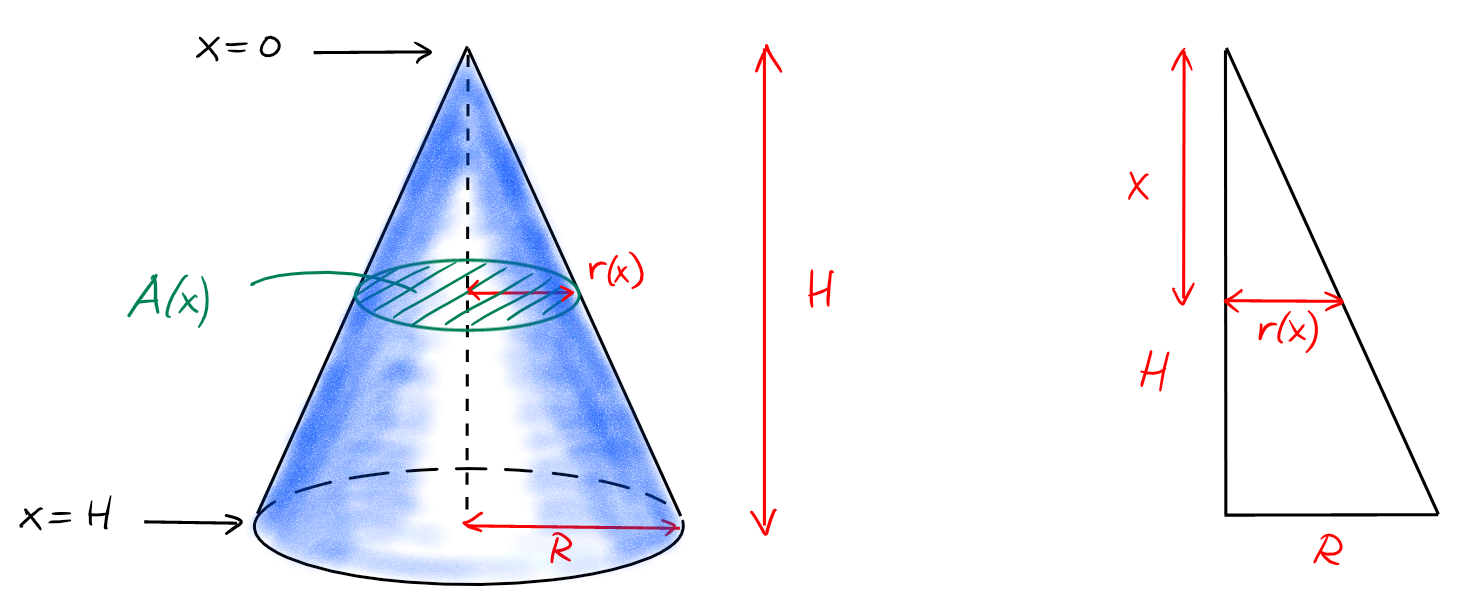
Exemple: Calculons le volume \(V\) d'un cône de hauteur \(H\), dont la base est un disque de rayon \(R\).

Ici, l'axe naturel est celui qui dirige l'axe du cône. Une section perpendiculaire à cet axe est aussi un disque. Si on paramétrise la hauteur des sections par la variable \(x\) qui mesure la distance au sommet (donc \(0\leqslant x\leqslant H\), alors l'aire de la section à hauteur \(x\) est donnée par \(A(x)=\pi r(x)^2\), où \(r(x)\) est le rayon du disque à la hauteur \(x\), et le volume infinitésimal de la tranche correspondante par \(dV(x)=A(x)\,dx=\pi r(x)^2\,dx\). Puisque \(r(x)=\frac{R}{H} x\), \[\begin{aligned} V =\int_0^H dV(x) &=\int_0^H \pi r(x)^2\ dx\\ &=\pi\left(\frac{R}{H} \right)^2\int_0^H x^2 \ dx\\ &=\pi\left(\frac{R}{H} \right)^2\cdot \frac{H^3}{3}\\ &=\frac{1}{3}\cdot\underbrace{(\pi R^2)}_{\text{aire de la base}}\cdot H \end{aligned}\]

Ce raisonnement peut être adapté pour montrer que le volume \(V\) d'un cône de base quelconque est donné par \[V=\frac{1}{3}\cdot A \cdot H\,,\] où \(A\) est l'aire de la base.

Solides de révolution

Une classe de solides que l'on peut traiter à l'aide de calcul intégral d'une seule variable est celle des solides de révolution, obtenus par la rotation d'une région autour d'un axe.

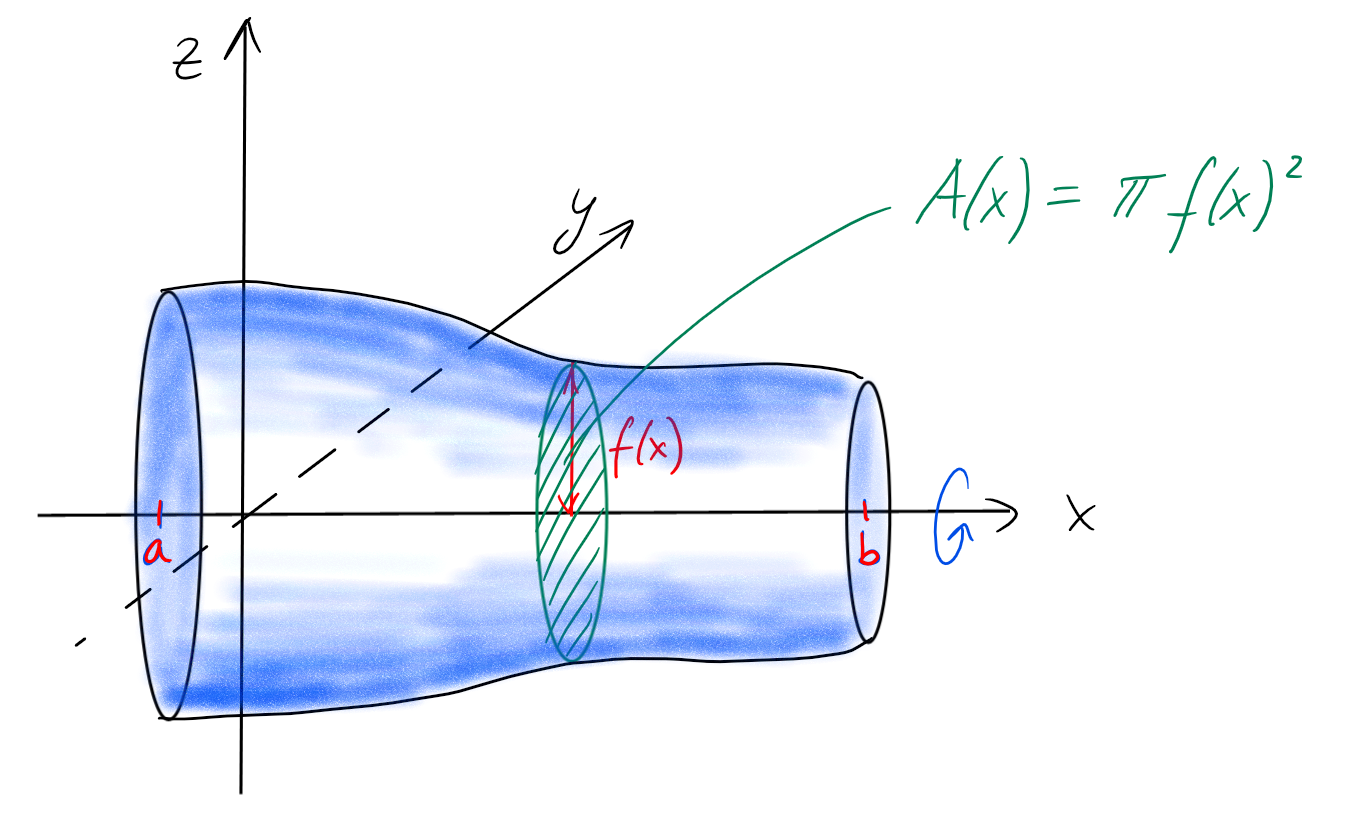
Par exemple, on peut considérer la rotation de la région située sous le graphe d'une fonction \(f:[a,b]\to \mathbb{R}\) continue, autour de \(Ox\). Dans ce cas, les sections du solide de révolution obtenu sont des disques, et le disque en \(x\) a un rayon égal à \(f(x)\):

Le volume est donc \[\begin{aligned} V &=\int_a^b dV(x)\\ &=\int_a^b A(x) \ dx =\int_a^b \pi \cdot f(x)^2 \ dx. \end{aligned}\] Lorsque la rotation du graphe se fait autour d'un autre axe, il faut adapter cette construction.

Exemples: Soit \(f(x)=\sqrt{x-1}\), \(x\in [1,2]\).

On considère la rotation du graphe de \(f\) autour de plusieurs axes.

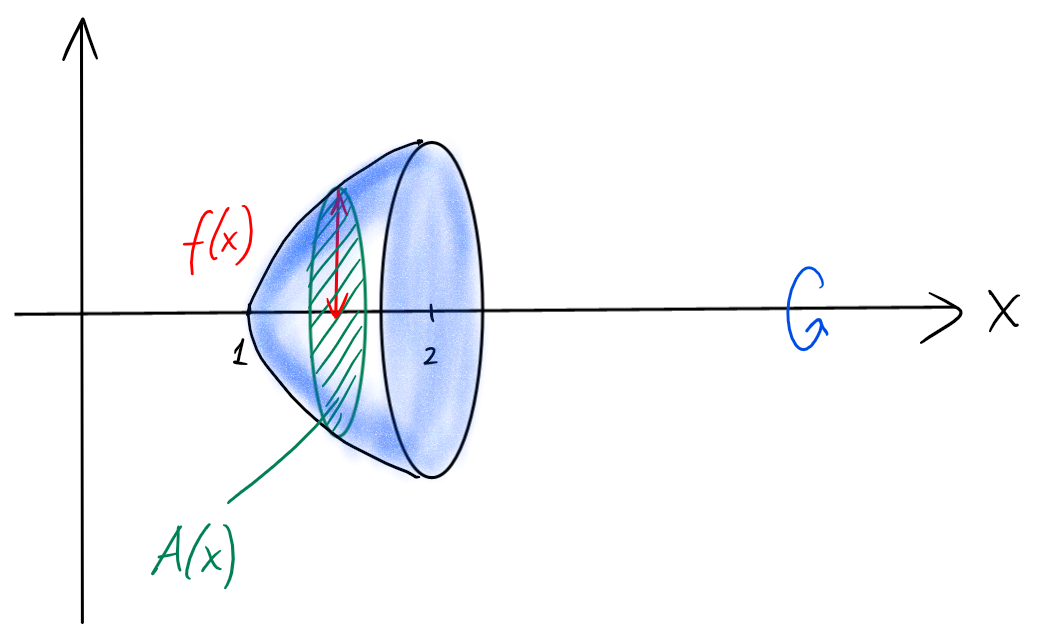
• Rotation autour de \(Ox\):
  
  Dans ce cas, comme on a dit ci-dessus, les sections sont des disques de rayon \(f(x)\), et donc \[ V = \int_1^2 \pi\cdot f(x)^2 \ dx = \pi \int_1^2 (x-1) \ dx =\frac{\pi}{2}. \]
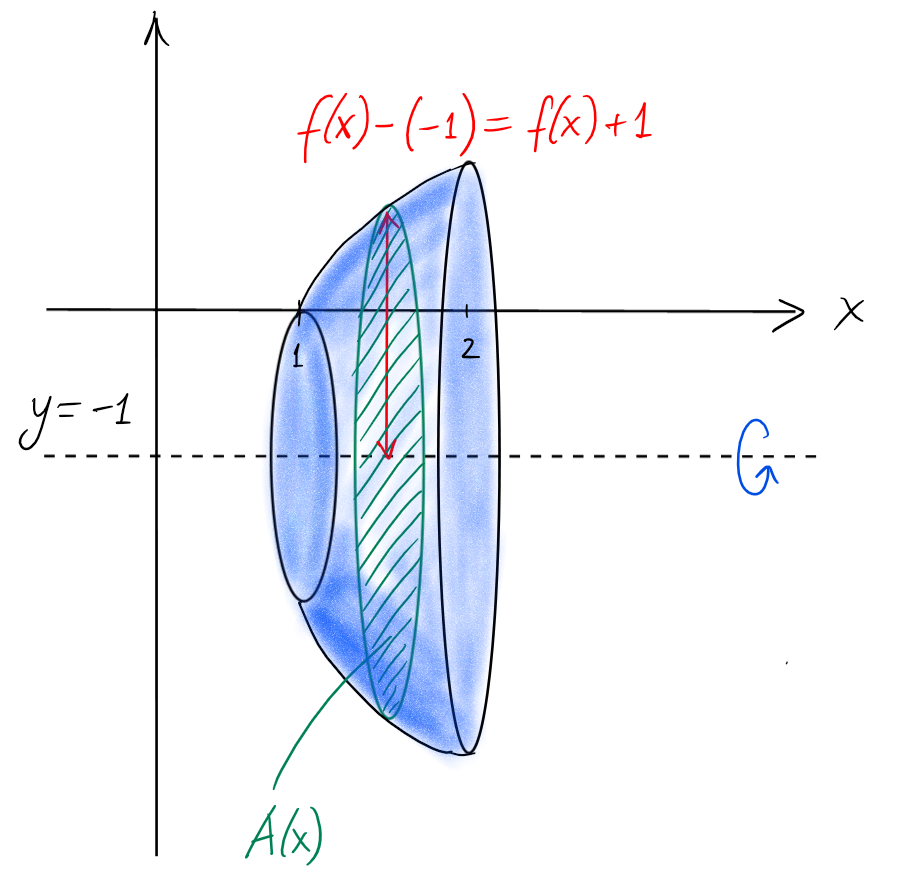
• Rotation autour de la droite horizontale \(y=-1\):
  
  Dans ce cas, la section est un disque de rayon égal à \(f(x)-(-1)=f(x)+1\), et donc \[\begin{aligned} V=\int_1^2 dV(x) &= \int_1^2 \pi\cdot\left(\sqrt{x-1}-(-1)\right)^2 \ dx\\ &= \pi\cdot \int_1^2 (x+2\sqrt{x-1}) \ dx\\ &=\frac{17\pi}{6}. \end{aligned}\]
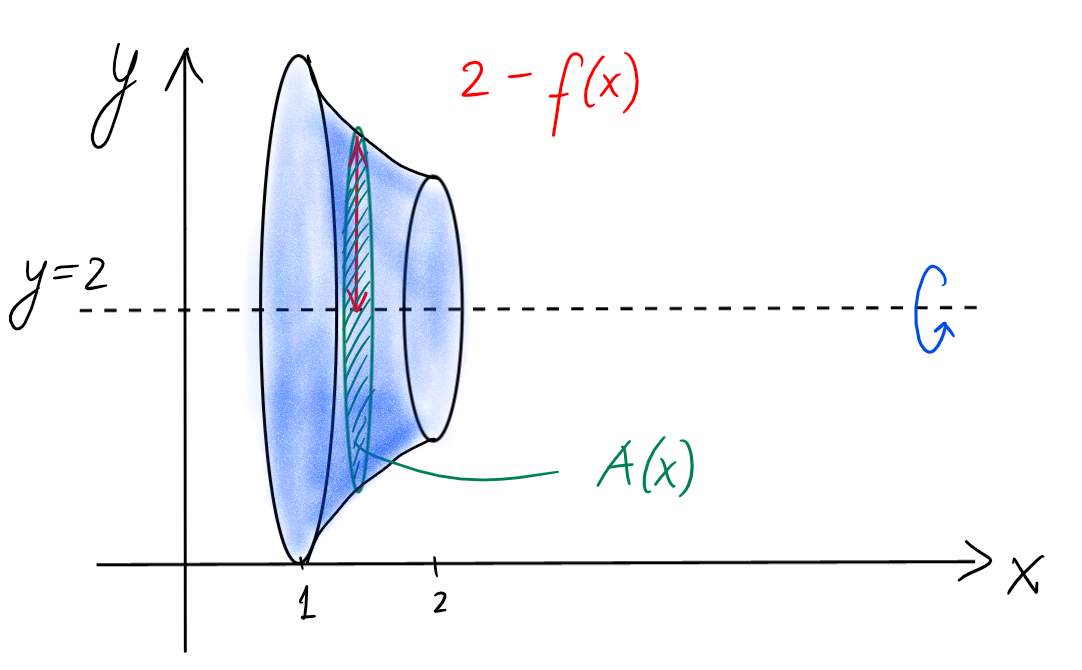
• Rotation autour de la droite horizontale \(y=2\):
  
  Dans ce cas, la section est un disque de rayon égal à \(2-f(x)\), d'aire \(A(x)=\pi(2-f(x))^2\), et donc \[\begin{aligned} V=\int_1^2 dV(x) &= \int_1^2 \pi\cdot\left(2-\sqrt{x-1}\right)^2 \ dx\\ &=\pi\cdot\int_1^2 (3+x-4\sqrt{x-1}) \ dx\\ &=\frac{11\pi}{6}. \end{aligned}\]
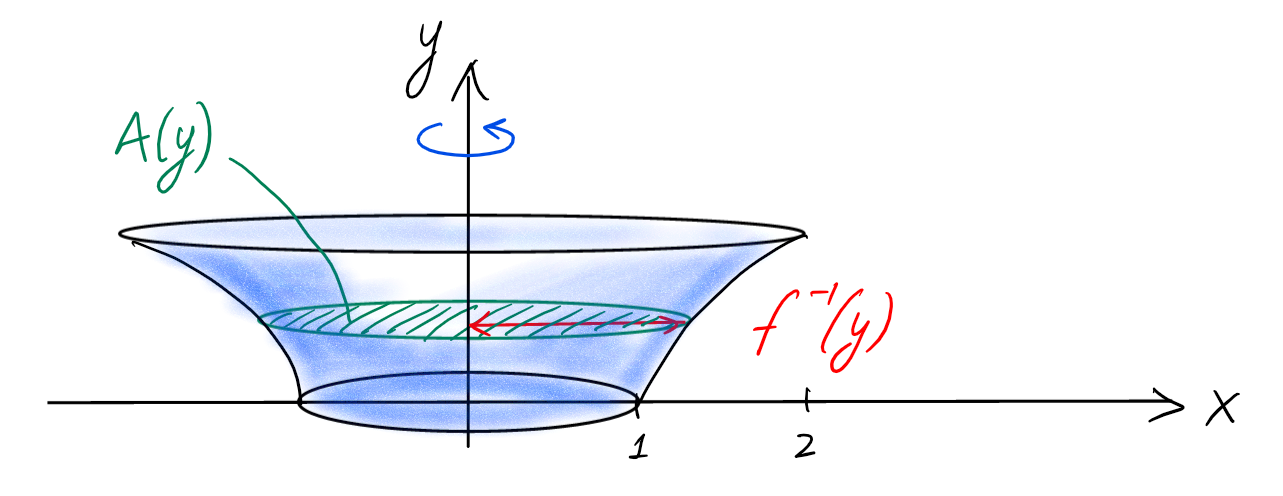
• Rotation autour de l'axe vertical \(Oy\):
  
  Dans ce cas, la variable naturelle est \(y\in [0,1]\), et la section à hauteur \(y\) est un disque de rayon \(f^{-1}(y)\). Or \[ y=f(x)=\sqrt{x-1} \iff x=f^{-1}(y)=y^2+1\,, \] et donc ce disque a une aire \(A(y)=\pi(y^2+1)^2\): \[\begin{aligned} V=\int_0^1 dV(y) &= \int_0^1 \pi\cdot(y^2+1)^2 \ dy\\ &=\frac{28\pi}{15}. \end{aligned}\]
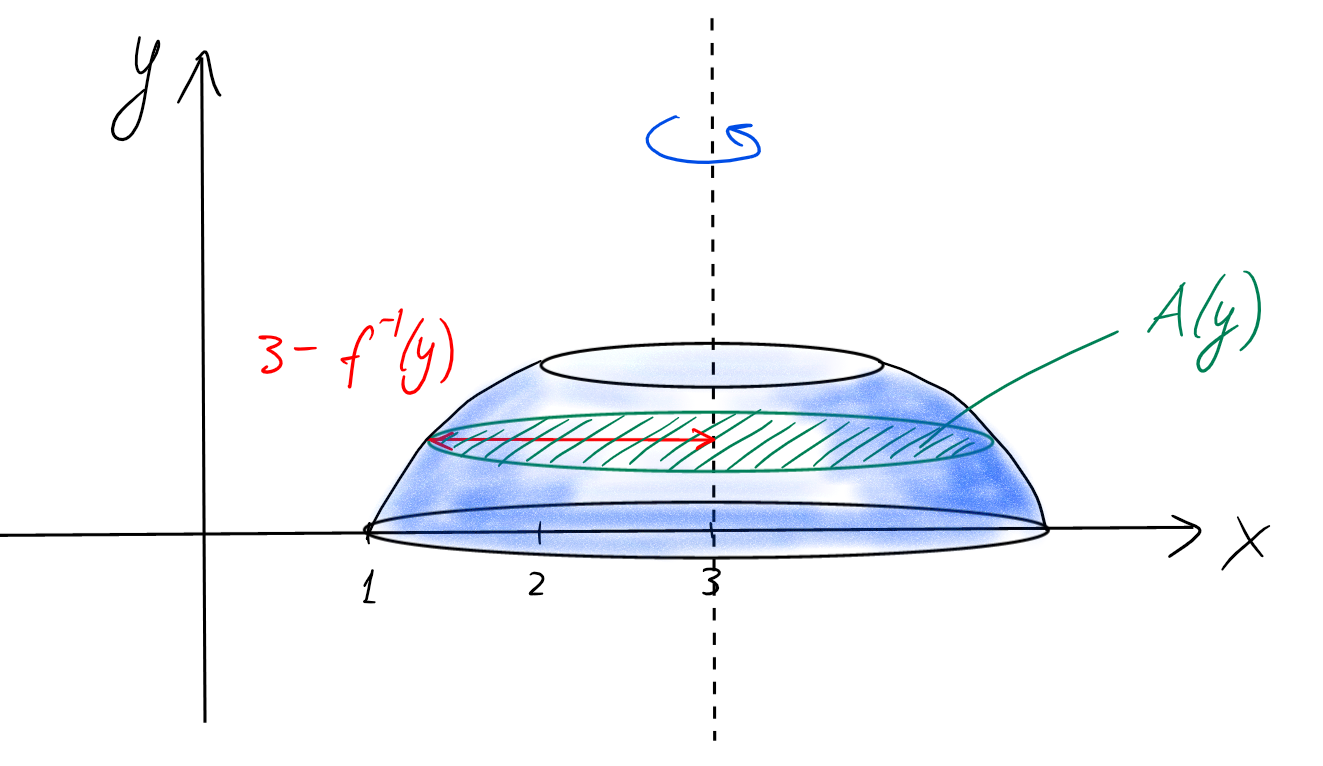
• Rotation autour de la droite verticale \(x=3\):
  
  Dans ce cas, la section est un disque de rayon \(3-f^{-1}(y)\), et donc d'aire \(A(y)=\pi(3-(y^2+1))^2\) \[\begin{aligned} V=\int_0^1 dV(y) \ dy &= \pi \cdot \int_0^1 (4-4y^2+y^4) \ dy\\ &=\frac{43\pi}{15}. \end{aligned}\]

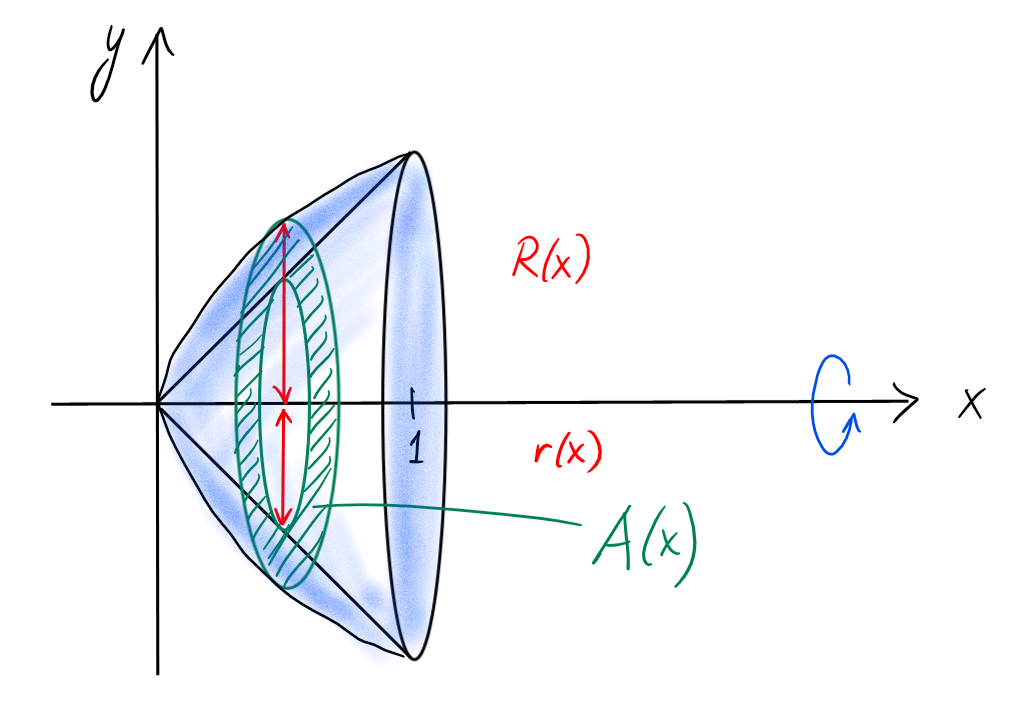
Exemple: Soit \(R\) la région du plan délimitée par les courbes \[y=x \quad \text{ et } \quad x=y^2.\] Calculons le volume du solide obtenu par la rotation de \(R\) autour de l'axe \(Ox\).

Remarquons que la courbe \(x=y^2\) intersecte la droite \(y=x\) aux points \(x=0\) et \(x=1\).

Aussi, la section obtenue en fixant \(x\in [0,1]\) est un anneau,

• de rayon extérieur \(R(x)=\sqrt{x}\) (la réciproque de \(x=g(y)=y^2\)), et
• de rayon intérieur \(r(x)=x\).

Donc son aire se calcule comme une différence de deux disques: \[ A(x)=\pi \cdot R(x)^2-\pi\cdot r(x)^2\,. \] Ainsi, \[\begin{aligned} V&= \int_0^1 A(x) \ dx\\ &= \int_0^1 [\pi\cdot \sqrt{x}^2-\pi\cdot x^2] \ dx = \frac{\pi}{6}. \end{aligned}\] On remarque que ce volume peut aussi être calculé par \(V=V_1-V_2\), où

• \(V_1\) est le volume du solide extérieur (obtenu par la rotation de \(\sqrt{x}\) autour de \(Ox\)),
• \(V_2\) est le volume du solide intérieur (obtenu par la rotation de \(x\) autour de \(Ox\)).

Rotation d'un arc paramétré

Soit maintenant \[\begin{aligned} M:[\alpha,\beta]&\to \mathbb{R}^2\\ t&\mapsto M(t)=(x(t),y(t)) \end{aligned}\] une courbe paramétrée, comme dans la section précédente.

Considérons la rotation de la courbe autour d'un axe, par exemple \(Ox\):

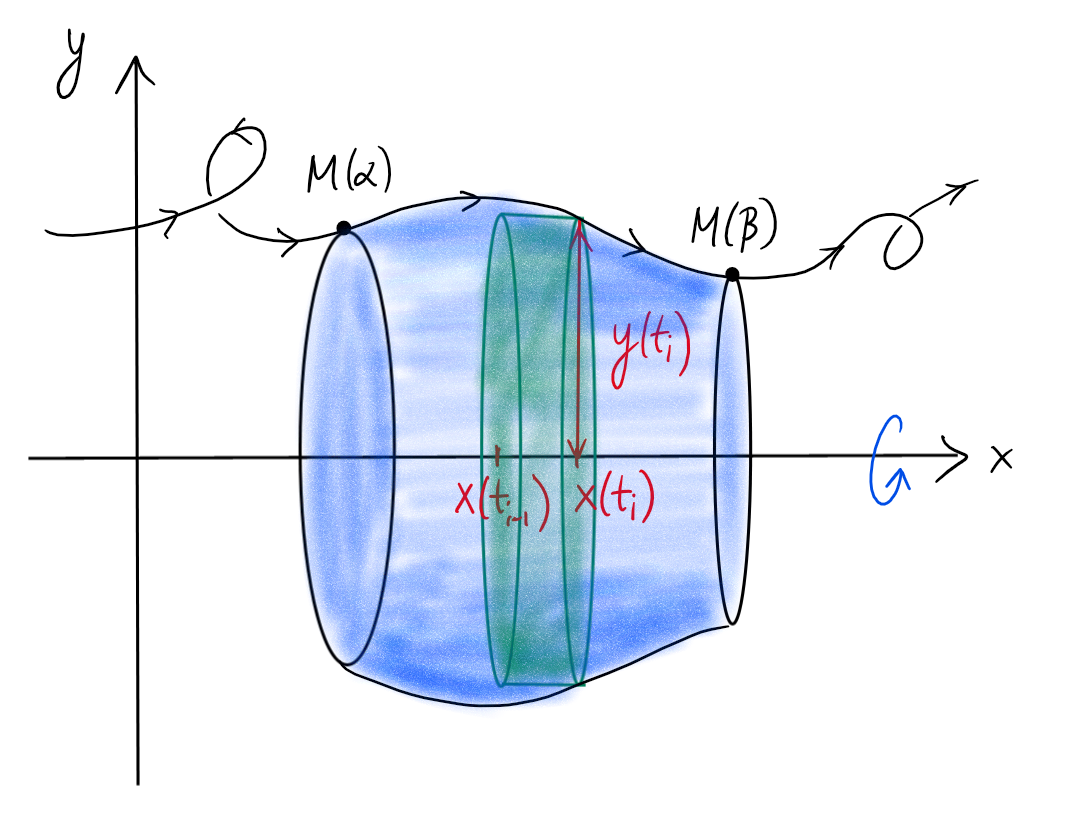
Supposons d'abord que la fonction \(x(t)\) est croissante, c'est-à-dire, que la particule se déplace vers la droite.

En prenant une partition \(\{t_0,t_1,\ldots,t_{n-1},t_n\}\) suffisamment fine de l'intervalle du temps \([\alpha,\beta]\), on a \[\begin{aligned} V &\simeq \sum_{i=1}^n \text{ volume du i-ème cylindre }\\ &=\sum_{i=1}^n \underbrace{\pi \cdot y(t_i)^2}_{\text{base}}\cdot [\underbrace{x(t_i)-x(t_{i-1})}_{\text{hauteur}}]\\ &= \sum_{i=1}^n \pi\cdot y(t_i)^2 \cdot \underbrace{\frac{x(t_i)-x(t_{i-1})}{t_i-t_{i-1}}}_{\simeq \dot{x}(t_i)}\cdot (t_i-t_{i-1}), \end{aligned}\] et si \(x(t)\) est une fonction dérivable avec dérivée continue, on a, dans la limite \(n\to \infty\), \[V=\int_{\alpha}^{\beta} \pi \cdot y(t)^2 \cdot \dot{x}(t) \ dt.\] De manière similaire, si \(x(t)\) est décroissante, on obtient \[V=\int_{\alpha}^{\beta} \pi \cdot y(t)^2 \cdot (-\dot{x}(t)) \ dt.\]

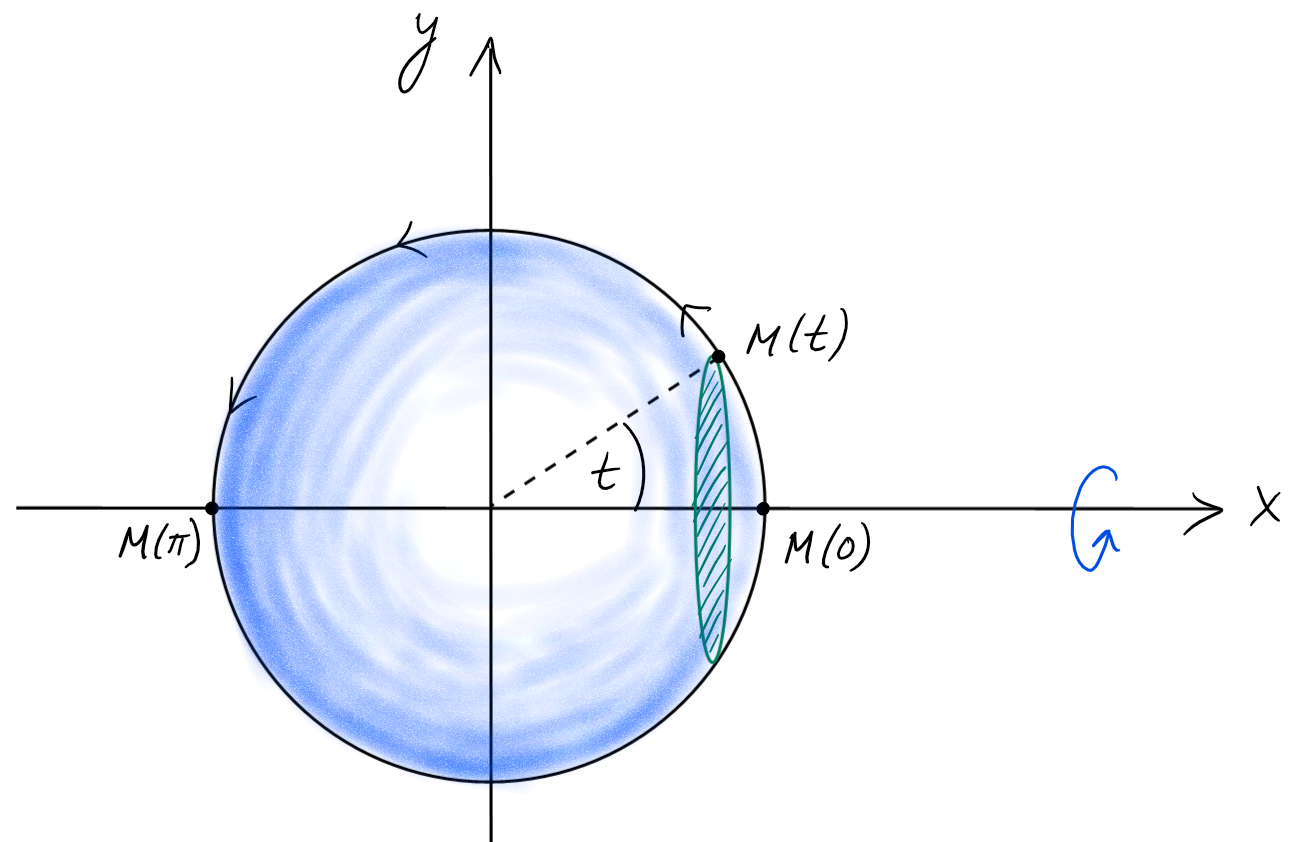
Exemple: La sphère de rayon \(R\) centrée à l'origine est un solide de révolution, puisqu'on peut l'obtenir en faisant tourner un demi-cercle autour de l'axe \(Ox\). Calculons donc son volume \(V\).

Paramétrisons la moitié supérieure du cercle, par exemple avec \[\begin{aligned} M:[0,\pi]&\to \mathbb{R}^2\\ t&\mapsto M(t)=(R\cos(t),R\sin(t)). \end{aligned}\]

Comme \(x(t)=R\cos(t)\) est décroissante sur \([0,\pi]\), le volume est donné par \[\begin{aligned} V&=\int_0^{\pi}\pi \cdot y(t)^2 \cdot (-\dot{x}(t)) \ dt\\ &= \int_0^{\pi}\pi \cdot (R\sin(t))^2 \cdot R\sin(t) \ dt\\ &= \pi R^2\int_0^{\pi} \sin^3(t) \ dt\\ &= -\pi R^2\int_0^{\pi} (1-\cos^2(t))\cdot(-\sin(t))\ dt \end{aligned}\] En posant \(u=\cos(t)\), cette dernière devient \[\begin{aligned} V&= -\pi R^2\int_1^{-1} (1-u^2)\ du\\ &=\pi R^2 \int_{-1}^1 (1-u^2) \ du\\ &=\frac{4\pi R^2}{3}. \end{aligned}\]

---

Dernière compilation: 2024-06-03 (22:36:08)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)