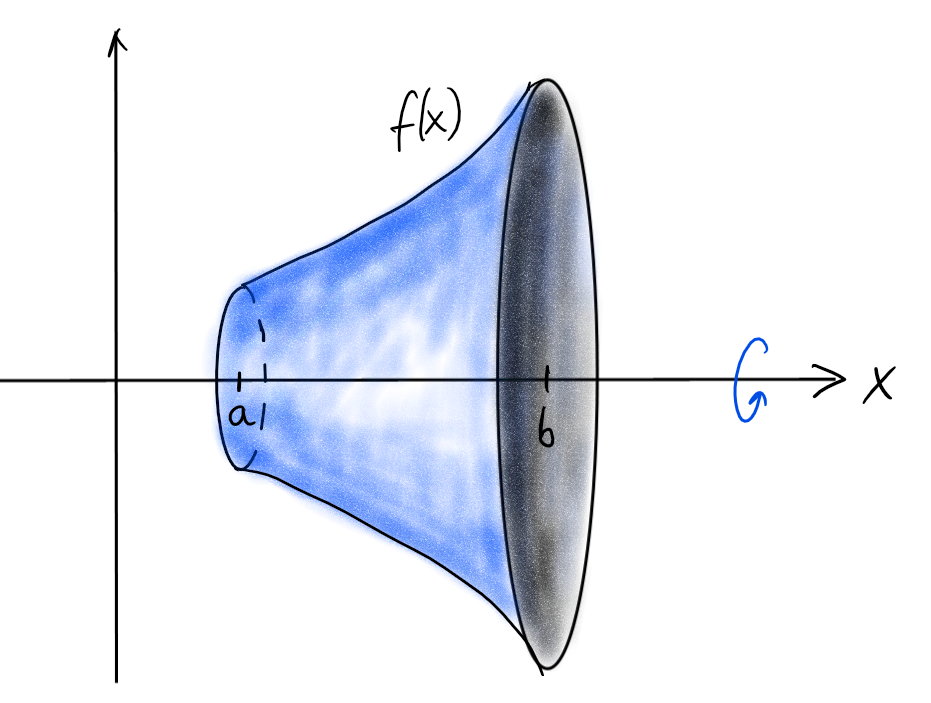
Étant donné une fonction \(f:[a,b]\to \mathbb{R}\), comment calculer l'aire de la surface de révolution engendrée par la rotation du graphe de \(f\) autour de l'axe \(Ox\) ?

Pour commencer, considérons le cas simple où le graphe de \(f\) est un segment de longueur \(\ell\). On appelle bracelet la surface obtenue par la rotation de ce segment autour de \(Ox\):
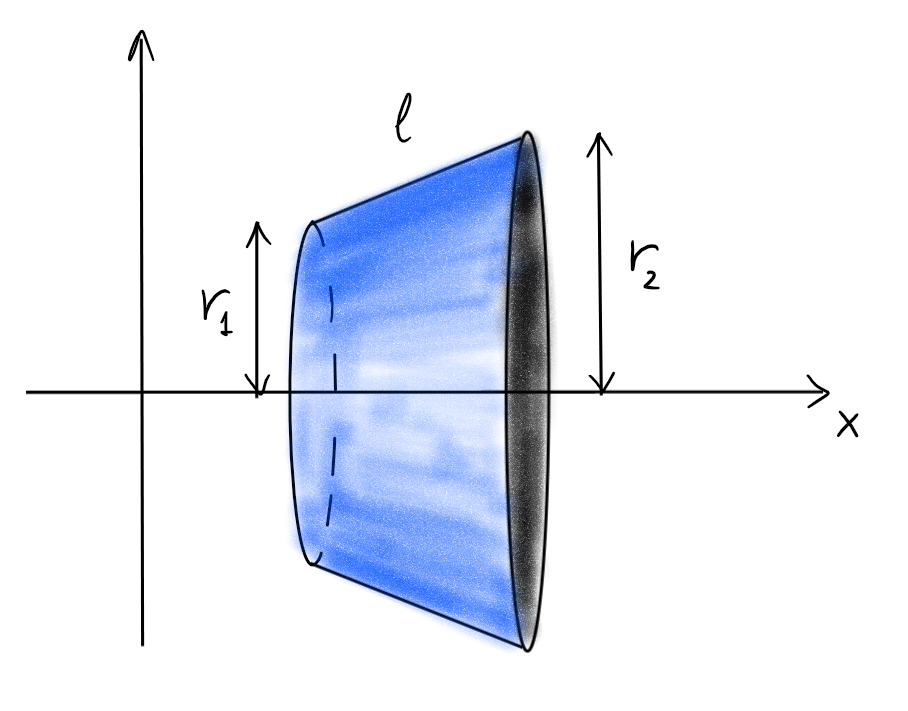
Lemme: L'aire de la surface d'un tel bracelet est donnée par \[2\pi \ell\cdot \left(\frac{r_1+r_2}{2}\right).\]
On remarque que \(\frac{r_1+r_2}{2}\) représente la distance qui sépare le milieu du segment à \(Ox\).
Remarquons que l'aire du bracelet peut être vue comme la différence des aires de deux cônes de bases circulaires, le grand dont le rayon de la base est égal à \(r_2\), le petit dont le rayon de la base est \(r_1\):
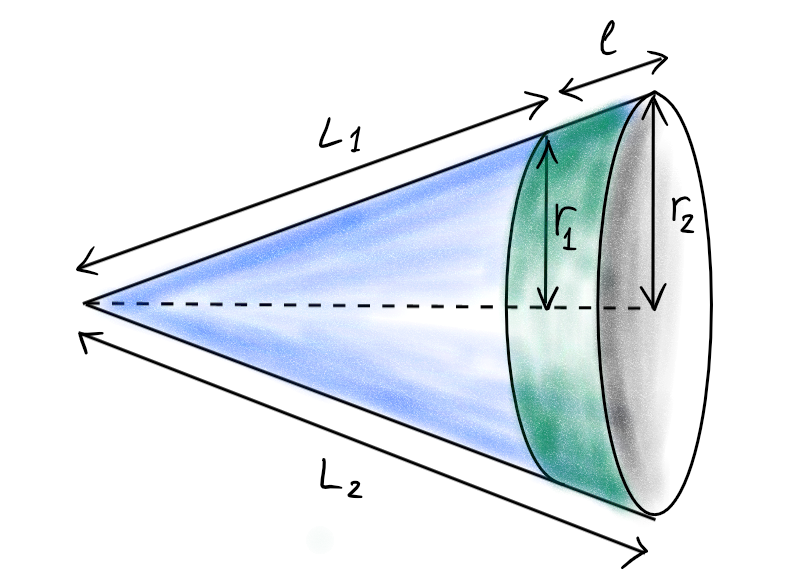
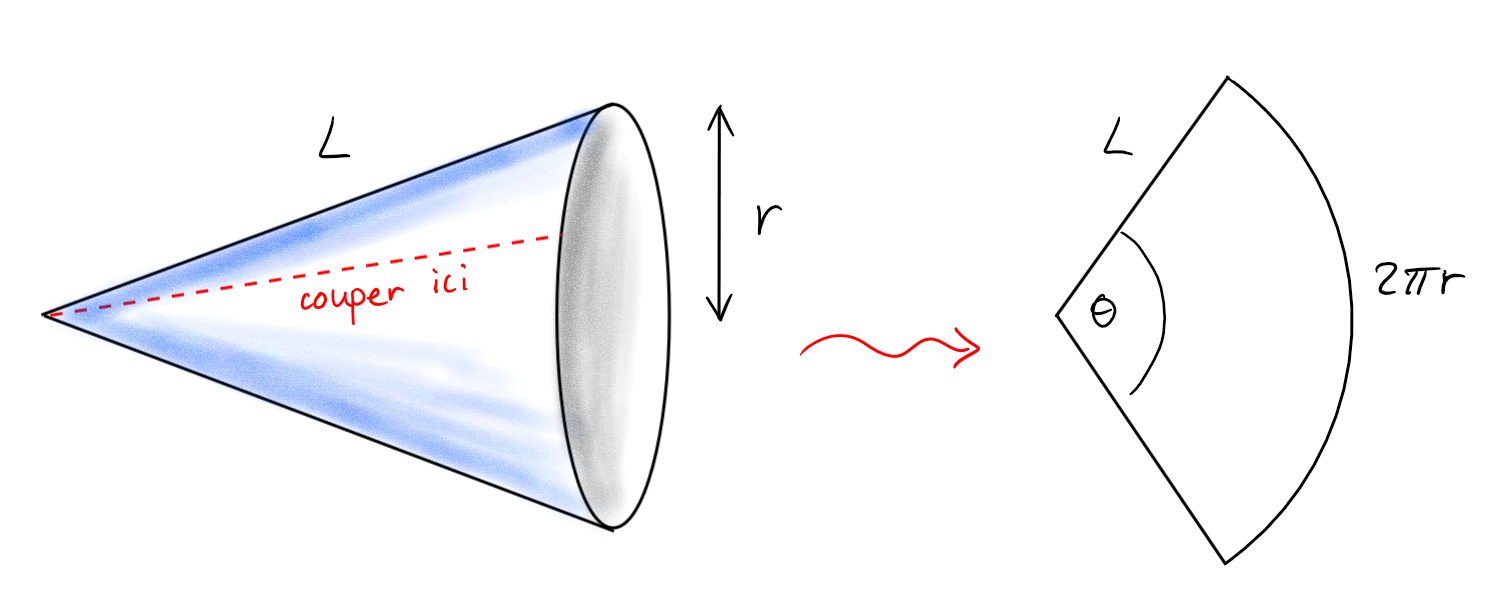
Ayant trouvé l'aire de surface du bracelet, on peut maintenant trouver l'aire
d'une surface de révolution.
On prend une partition \(\{x_0,x_1, x_2, \ldots, x_n\}\) de l'intervalle
\([a,b]\) et on approxime la fonction \(f\) par une fonction linéaire par
morceaux en prenant sur chaque intervalle \([x_{i-1},x_i]\) le segment de droite
entre les points \((x_{i-1},f(x_{i-1}))\) et \((x_i,f(x_i))\). Soit \(L_i\) la
longueur de ce segment.
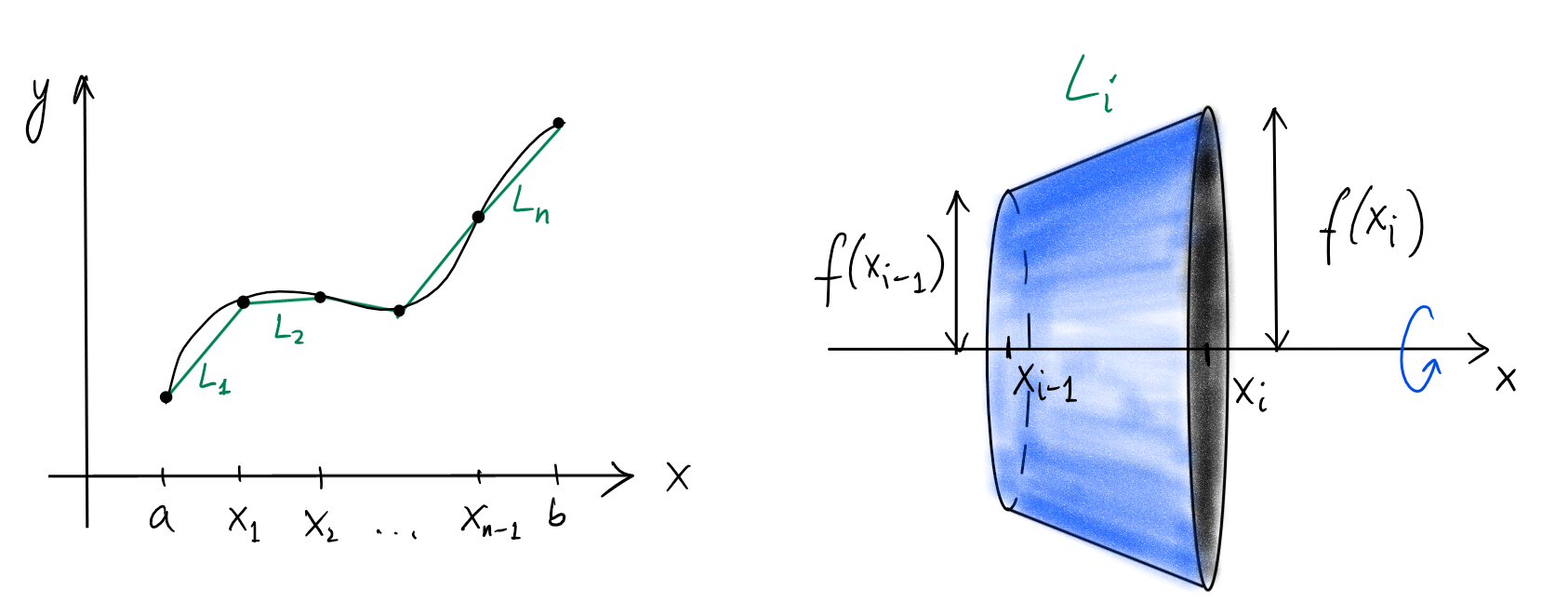
Ainsi, l'aire \(S\) de la surface de révolution est approximée par \[ S \simeq \sum_{i=1}^n S_i, \] où \(S_i\) est l'aire de surface du bracelet obtenu en tournant le \(i\)-ième segment. En utilisant le lemme précédent, on a \[\begin{aligned} S_i &= 2\pi \cdot \frac{f(x_{i-1})+f(x_i)}{2}\cdot L_i\\ &=2\pi \cdot \frac{f(x_{i-1})+f(x_i)}{2}\cdot \sqrt{(x_i-x_{i-1})^2+(f(x_i)-f(x_{i-1}))^2}\\ &=2\pi\cdot \frac{f(x_{i-1})+f(x_i)}{2} \cdot \sqrt{1+\left( \frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} \right)^2}\cdot (x_i-x_{i-1}). \end{aligned}\] Lorsque \(n\) est grand, \[ \frac{f(x_{i-1})+f(x_i)}{2} \simeq f(x_i)\,, \qquad \frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} \simeq f'(x_i) \] Ainsi, dans la limite \(n\to \infty\), la somme tend vers l'intégrale \[S=\int_a^b 2\pi f(x)\sqrt{1+f'(x)^2} \ dx.\]
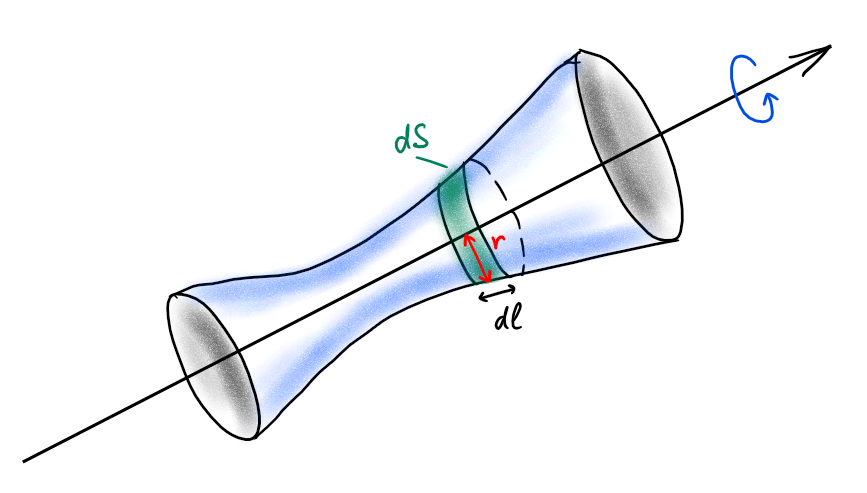
Quel que soit l'axe de révolution, on peut trouver l'aire de surface de révolution de la manière suivante: \[S=\int_a^b dS=\int_a^b 2\pi r \ d\ell,\] où \(r\) est la distance à l'axe de rotation et \(dS=2\pi r \ d\ell\) est le changement infinitésimal d'aire de surface.
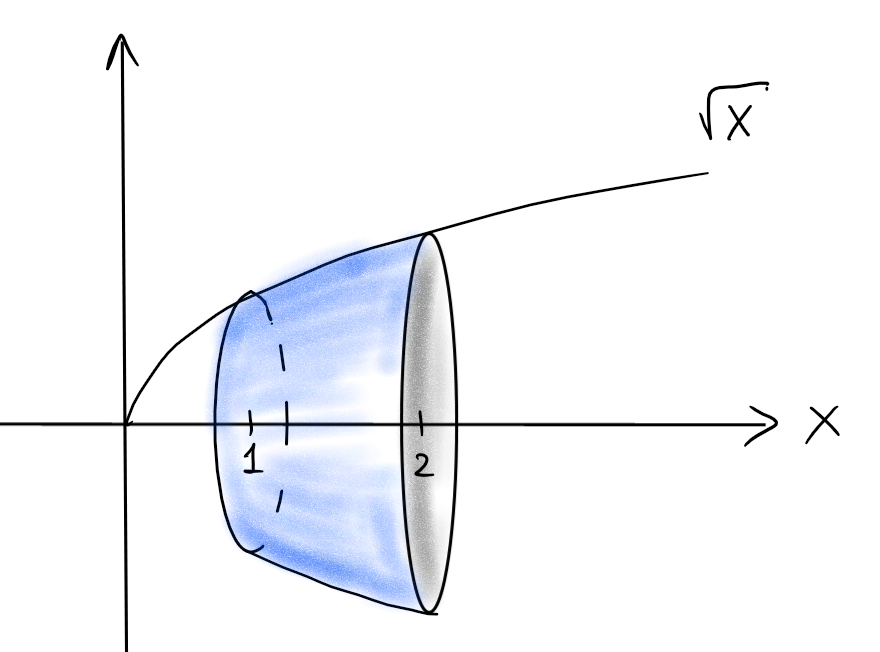
Exemple: Calculons l'aire de surface \(S\) du paraboloïde formé par la rotation de la courbe \(y=\sqrt{x}\) autour l'axe \(Ox\), pour \(x\in[1,2]\).
Soit maintenant \[\begin{aligned} M:[\alpha,\beta]&\to \mathbb{R}^2\\ t&\mapsto M(t)=(x(t),y(t)) \end{aligned}\] une courbe paramétrée, telle que les fonctions \(x(t)\) et \(y(t)\) sont dérivables et dont les dérivées sont continues. De manière analogue au cas d'une fonction standard, on prend une partition \(\{t_0, t_1, \ldots t_n\}\) de l'intervalle \([\alpha, \beta]\) et on approxime la courbe en prenant sur chaque intervalle \([t_{i-1},t_i]\) le segment de droite entre les points \(M(t_{i-1})\) et \(M(t_i)\). Soit \(L_i\) la longueur de ce segment.
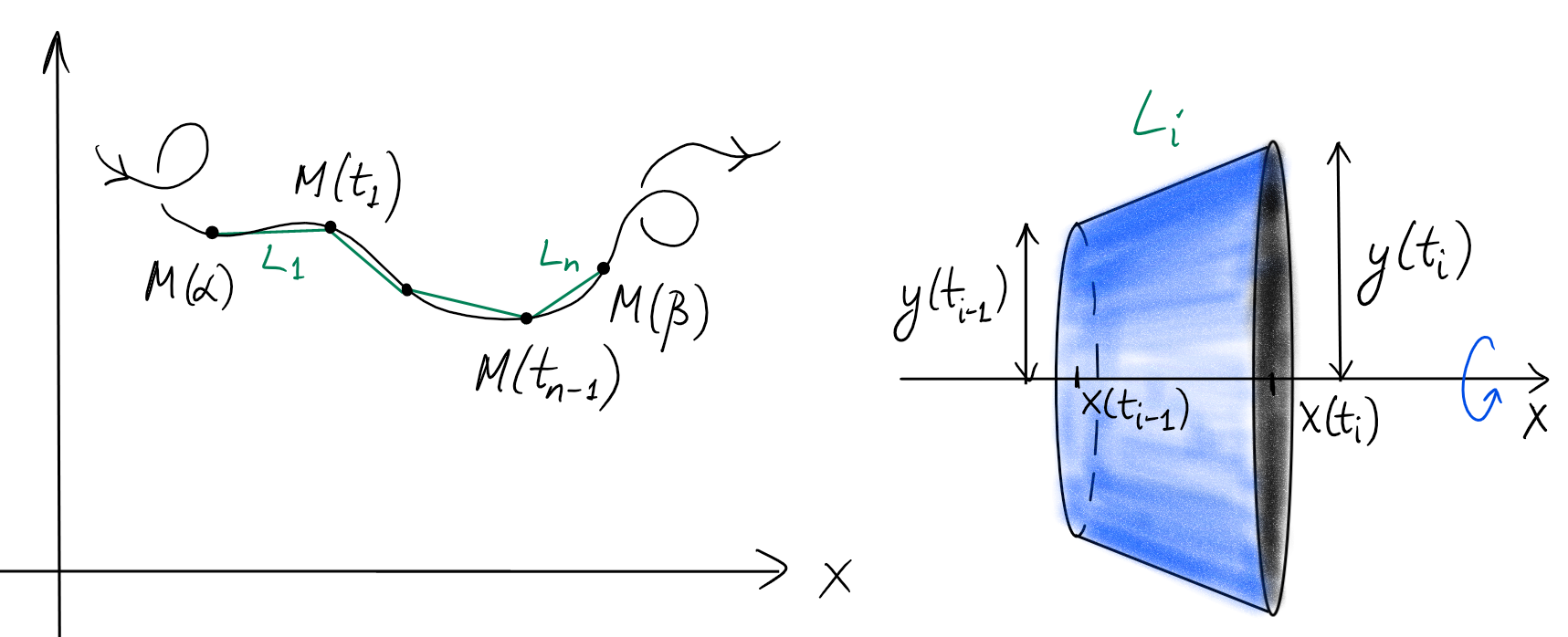
Ainsi, l'aire de la surface de révolution \(S\) est approximée par
\[S\simeq \sum_{i=1}^n S_i,\]
où \(S_i\) est l'aire de surface du \(i\)-ième bracelet.
On a
\[\begin{aligned}
S_i
&= 2\pi\cdot \frac{y(t_{i-1})+y(t_i)}{2}\cdot L_i\\
&= 2\pi \cdot \frac{y(t_{i-1})+y(t_i)}{2}\cdot
\sqrt{(x_(t_i)-x(t_{i-1}))^2+(y_(t_i)-y(t_{i-1}))^2}\\
&= 2\pi \cdot \frac{y(t_{i-1})+y(t_i)}{2}\cdot
\sqrt{\left(\frac{x_(t_i)-x(t_{i-1})}{t_i-t_{i-1}}
\right)^2+\left(\frac{y_(t_i)-y(t_{i-1})}{t_i-t_{i-1}}
\right)^2}\cdot (t_i-t_{i-1})\,.
\end{aligned}\]
En prenant la limite \(n\to \infty\), la somme tend vers l'intégrale
\[S=\int_{\alpha}^{\beta} 2\pi y(t) \sqrt{\dot{x}(t)^2+\dot{y}(t)^2} \ dt\]
On remarque qu'en prenant le vecteur tangent
\[\dot{\vec{r}}(t)=
\begin{pmatrix}
\dot{x}(t)\\
\dot{y}(t)
\end{pmatrix},\]
la formule ci-dessus devient
\[S=\int_{\alpha}^{\beta} 2\pi y(t) \|\dot{\vec{r}}(t)\| \ dt.\]
On remarque qu'en faisant la rotation autour de l'axe \(Oy\), les rôles de \(x(t)\) et \(y(t)\) seront inversés.