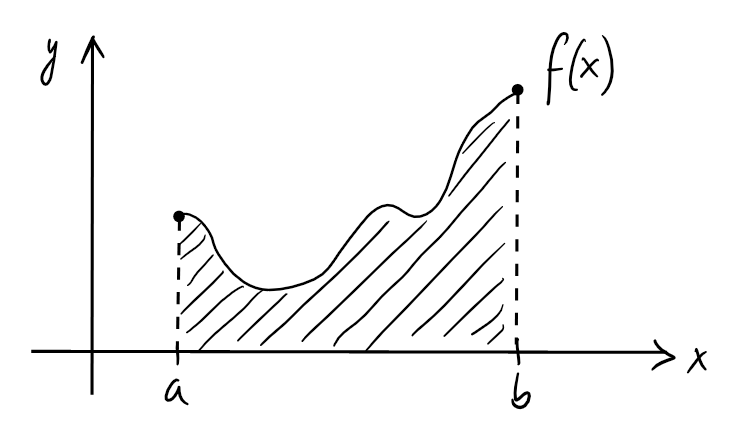
7.1 Construction de l'intégrale Riemann--Darboux

On sait, depuis les cours de géométrie plane élémentaire, comment calculer des aires de régions simples, telles que rectangles, triangles ou disques.

Comment faire pour calculer des aires de régions plus compliquées, comme par exemple l'aire sous le graphe d'une fonction?

Le calcul intégral, que nous allons développer dans ce chapitre, permet dans certains cas de répondre à cette question.

Mais avant de vouloir la calculer, il faut définir précisément l'aire sous le graphe d'une fonction.

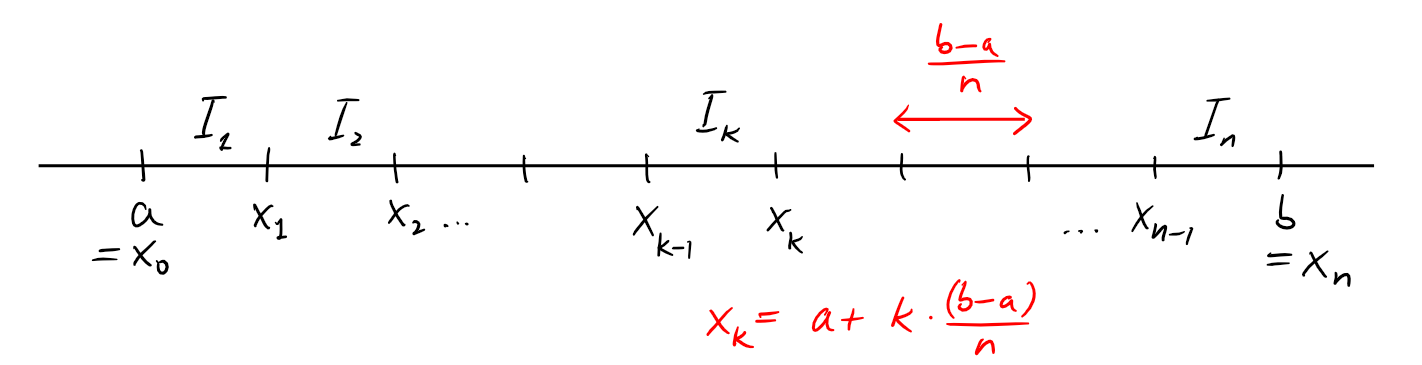
Soit \(n\geqslant 1\) un entier. La subdivision (ou partition) régulière (à \(n\) éléments) de l'intervalle \([a,b]\) est la division de \([a,b]\) en \(n\) sous-intervalles de longueurs égales, \(I_k=[x_{k-1},x_k]\), \(k=1,2,\dots,n\), où \[ x_k=a+k\frac{b-a}{n}\,,\qquad k=0,1,2,\dots,n\,. \]

Soient, pour \(k=1,2,\dots,n\), \[\begin{aligned} m_k&:=\min_{x\in I_k} f(x)\\ M_k&:=\max_{x\in I_k} f(x). \end{aligned}\] Ces nombres sont bien définis puisque \(f\) est supposée continue.

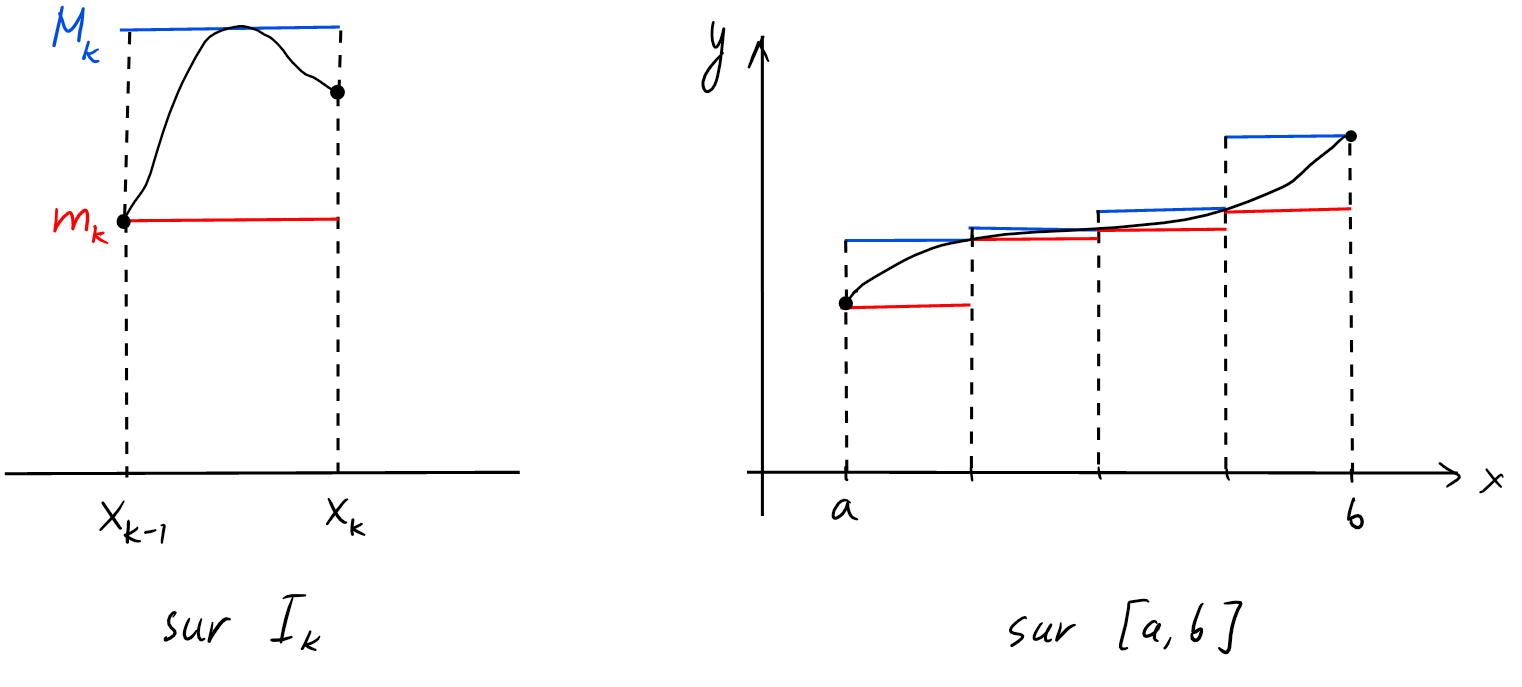
On définit la somme de Darboux inférieure \[s_n :=\sum_{k=1}^{n}\frac{b-a}{n} \cdot m_k,\] et la somme de Darboux supérieure \[S_n :=\sum_{k=1}^{n}\frac{b-a}{n}\cdot M_k,\] D'un point de vue géométrique, pour une fonction prenant des valeurs positives sur \([a,b]\), la somme de Darboux inférieure (resp. supérieure) représente une somme d'aires de \(n\) rectangles, tous de base égale à \(\frac{b-a}{n}\), dont les côtés supérieurs sont tous situés au-dessous (resp. au-dessus) du graphe de \(f\). Pour une partition contenant beaucoup de points, on s'attend à ce que \(s_n\) et \(S_n\) soient proches l'une de l'autre et tendent vers une même limite:

On peut effectivement garantir que ceci a lieu lorsque la fonction est continue:

Théorème: Si \(f:[a,b]\to \mathbb{R}\) est continue alors les suites \((s_n)\) et \((S_n)\) sont convergentes, et possèdent la même limite. Cette limite commune est appelée l'intégrale de \(f\), on la note \[ \int_a^b f(x) \, dx :=\lim_{n\to \infty} s_n =\lim_{n\to \infty} S_n\,. \]

En fait, on peut montrer que \(\lim_{n\to \infty} s_n=\lim_{n\to \infty} S_n\) même si \(f\) possède un nombre fini de discontinuités; dans de tels cas l'intégrale \(\int_a^bf(x)\,dx\) est aussi bien définie.

L'intégrale définie ci-dessus est ce qu'on appelle l'intégrale définie (on parlera d'intégrale indéfinie plus tard).

Exemple: Soit \(f(x)=x\). Calculons l'aire \(A\) de la région délimitée par l'axe \(Ox\) et le graphe de \(f\), entre \(a=0\) et un point \(b\gt 0\). (Puisque cette région est un triangle, on sait qu'on doit trouver \(A=\frac12 \cdot b \cdot x\).)

Il s'agit donc de calculer \[ \int_0^b x \, dx\,. \] Comme \(f(x)\) est continue, on peut calculer cette intégrale à partir de sa définition, avec \(\lim_{n\to\infty}s_n\) ou \(\lim_{n\to\infty}S_n\).

Fixons \(n\geqslant 1\) et calculons la somme inférieure \(s_n\) de \(f\) sur l'intervalle \([0,b]\).

Comme \(f\) est croissante sur \([0,b]\), elle est croissante sur chaque intervalle \(I_k=[x_{k-1},x_k]\), et donc \[\begin{aligned} M_k&=\max_{x\in I_k} f(x)=f(x_{k})\,,\\ m_k&=\min_{x\in I_k} f(x)=f(x_{k-1})\,. \end{aligned}\] Puisque \(x_k=0+k\cdot\frac{b-0}{n}=\frac{kb}{n}\), \[\begin{aligned} s_n &= \sum_{k=1}^n \frac{b-0}{n} m_k\\ &= \frac{b}{n}\sum_{k=1}^n f(x_{k-1})\\ &= \frac{b}{n}\sum_{k=1}^n f \left( \frac{b(k-1)}{n} \right)\\ &= \frac{b}{n}\sum_{k=1}^n \frac{b(k-1)}{n} \quad (\text{ par définition de } f)\\ &= \frac{b^2}{n^2} \sum_{k=1}^n (k-1)\\ &= \frac{b^2}{n^2} \sum_{j=1}^{n-1}j\\ \end{aligned}\] où on a fait le changement \(j:= k-1\).

Or on sait (voir Analyse A) que \[ \sum_{j =1}^N j = 1+2+3+\cdots N =\frac{N(N+1)}{2}\,. \] En appliquant cette formule avec \(N=n-1\), \[ \sum_{j=1}^{n-1} j =\frac{(n-1)n}{2}\,. \] On a donc \[ s_n = \frac{b^2}{n^2}\cdot \frac{n(n-1)}{2} =\frac{b^2(n-1)}{2n}\,, \] ce qui implique que \[\begin{aligned} \int_0^1 x \ dx &= \lim_{n\to \infty} s_n\\ &= \lim_{n\to \infty} \frac{b^2(n-1)}{2n}=\frac{b^2}{2}\,. \end{aligned}\]

Exemple: Soit \(f(x)=1-x^2\). Calculons l'aire \(A\) de la région délimitée par l'axe \(Ox\) et le graphe de \(f(x)\).

Par la parité de \(f\), on a \[ \int_{-1}^1 f(x) \ dx =2\int_0^1 f(x) \, dx\,. \] Comme \(f\) est continue, on peut calculer cette deuxième intégrale, \(\int_0^1 f(x) \, dx\), à partir de sa définition, avec \(\lim_{n\to\infty}s_n\) ou \(\lim_{n\to\infty}S_n\).

Fixons \(n\geqslant 1\) et calculons la somme supérieure \(S_n\) de \(f\) sur l'intervalle \([0,1]\).

Comme \(f\) est décroissante sur \([0,1]\), elle est décroissante sur chaque intervalle \(I_k=[x_{k-1},x_k]\), et donc \[\begin{aligned} M_k&=\max_{x\in I_k} f(x)=f(x_{k-1})\,,\\ m_k&=\min_{x\in I_k} f(x)=f(x_k)\,. \end{aligned}\] Puisque \(x_k=0+k\cdot\frac{1-0}{n}=\frac{k}{n}\), \[\begin{aligned} S_n &= \sum_{k=1}^n \frac{1-0}{n} M_k\\ &= \frac{1}{n}\sum_{k=1}^n f(x_{k-1})\\ &= \frac{1}{n}\sum_{k=1}^n f\left(\frac{k-1}{n}\right)\\ &= \frac{1}{n}\sum_{k=1}^n \left(1-\left(\frac{k-1}{n}\right)^2\right) \quad (\text{ par définition de } f)\\ &= \frac{1}{n}\left[n-\frac{1}{n^2} \sum_{k=1}^n (k-1)^2 \right]\\ &= \frac{1}{n}\left[n-\frac{1}{n^2} \sum_{j=1}^{n-1} j^2 \right]\,, \end{aligned}\] où on a fait le changement \(j:= k-1\).

Or on sait (voir Analyse A) que \[ \sum_{j =1}^N j^2 = 1^2+2^2+3^2+\cdots N^2 =\frac{N(N+1)(2N+1)}{6}\,. \] En appliquant cette formule avec \(N=n-1\), \[ \sum_{j=1}^{n-1} j^2 =\frac{(n-1)n[2(n-1)+1]}{6} =\frac{n(n-1)(2n-1)}{6}\,. \] On a donc \[ S_n = \frac{1}{n}\left[ n- \frac{n(n-1)(2n-1)}{6n^3}\right] =1-\frac{n(n-1)(2n-1)}{6n^3}\,, \] ce qui implique que \[\begin{aligned} \int_0^1f(x) \ dx &= \lim_{n\to \infty} S_n\\ &= \lim_{n\to \infty} \left[1-\frac{n(n-1)(2n-1)}{6n^3}\right]\\ &= 1-\frac{2}{6}\\ &=\frac{2}{3}\,. \end{aligned}\] Finalement, \[ \int_{-1}^1 f(x) \ dx = 2\cdot \frac{2}{3} =\frac{4}{3} \]

Dernière compilation: 2024-06-03 (22:36:08)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)