Analyse B (MAN)

7.2 Propriétés de l'intégrale

Dans cette section, on donne les principales propriétés de l'intégrale. Notons que la définition d'intégrale, donnée dans la section précédente, est une version légèrement simplifiée en comparaison de celle trouvée généralement dans les textes d'analyse, et que certaines des propriétés ci-dessous, pour pouvoir être démontrées rigoureusement, requièrent une définition un peu plus générale.

Pour des raisons de commodité, commençons par définir \[ \int_a^a f(x) \ dx:=0\,. \] Ci-dessous, nous supposerons partout que \(f\) est une fonction continue sur un intervalle \([a,b]\).

Relation de Chasles: si \(a\lt c\lt b\), \[ \int_a^c f(x) \, dx + \int_c^b f(x) \, dx = \int_a^b f(x) \, dx\,. \] Afin que la relation de Chasles reste valable pour un triplet quelconque \(a,b,c\), on peut définir \[ \int_b^a f(x) \, dx:=-\int_a^b f(x) \, dx \] Ceci permer d'écrire \[ \int_a^b f(x) \, dx + \int_b^a f(x) \, dx = \int_a^a f(x) \, dx=0\,. \]
Linéarité: Si \(g\) est aussi continue sur \([a,b]\), et si \(\lambda, \mu\) sont deux constantes réelles, alors \[ \int_a^b (\lambda f(x)+\mu g(x)) \, dx =\lambda\int_a^b f(x) \, dx + \mu \int_a^b g(x) \, dx\,. \]
Inégalités: Si \(f(x)\leqslant g(x)\) pour tout \(x\in [a,b]\), alors \[ \int_a^b f(x) \, dx \leqslant \int_a^b g(x) \, dx\,. \]
Preuve:

Notons \(S_n^f\) et \(S_n^g\) les sommes de Darboux supérieures associées à \(f\) et \(g\): \[ S_n^f=\sum_{k=1}^n\frac{b-a}{n}M_k^f\,,\qquad S_n^g=\sum_{k=1}^n\frac{b-a}{n}M_k^g\,. \] Puisque \(f(x)\leqslant g(x)\) pour tout \(x\in [a,b]\), on a en particulier que pour chaque \(k=1,2,\dots,n\), \[ M_k^f =\max_{x\in I_k}f(x) \leqslant\max_{x\in I_k}g(x) =M_k^g\,. \] Ainsi, \(S_n^f\leqslant S_n^g\), et donc \[\begin{aligned} \int_a^b f(x) \, dx &=\lim_{n\to\infty}S_n^f\\ &\leqslant \lim_{n\to\infty}S_n^g\\ &= \int_a^b g(x) \, dx\,. \end{aligned}\]
Une conséquence: \[ \left| \int_a^b f(x) \ dx \right| \leqslant \int_a^b |f(x)| \ dx\,. \]
Preuve:

Puisque \[ -|f(x)|\leqslant f(x) \leqslant |f(x)| \quad \forall x\in [a,b]\,, \] l'inégalité du dessus implique que \[ \underbrace{-\int_a^b |f(x)| \ dx}_{-B} \leqslant \underbrace{\int_a^b f(x) \ dx}_{A} \leqslant \underbrace{\int_a^b |f(x)| \ dx}_{B}\,. \] On déduit que \(|A|\leqslant B\).
Si \(f\) est paire sur \([-a,a]\), alors \[ \int_{-a}^a f(x) \, dx=2\int_0^a f(x) \ dx\,. \]
Si \(f\) est impaire sur \([-a,a]\), alors \[ \int_{-a}^a f(x) \, dx=0\,. \]

Le Théorème de la moyenne

Théorème: Si \(f:[a,b]\rightarrow \mathbb{R}\) est continue, alors il existe \(c\in ]a,b[\) tel que \[\int_a^b f(x) \ dx=f(c)\cdot (b-a).\]

Preuve:

Comme \(f\) est continue, elle atteint son minimum et son maximum sur \([a,b]\): \[ m:=\min_{x\in [a,b]}f(x)\,,\qquad M:=\max_{x\in [a,b]}f(x)\,. \] Ainsi, \(m\leqslant f(x) \leqslant M\) pour tout \(x\in [a,b]\). \[ \underbrace{\int_a^b m \ dx}_{=m\cdot(b-a)} \leqslant \int_a^b f(x) \ dx \leqslant \underbrace{\int_a^b M \ dx}_{=M\cdot(b-a)}\,. \] En divisant par \(b-a\), on obtient \(m\leqslant \overline{f} \leqslant M\). Par le Théorème des valeurs intermédiaires, il existe \(c\in ]a,b[\) tel que \(f(c)=\overline{f}\).

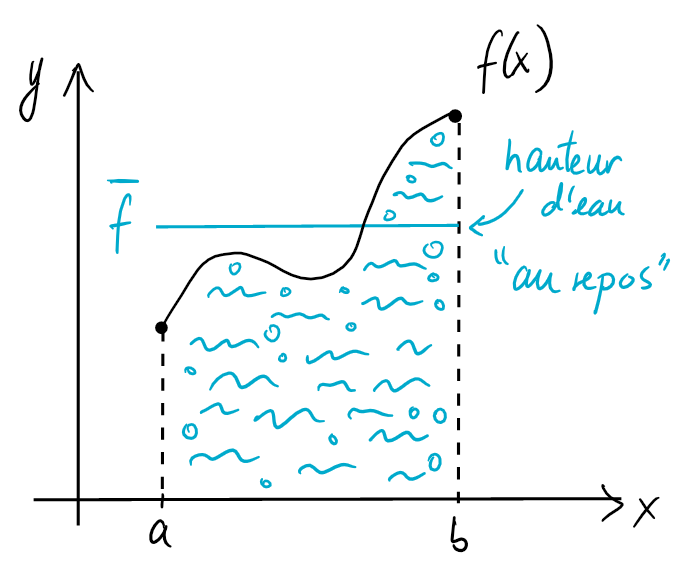
Pour trouver la moyenne des nombres \(y_1,y_2,\ldots y_n\), on prend la somme \(y_1+y_2+\cdots y_n\) et on divise par \(n\). Étant donné une fonction \(f\), l'analogue serait de prendre l'intégrale de \(f\) sur \([a,b]\) et divise par la longueur de l'intervalle, \(b-a\). Ainsi, la quantité \[ \overline{f}:=\frac{1}{b-a} \int_a^b f(x) \ dx \] représente la moyenne de la fonction sur l'intervalle \([a,b]\).

On a donc \(\int_a^b f(x) \ dx=\overline{f}\cdot (b-a)\), et le Théorème de la moyenne affirme qu'il existe un \(c\in ]a,b[\) tel que \(f(c)=\overline{f}\).