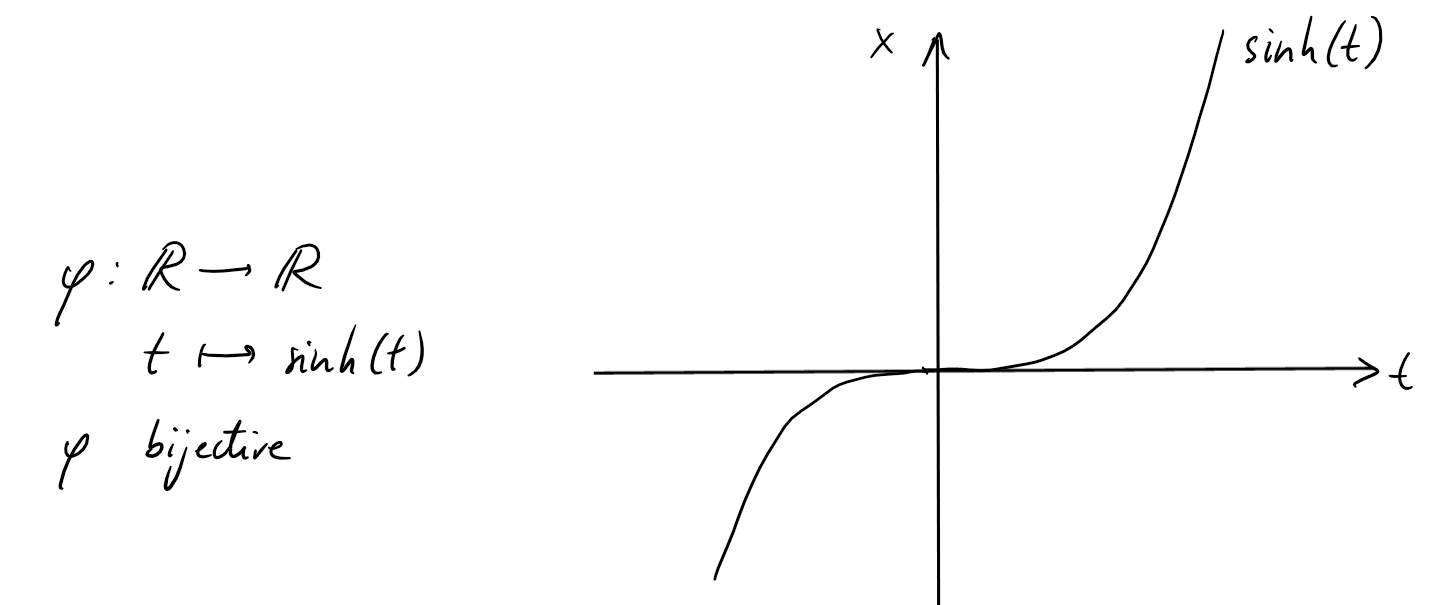7.8 Changement de variable: fonctions trigonométriques

Dans la sous-section précédente, on a défini une nouvelle variable en fonction de l'ancienne: \(u=g(x)\).

On peut aussi exprimer l'ancienne variable en fonction d'une nouvelle: \(x=\varphi(t)\). Si \(\varphi\) est bijective (et donc inversible), alors \(t=\varphi^{-1}(x)\), et donc si on trouve que \[ \int f(x) \ dx = \int f(\varphi(t))\varphi'(t) \ dt = H(t)+C\,, \] pour une certaine fonction \(H\), on a alors \[ \int f(x) \, dx =H(\varphi^{-1}(x))+C\,. \]

Exemple: Considérons \[ \int \sqrt{1-x^2} \ dx\,,\qquad x\in [-1,1]\,. \] Si \(1-x^2\) était un carré, \(y^2\), ce serait plus facile d'intégrer. Mais \[ 1-x^2=y^2 \iff x^2+y^2=1 \,, \] c'est-à-dire si \((x,y)\) est sur le cercle unité. Ceci suggère d'introduire une variable d'angle \(t\), et de faire la substitution \[ x=\varphi(t)=\cos(t)\,\quad t\in [0,\pi]\,. \] Remarquons que \(\varphi:[0,\varphi]\to[-1,1]\) est bijective, et que sa réciproque est \(t=\varphi^{-1}(x)=\arccos(x)\). Puisque \(\varphi'(t)=-\sin(t)\), \[\begin{aligned} \int \sqrt{1-x^2} \ dx &= \int \sqrt{1-\cos^2(t)} (-\sin(t)) \ dt\\ &= \int \sin(t) (-\sin(t)) \ dt\\ &= -\int \sin^2(t) \ dt\,. \end{aligned}\] Dans la dernière égalité, on a utilisé le fait que \(\sin(t)\geqslant 0\) puisque \(t\in [0,\pi]\)).

Ensuite, on a vu plus haut que \[\begin{aligned} -\int \sin^2(t) \, dt &=\underbrace{-\frac{1}{2} t +\frac{1}{4} \sin(2t)}_{H(t)} +C\\ &=-\frac{1}{2} t+\frac{1}{2} \sin(t)\cos(t)+C\,. \end{aligned}\] On a donc: \[\begin{aligned} \int \sqrt{1-x^2} \, dx =-\frac{1}{2}\arccos(x)+\frac{1}{2}x\sqrt{1-x^2}+C. \end{aligned}\]

Plus généralement, si la fonction à intégrer contient \[\sqrt{a^2-b^2 x^2},\] \(a,b\in \mathbb{R}\) constantes, on peut essayer un changement de variable de la forme \[x=\frac{a}{b}\cos(t) \quad \text{ ou } \quad x=\frac{a}{b}\sin(t).\] Notons que pour la substitution \(x=\frac{a}{b}\sin(t)\), il faut que \(t\in \left[\frac{-\pi}{2},\frac{\pi}{2}\right]\) pour que \(\varphi(t):=\sin(t)\) soit bijective.

Exemples:

Les prochains exemples utilisent les fonctions hyperboliques \(\cosh(t)\) et \(\sinh(t)\). De manière analogue aux fonctions trigonométriques \(\cos(t)\) et \(\sin(t)\) qui paramétrisent le cercle unité \(x^2+y^2=1\), les fonctions hyperboliques donnent une paramétrisation \(x=\cosh(t)\), \(y=\sinh(t)\) de l'hyperbole unité \(x^2-y^2=1\).

Exemple: \(\int \sqrt{1+x^2} \ dx\), \(x\in \mathbb{R}\).

De nouveau, si \(1+x^2\) était un carré, \(y^2\), ce serait plus facile à intégrer. On a l'identité \[\cosh^2(x)-\sinh^2(x)=1,\] et donc on peut poser \(x=\sinh(t)\), \(t\in \mathbb{R}\). Ainsi, \(\sqrt{1+x^2}=\sqrt{1+\sinh^2(t)}=\sqrt{\cosh^2(t)}=\cosh(t)\), \(dx = \cosh(t) \ dt\) et \(t=\mathrm{argsinh }(x)\).

On a \[\begin{aligned} \int \sqrt{1+x^2} \ dx &= \int \cosh(t) \cdot \cosh(t) \ dt\\ &= \int \cosh^2(t) \ dt\\ &= \int \left[ \frac{e^t+e^{-t}}{2} \right]^2 \ dt\\ &=\frac{1}{4} \int (e^{2t}+2+e^{-2t}) \ dt\\ &=\frac{1}{4} (\frac{1}{2}e^{2t}+2t-\frac{1}{2}e^{-2t})+C\\ &=\frac{1}{4}\left(2t+\frac{e^{2t}-e^{-2t}}{2}\right)+C\\ &=\frac{1}{4}[2t+\sinh(2t)]+C\\ &=\frac{1}{4}[2t +2\sinh(t)\cdot \cosh(t)] +C\\ &=\frac{1}{4}\left[2\mathrm{argsinh }(x)+2x\sqrt{1+x^2}\right]+C. \end{aligned}\]

Plus généralement, si la fonction à intégrer contient \[\sqrt{a^2+b^2 x^2},\] \(a,b\in \mathbb{R}\) constantes, on peut essayer un changement de variable de la forme \[x=\frac{a}{b}\sinh(t).\] Ce changement donnerait \[\sqrt{a^2+b^2 x^2}=\sqrt{a^2+b^2\left(\frac{a}{b}\sinh(t)\right)^2}=\sqrt{a^2(1+\sinh^2(t))}=|a|\cdot\cosh(t).\]

Exemple: \(\int \sqrt{x^2-1} \ dx\).

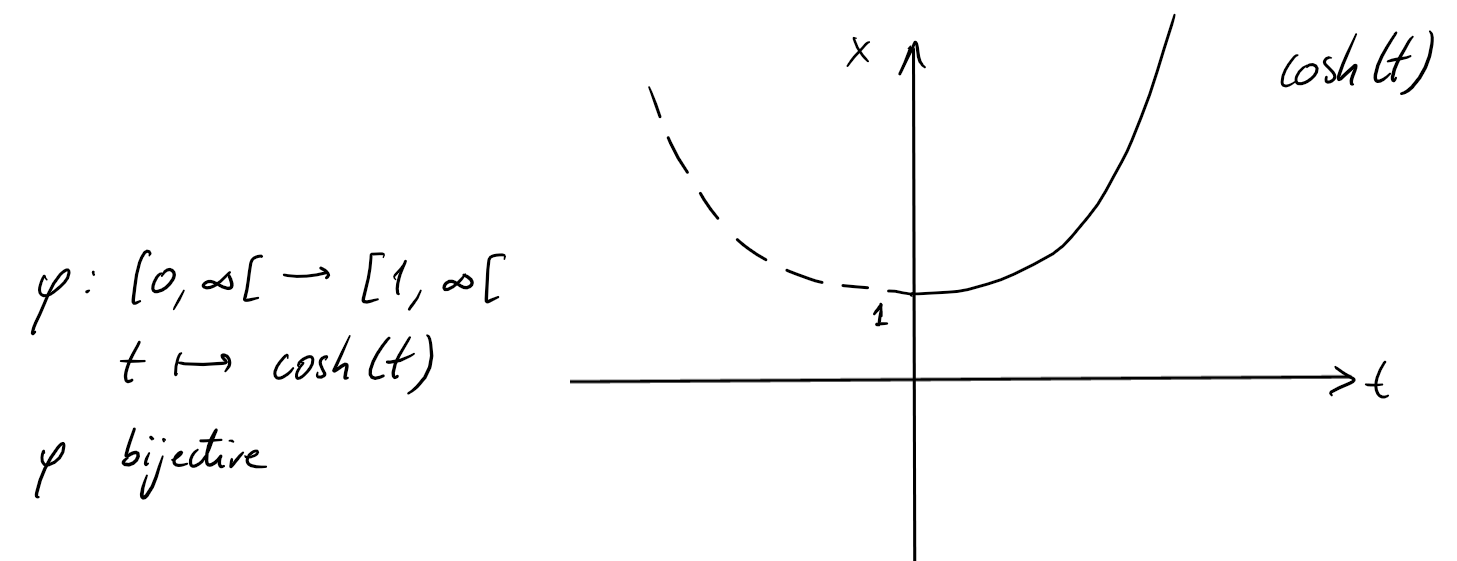
Ici, l'intégrande est définie pour \(x\in ]-\infty,-1]\cup [1,+\infty[\). Comme dans l'exemple précédent, on peut utiliser l'identité \[\cosh^2(x)-\sinh^2(x)=1.\] Si \(x\geqslant 1\):

On peut poser \(x=\cosh(t), t\geqslant 0\). Ainsi, \(\sqrt{x^2-1}=\sqrt{\cosh^2(t)-1}=\sqrt{\sinh^2(t)}=|\sinh(t)|=\sinh(t)\) (car \(t\geqslant 0\)), \(dx = \sinh(t) \ dt\) et \(t=\mathrm{argcosh }(x)\).

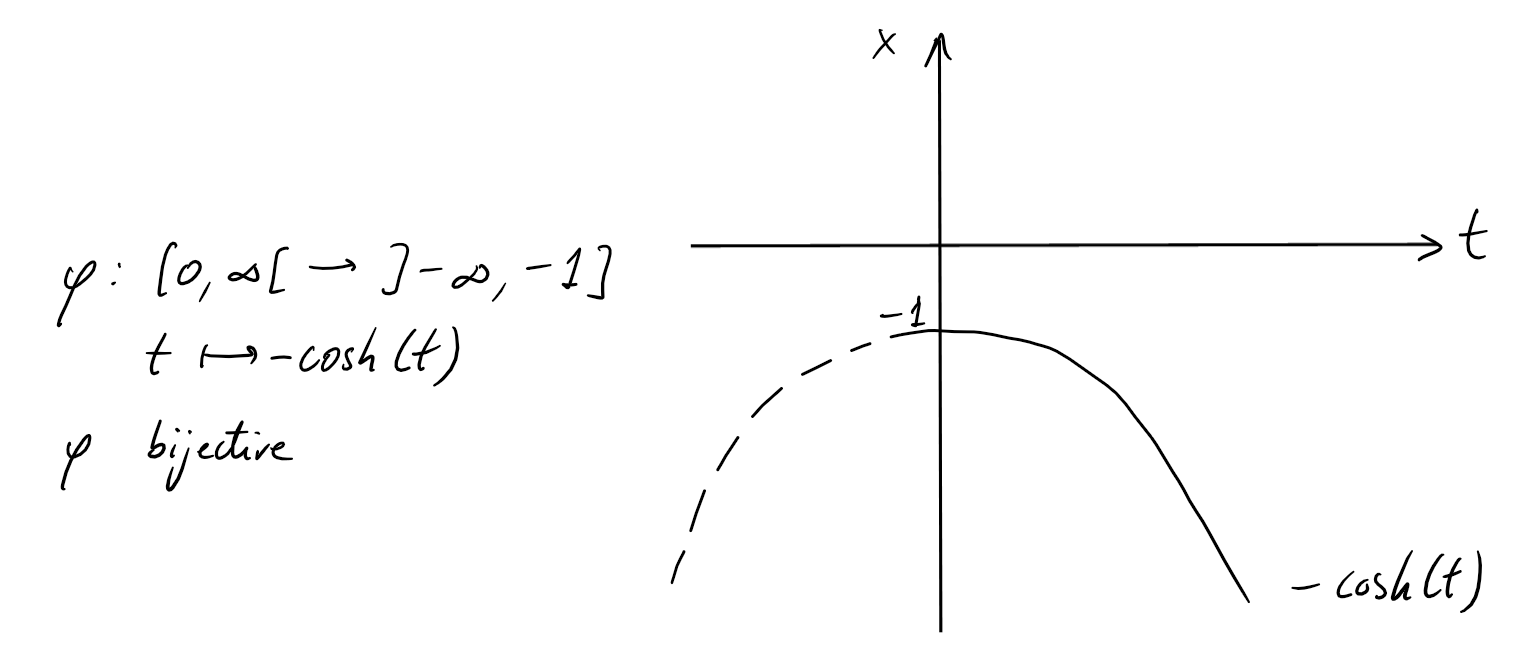
On a \[\begin{aligned} \int \sqrt{x^2-1} \ dx &= \int \sinh^2(t) \ dt\\ &= \cdots\\ &=-\frac{1}{2}\mathrm{argcosh }(x)+\frac{1}{2}x\sqrt{x^2-1} +C. \end{aligned}\] Si \(x\leqslant -1\):

On peut poser \(x=-\cosh(t), t\geqslant 0\). Ainsi, \(\sqrt{x^2-1}=\sqrt{(-\cosh(t))^2-1}=\sqrt{\sinh^2(t)}=|\sinh(t)|=\sinh(t)\) (car \(t\geqslant 0\)), \(dx = -\sinh(t) \ dt\) et \(t=\mathrm{argcosh }(-x)\).
On a \[\begin{aligned} \int \sqrt{x^2-1} \ dx &= \int -\sinh^2(t) \ dt\\ &=\cdots\\ &=\frac{1}{2}\mathrm{argcosh }(-x)+\frac{1}{2}x\sqrt{x^2-1} +C. \end{aligned}\] En résumé, \[\int \sqrt{x^2-1}= \begin{cases} \frac{1}{2}\mathrm{argcosh }(-x)+\frac{1}{2}x\sqrt{x^2-1} +C_1 & \text{ si } x\leqslant -1\\ \\ -\frac{1}{2}\mathrm{argcosh }(x)+\frac{1}{2}x\sqrt{x^2-1} +C_2 & \text{ si } x\geqslant 1. \end{cases}\] Attention: les constantes \(C_1\) et \(C_2\) peuvent être différentes.

Plus généralement, si la fonction à intégrer contient \[\sqrt{b^2x^2-a^2},\] \(a,b\in \mathbb{R}\) constantes, l'intégrande est définie sur \(\left]-\infty,-\left|\frac{a}{b}\right|\right]\cup \left[\left|\frac{a}{b}\right|,+\infty\right[\). On peut essayer un changement de variable de la forme \[x=\pm\left|\frac{a}{b}\right|\cosh(t),\] en choisissant le signe selon les cas \(x\geqslant \left|\frac{a}{b}\right|\) ou \(x\leqslant -\left|\frac{a}{b}\right|\). Ce changement donnerait \[\sqrt{b^2 x^2-a^2}=\sqrt{b^2\left(\frac{a}{b}\cosh(t)\right)^2-a^2}=\sqrt{a^2(\cosh^2(t)-1)}=|a|\cdot\sinh(t).\]

Dernière compilation: 2024-06-03 (22:36:08)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)