7.12 Longueurs d'arcs

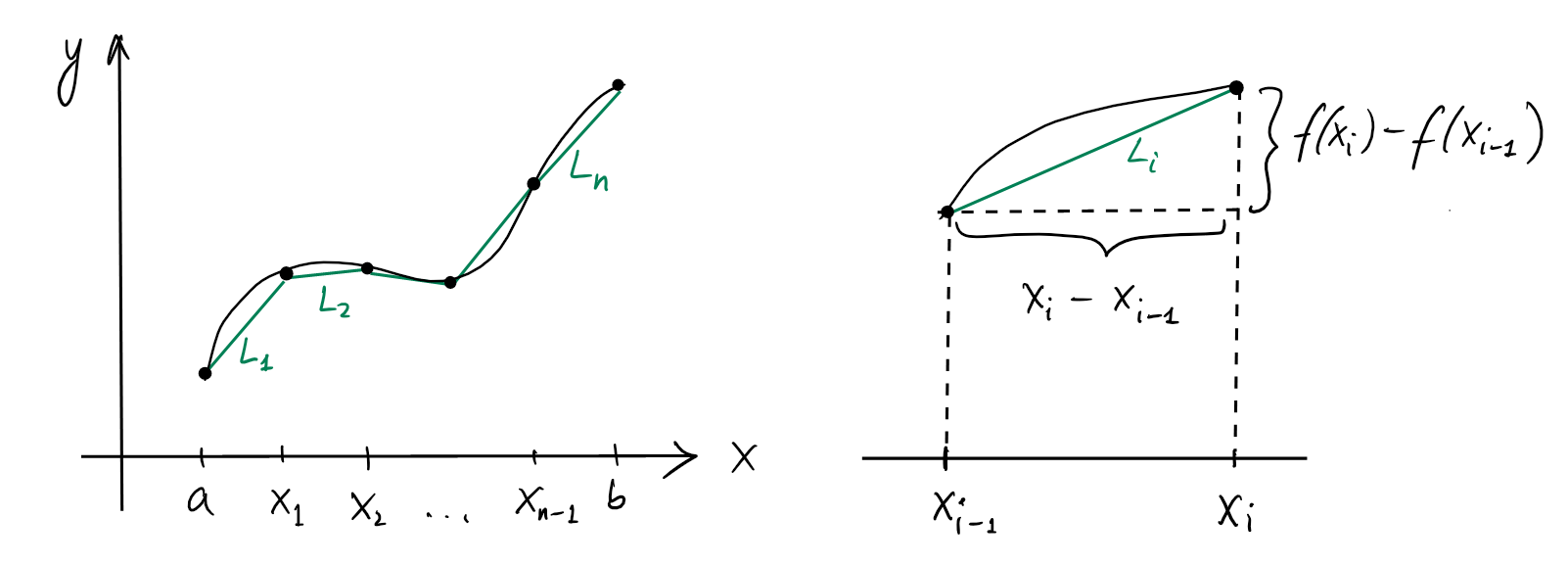
Dans cette section, on voit quelques méthodes pour calculer la longueur d'une courbe dans le plan; on parlera aussi de longueur d'arc.

Longueur du graphe d'une fonction

Considérons pour commencer une fonction \(f:[a,b]\to \mathbb{R}\), et voyons comment calculer la longueur de son graphe, que nous noterons \(L\).

Soit \(\{x_0,x_1, x_2, \ldots, x_n\}\) une subdivision de l'intervalle \([a,b]\). Considérons l'approximation du graphe de \(f\) par la ligne polygonale obtenue en reliant, pour chaque \(i=1,2,\dots,n\), le point \((x_{i-1},f(x_{i-1}))\) à \((x_i,f(x_i))\), par un segment. Soit \(L_i\) la longueur de ce segment.

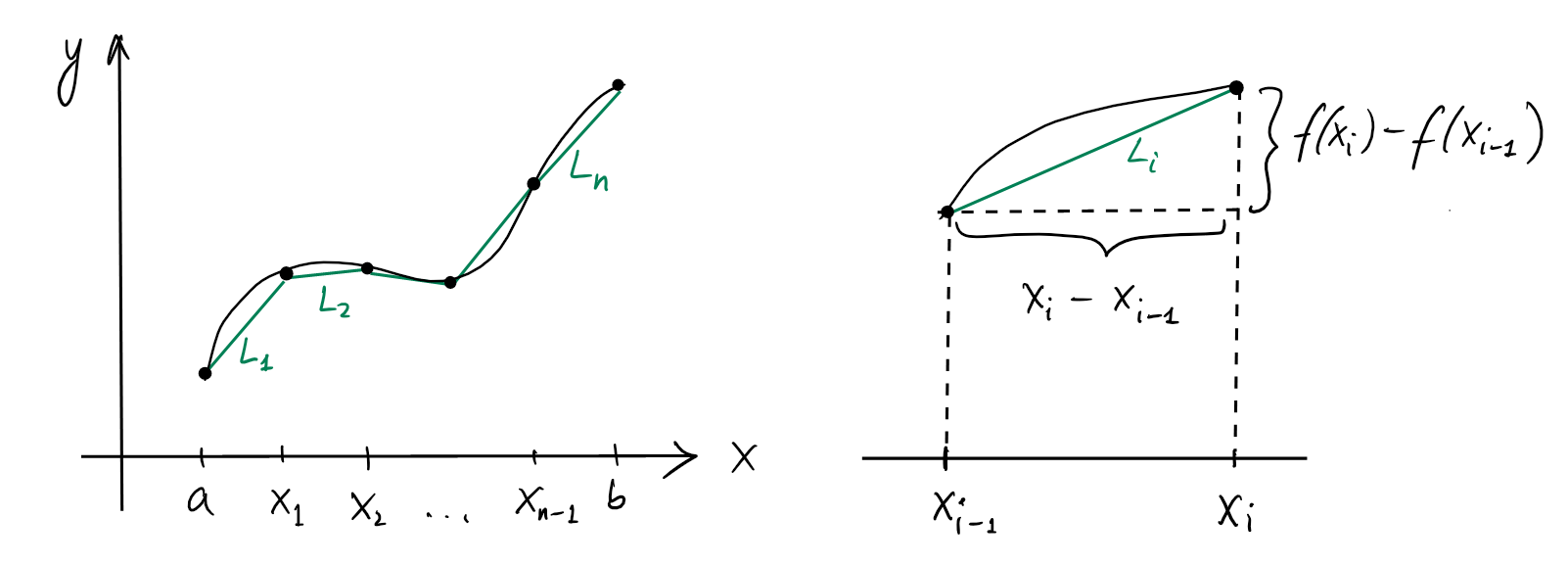
Ainsi, la longueur d'arc \(L\) est approximée par \[ L\simeq \sum_{i=1}^n L_i\,. \] Mais, par le Théorème de Pythagore, on a \[\begin{aligned} L_i &= \sqrt{(x_i-x_{i-1})^2+(f(x_i)-f(x_{i-1}))^2}\\ &=\sqrt{1+\Bigl( \frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}} \Bigr)^2} \cdot(x_i-x_{i-1})\,, \end{aligned}\] et remarquons que si \(f\) est dérivable, alors lorsque \(n\) est grand, \[ \frac{f(x_i)-f(x_{i-1})}{x_i-x_{i-1}}\simeq f'(x_i)\,. \] L'approximation par la ligne polygonale est donc \[ L\simeq \sum_{i=1}^n \sqrt{1+(f'(x_i))^2}\cdot (x_i-x_{i-1})\,. \] Si \(f'\) est elle-même continue, alors dans la limite \(n\to \infty\), cette dernière somme tend vers l'intégrale \[L=\int_a^b \sqrt{1+f'(x)^2} \, dx\]

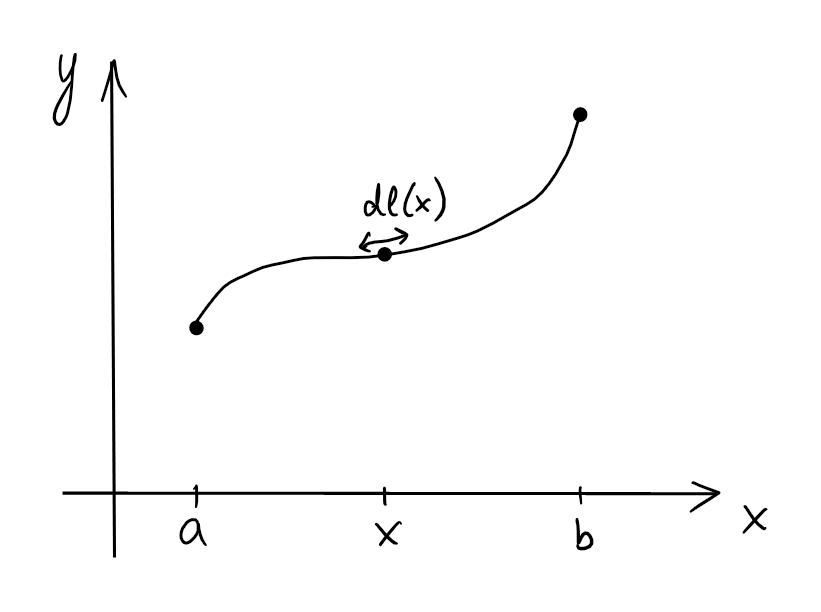
On peut interpréter cette intégrale comme étant \[L=\int_a^b d\ell(x)=\int_a^b \sqrt{1+f'(x)^2} \ dx,\] où \(d\ell(x)=\sqrt{1+f'(x)^2} \ dx\) est l'élément de longueur infinitésimal de la courbe au-dessus du point \(x\):

Exemples:

Longueur d'une courbe paramétrée

Soit maintenant une courbe paramétrée, \[\begin{aligned} M:[\alpha,\beta]&\to \mathbb{R}^2\\ t&\mapsto M(t)=(x(t),y(t)) \end{aligned}\] telle que les fonctions \(x(t)\) et \(y(t)\) sont dérivables et dont les dérivées sont continues. Comme on a fait plus haut, on prend une subdivision régulière \(\{t_0, t_1, \ldots t_n\}\) de l'intervalle \([\alpha, \beta]\) et on approxime la courbe en prenant sur chaque intervalle \([t_{i-1},t_i]\) le segment de droite reliant \(M(t_{i-1})\) à \(M(t_i)\). Soit \(L_i\) la longueur de ce segment.

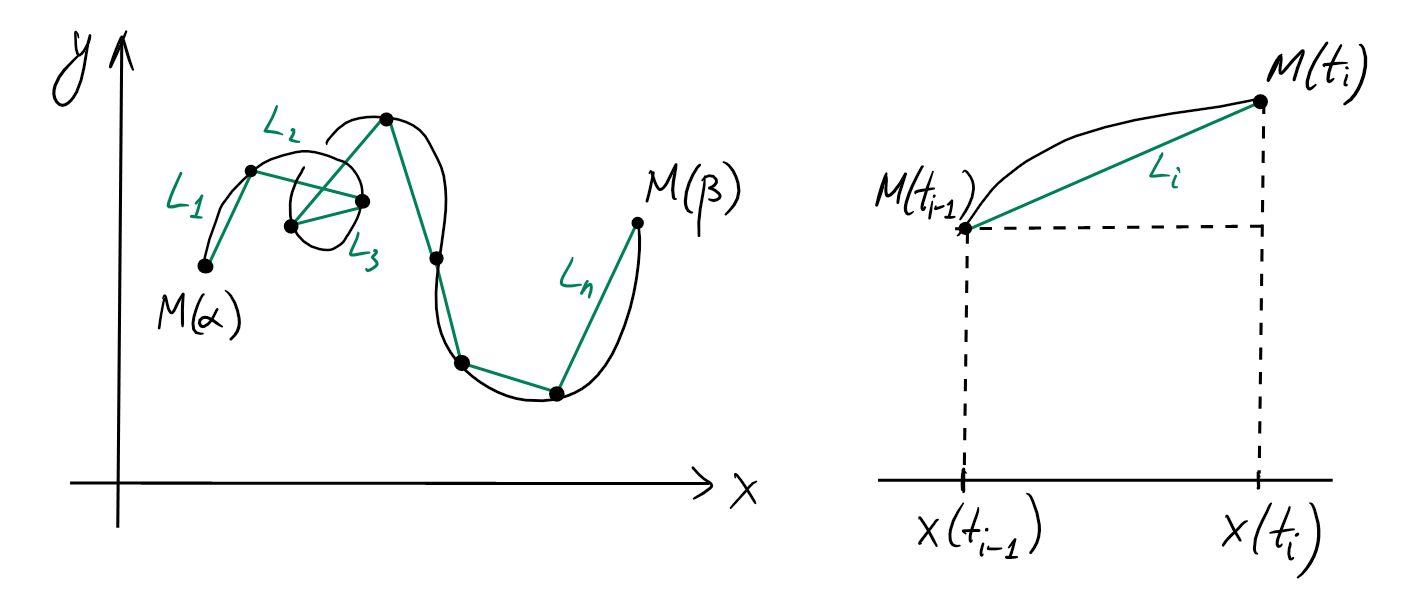
Ainsi, la longueur d'arc \(L\) est approximée par \[L\simeq \sum_{i=1}^n L_i\,.\] Par le Théorème de Pythagore, \[\begin{aligned} L_i &= \sqrt{(x(t_i)-x(t_{i-1}))^2+(y(t_i)-y(t_{i-1}))^2}\\ &=\sqrt{ \Bigl( \frac{x(t_i)-x(t_{i-1})}{t_i-t_{i-1}} \Bigr)^2 +\Bigl( \frac{y(t_i)-y(t_{i-1})}{t_i-t_{i-1}} \Bigr)^2 } \cdot (t_i-t_{i-1}). \end{aligned}\] Encore une fois, si \(x(t)\) et \(y(t)\) sont dérivables alors lorsque \(n\) est grand, \[ \frac{x(t_i)-x(t_{i-1})}{t_i-t_{i-1}} \simeq \dot{x}(t_i) \,,\qquad \frac{y(t_i)-y(t_{i-1})}{t_i-t_{i-1}} \simeq \dot{y}(t_i)\,, \] et l'approximation par la ligne polygonale est \[ L \simeq \sum_{i=1}^n \sqrt{\dot{x}(t_i)^2+\dot{y}(t_i)^2}\cdot (t_i-t_{i-1}) \] Lorsque les dérivées \(\dot{x}(t)\) et \(\dot{y}(t)\) sont continues, cette dernière somme converge, lorsque \(n\to \infty\), vers l'intégrale \[L=\int_{\alpha}^{\beta} \sqrt{\dot{x}(t)^2+\dot{y}(t)^2} \ dt\] On remarque qu'en prenant le vecteur tangent \[\dot{\vec{r}}(t)= \begin{pmatrix} \dot{x}(t)\\ \dot{y}(t) \end{pmatrix},\] la formule ci-dessus devient \[L=\int_{\alpha}^{\beta} \|\dot{\vec{r}}(t)\| \ dt.\]

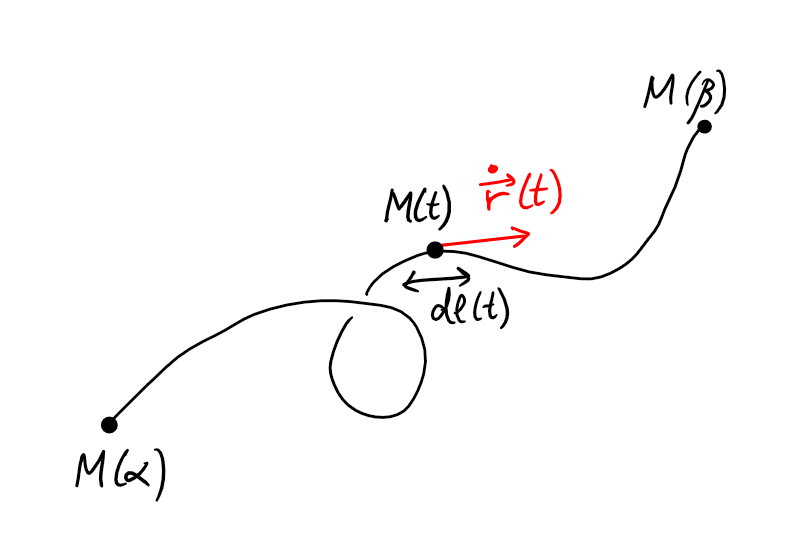
On a \[L=\int_{\alpha}^{\beta} d\ell(t)=L=\int_{\alpha}^{\beta} \|\dot{\vec{r}}(t)\| \ dt,\] où \(d\ell(t)=\|\dot{\vec{r}}(t)\| \ dt\) est l'élément de longueur infinitésimal.

Exemple: Calculons la circonférence d'un cercle de rayon \(R\) (que l'on sait être égale à \(2\pi R\)), que l'on peut centrer à l'origine.

Utilisons la paramétrisation \(t\mapsto M(t)=(R\cos(t),R\sin(t))\), \(t\in[0,2\pi]\). On a \[ \dot{\vec{r}}(t)= \begin{pmatrix} -R\sin(t)\\ R\cos(t) \end{pmatrix}\,, \] et donc \[\begin{aligned} L&=\int_0^{2\pi}\|\dot{\vec{r}}(t)\| \ dt\\ &=\int_0^{2\pi}\sqrt{(-R\sin(t))^2+(R\cos(t))^2} \ dt\\ &= \int_0^{2\pi} R \ dt\\ &=2\pi R. \end{aligned}\]

Exemple: Une cycloïde est la trajectoire décrite par un point \(M\) fixé sur le bord d'un disque de rayon \(R\), lorsque ce dernier roule sur la droite:

On se propose ici de calculer la longueur de la cycloïde, lorsque le disque effectue un tour complet.

Pour paramétriser la position du point \(M(t)=(x(t),y(t))\), utilisons l'angle \(t\in[0,2\pi]\) fait par le rayon (segment reliant le centre du disque au point) avec la verticale. La position du centre du disque pour une valeur \(t\) de l'angle est donnée par \[C(t)=(Rt,R)\] Ensuite, \[\overrightarrow{C(t) M(t)}=\begin{pmatrix} -R\sin(t)\\ -R\cos(t) \end{pmatrix}\] Donc, par la relation de Chasles, \[ \overrightarrow{OM(t)} = \overrightarrow{OC(t)} + \overrightarrow{C(t) M(t)}\,, \] et donc \[ \overrightarrow{OM(t)} = \begin{pmatrix} Rt-R\sin(t)\\ R-R\cos(t) \end{pmatrix}\,, \quad t\in [0,2\pi] \] La longueur d'arc est donc donnée par \[\begin{aligned} L&= \int_0^{2\pi} \sqrt{\dot{x}(t)^2+\dot{y}(t)^2} \ dt\\ &= \int_0^{2\pi} \sqrt{(R-R\cos(t))^2+(R\sin(t))^2} \ dt\\ &= R \int_0^{2\pi} \sqrt{2-2\cos(t)} \ dt\\ &= \sqrt{2}R \int_0^{2\pi} \sqrt{1-\cos(t)} \ dt\\ &= \sqrt{2}R \int_0^{2\pi} \sqrt{2\sin^2\bigl(\tfrac{t}{2}\bigr)} \, dt \quad (u=\tfrac{t}{2})\\ &= \sqrt{2}^2 R \int_0^{\pi} |\sin(u)| \cdot 2 \, du\\ &=4 R \int_0^{\pi} \sin(u) \ du\\ &=8R. \end{aligned}\]

Dernière compilation: 2024-06-03 (22:36:08)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)