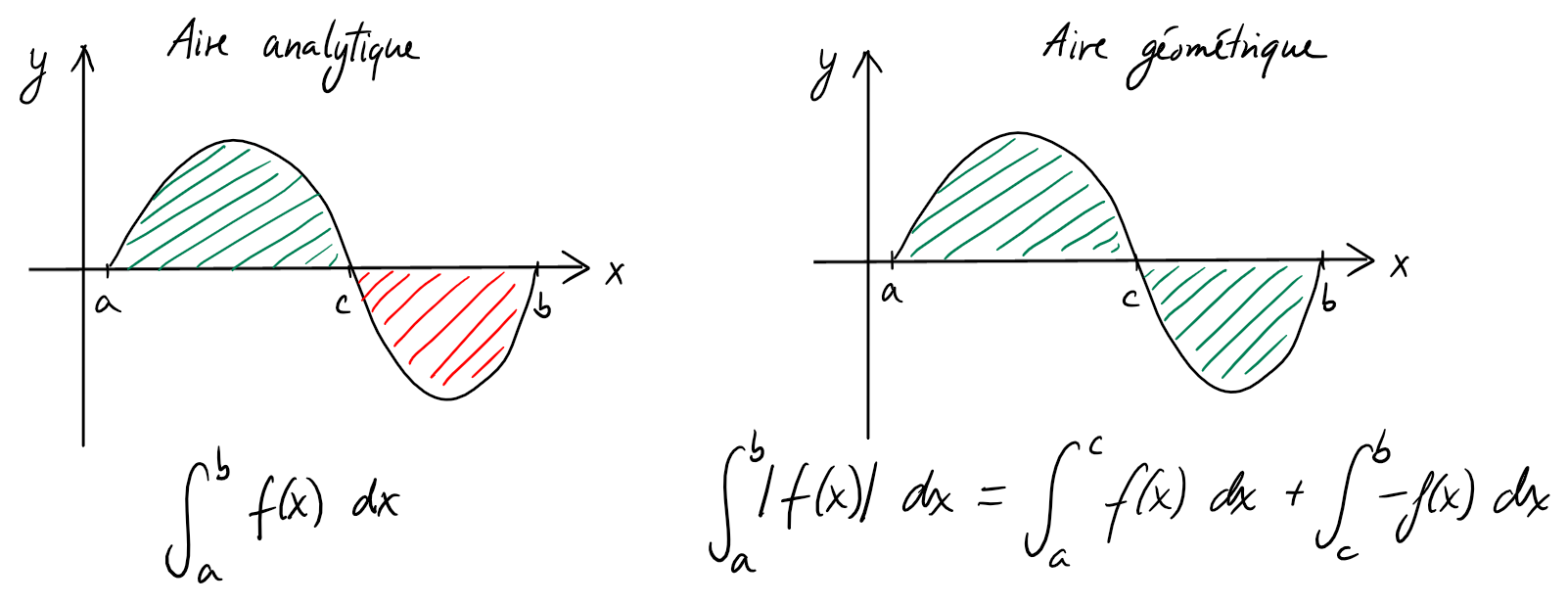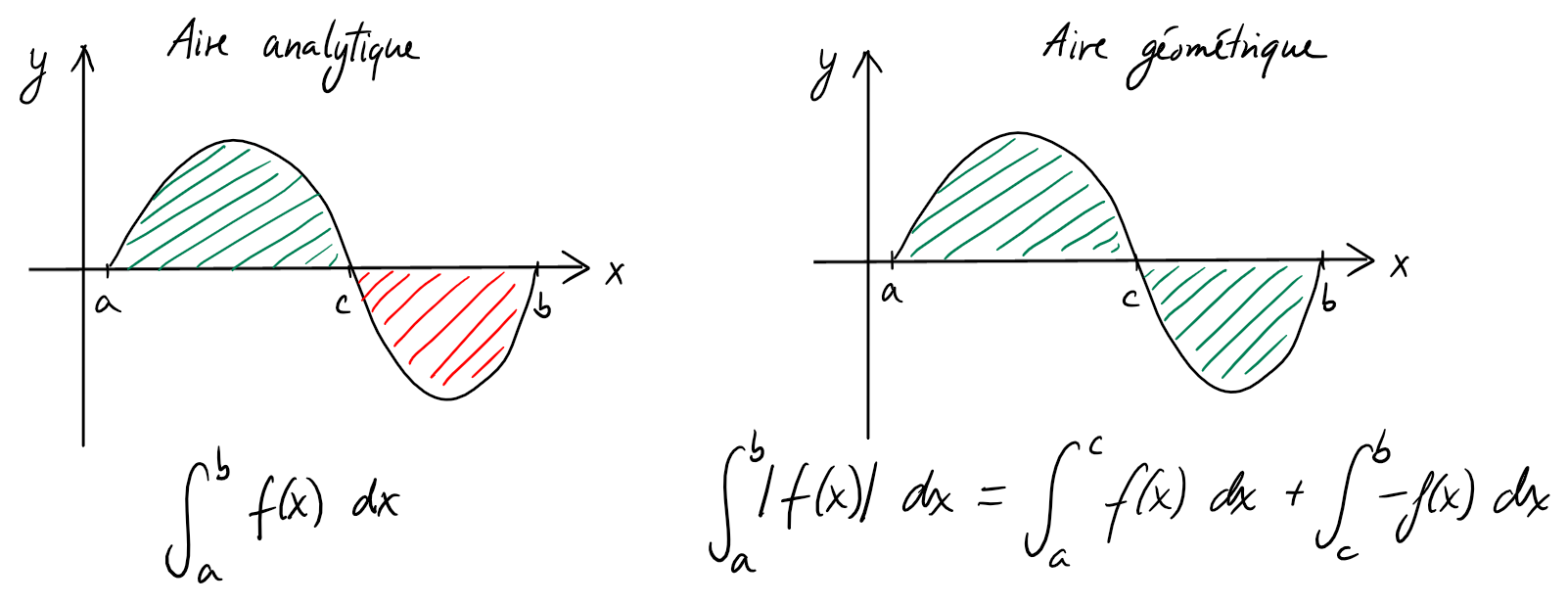7.10 Aires de régions du plan

On a vu que l'aire analytique définie par le graphe d'une fonction \(f\) et l'axe \(Ox\) est donnée par \(\int_a^b f(x) \ dx\).

L'aire géométrique est donnée par \(\int_a^b |f(x)| \ dx\).

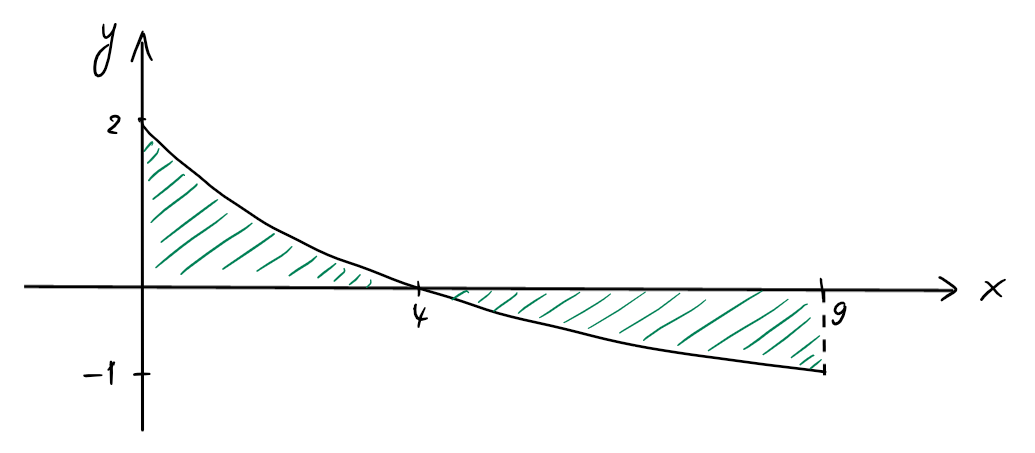
Exemple: Calculons l'aire géométrique \(A\) de la région du plan délimitée par la courbe \(y=f(x)=2-\sqrt{x}\), les axes \(Ox\) et \(Oy\) et la droite \(x=9\).

Remarquons que \(f\) change de signe en \(x=4\). Donc \[\begin{aligned} A &= \int_0^9 |f(x)| \ dx\\ &= \int_0^4 f(x) \ dx + \int_4^9 [-f(x)] \ dx\\ &= \int_0^4 [2-\sqrt{x}] \ dx + \int_4^9 [-2+\sqrt{x}] \ dx\\ &= \left.\left[2x-\frac{2}{3} x^{\frac{3}{2}}\right]\right\vert_0^4+\left.\left[-2x+\frac{2}{3} x^{\frac{3}{2}}\right]\right\vert_4^9\\ &=\left(8-\frac{2}{3}\cdot 8\right)-0+\left(-2\cdot 9 +\frac{2}{3}\cdot 27\right)-\left(-8+\frac{2}{3}\cdot 8\right)\\ &=\frac{16}{3}. \end{aligned}\]

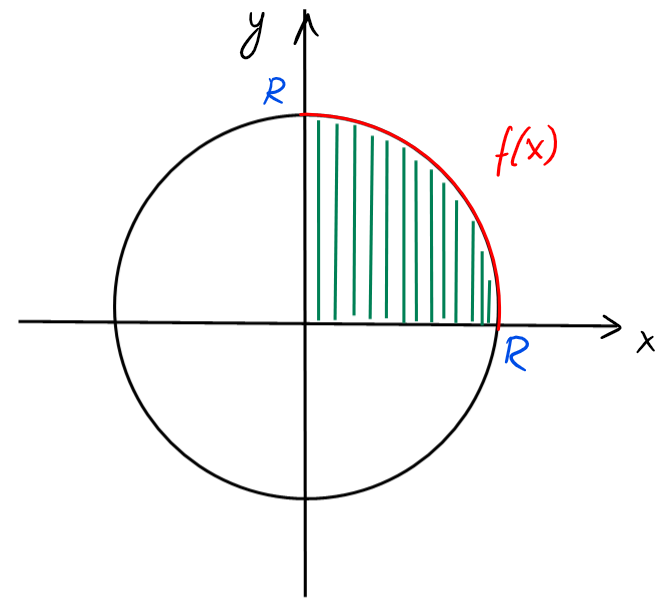
Exemple: Calculons l'aire \(A\) du disque de rayon \(R\) centré à l'origine.

L'équation du cercle est \(x^2+y^2=R^2\), et pour \(x,y\geqslant 0\), on a \[y=\sqrt{R^2-x^2}=:f(x).\] On a donc \[ A = 4\int_0^R f(x) \ dx = 4\int_0^R \sqrt{R^2-x^2} \ dx\,. \] En posant \(x=\varphi(t):=R\sin(t)\), cette dernière devient \[\begin{aligned} 4\int_0^{\frac{\pi}{2}}\sqrt{R^2-(R\sin(t))^2} \cdot \underbrace{R\cos(t)}_{\varphi'(t)} \ dt &= 4R^2 \int_0^{\frac{\pi}{2}} \cos^2(t) \ dt\\ &= 4R^2 \left.\left[\frac{1}{2} t +\frac{1}{4}\sin(2t)\right]\right\vert_0^{\frac{\pi}{2}}\\ &= 4R^2 \frac{\pi}{4}\\ &=\pi R^2. \end{aligned}\]

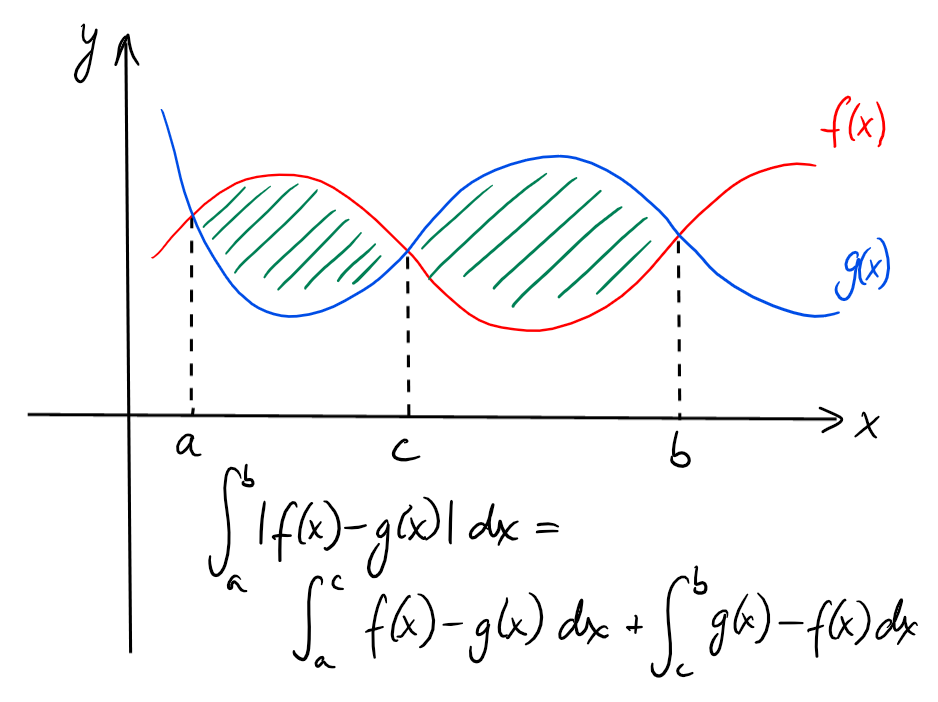
On peut aussi calculer l'aire entre deux courbes \(y=f(x)\) et \(y=g(x)\). Pour ceci, il est utile de

• trouver les points d'intersection des courbes,
• esquisser le domaine,
• calculer l'aire \(A=\int_a^b |f(x)-g(x)| \ dx\).

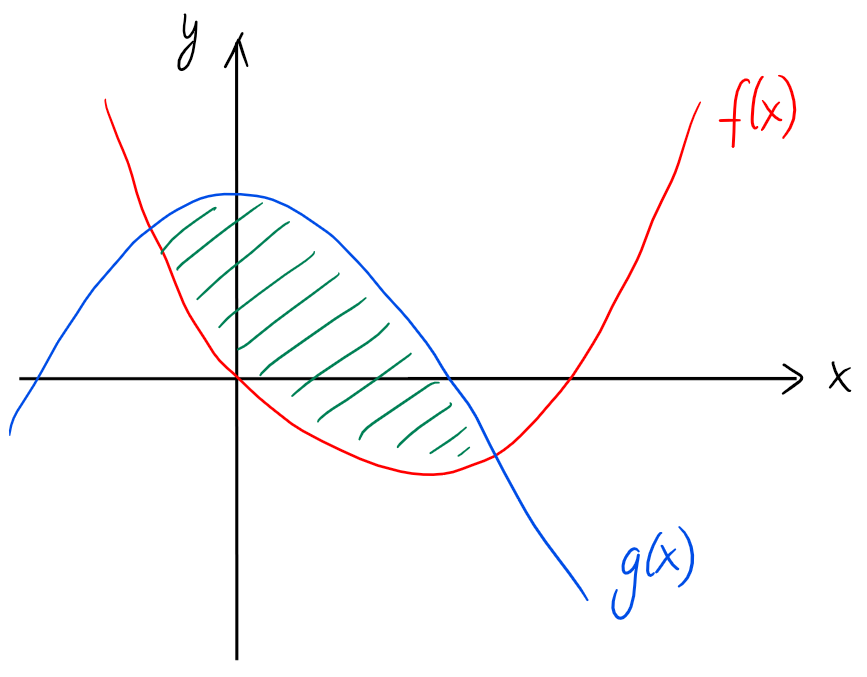
Exemple: Calculons l'aire \(A\) de la région bornée, délimitée par les courbes \[y=x^2-4x=:f(x), \quad y=6-x^2=:g(x).\] Un simple croquis permet de comprendre la situation:

Commençons par chercher les points d'intersection des deux graphes: \[\begin{aligned} f(x)=g(x) &\iff x^2-4x=6-x^2\\ &\iff 2x^2-4x-6=0\\ &\iff (2x+2)(x-3)=0\\ &\iff x=-1 \text{ ou } x=3. \end{aligned}\] Comme le graphe de \(g\) est au-dessus de celui de \(f\) sur \([-1,3]\), on a \(|f(x)-g(x)|=g(x)-f(x)\) sur cet intervalle, et donc l'aire cherchée vaut \[\begin{aligned} A &= \int_{-1}^3 |f(x)-g(x)| \ dx\\ &= \int_{-1}^3 g(x)-f(x) \ dx\\ &= \int_{-1}^3 (6-x^2)-(x^2-4x) \ dx\\ &= \int_{-1}^3 -2x^2+4x+6 \ dx\\ &= \left.\left(\frac{-2}{3}x^3+\frac{4}{2}x^2+6x\right)\right\vert_{-1}^3\\ &= \frac{64}{3}. \end{aligned}\]

L'aire d'une région peut en souvent s'exprimer aussi à l'aide d'une intégration selon \(y\), ce qiu peut parfois simplifier les calculs.

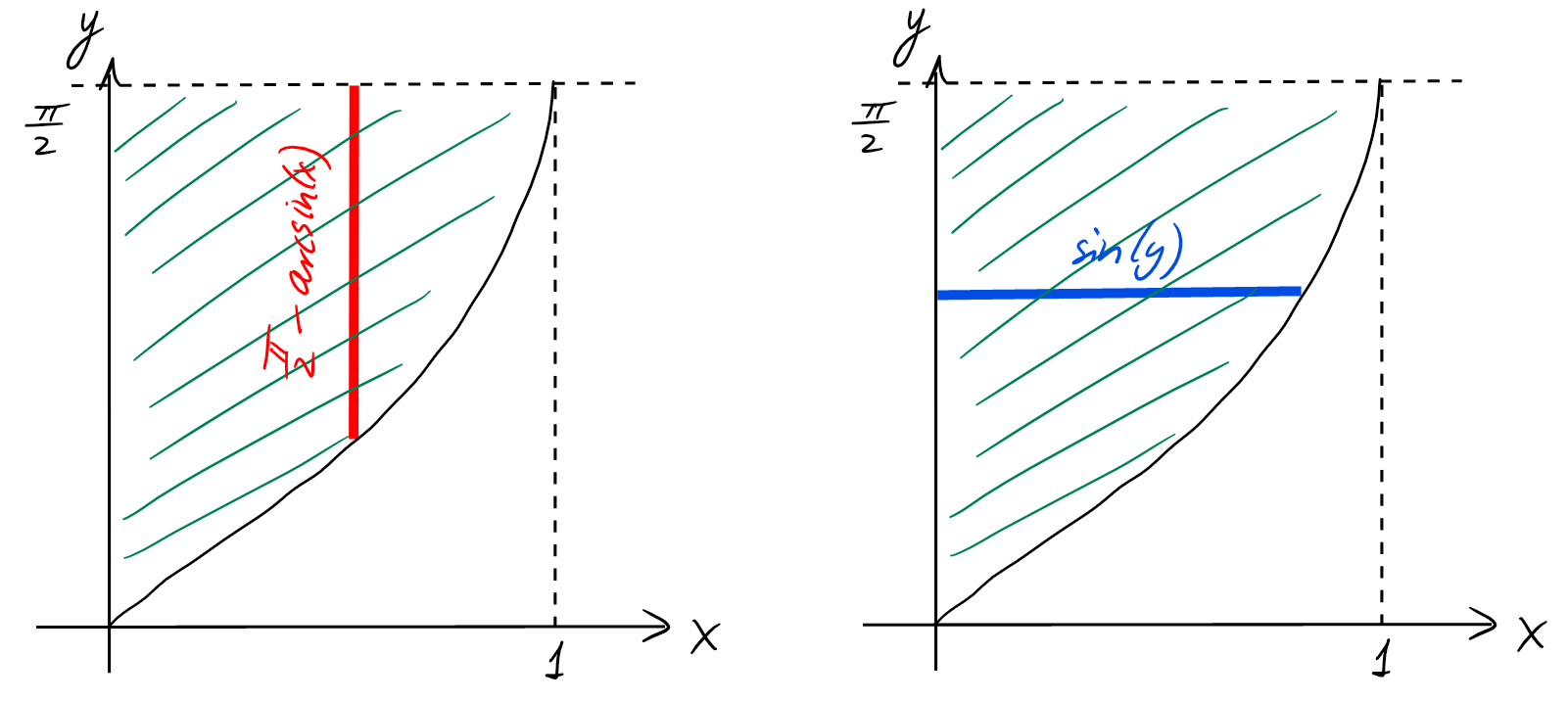
Exemple: Calculons l'aire \(A\) de la région délimitée par l'axe \(Oy\), la droite \(y=\frac{\pi}{2}\) et la courbe \(y=f(x)=\arcsin(x)\).

Commençons à intégrer par rapport à \(x\): \[ A = \int_0^1 \left(\tfrac{\pi}{2}-\arcsin(x)\right) \ dx =\frac{\pi}{2}-\int_0^1 \arcsin(x) \ dx \] En posant \(x=\sin(t)\), \[\begin{aligned} A &= \frac{\pi}{2} - \int_0^{\frac{\pi}{2}} \arcsin(\sin(t)) \cos(t) \ dt \\ &= \frac{\pi}{2} - \int_0^{\frac{\pi}{2}} t\cos(t) \ dt \\ &= \frac{\pi}{2} - \left[\left.t\sin(t)\right\vert_0^{\frac{\pi}{2}} -\int_0^{\frac{\pi}{2}} \sin(t) \ dt \right] \\ &= \frac{\pi}{2} -\frac{\pi}{2}-\left.\cos(t)\right\vert_0^{\frac{\pi}{2}}\\ &= 1. \end{aligned}\] Regardons maintenant ce qui se passe en intégrant par rapport à \(y\): \[\begin{aligned} A &= \int_0^{\frac{\pi}{2}} \sin(y) \ dy\\ &= -\cos(x)\bigr\vert_0^{\frac{\pi}{2}}\\ &= 1. \end{aligned}\]

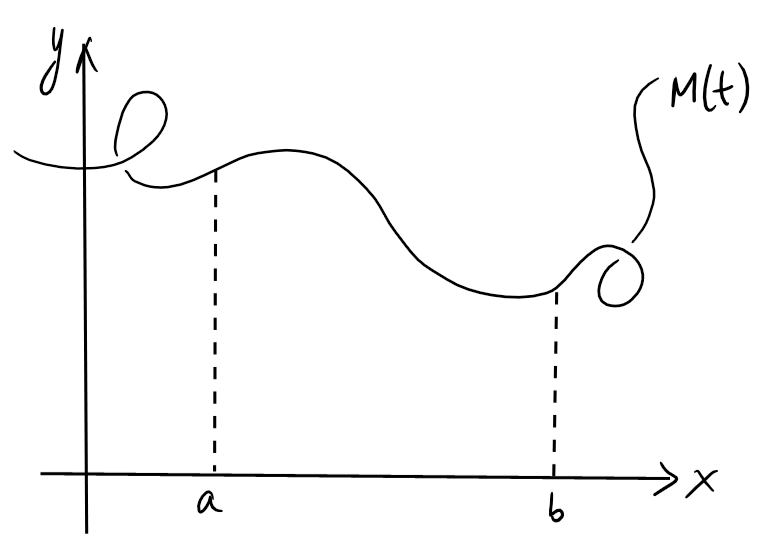
Régions délimitées par des courbes paramétrées

Soit maintenant \[\begin{aligned} M:[\alpha,\beta]&\to \mathbb{R}^2\\ t&\mapsto M(t)=(x(t),y(t)) \end{aligned}\] une courbe paramétrée. Pour simplifier, supposons que la portion de courbe pour \(t\in [\alpha,\beta]\) est située au-dessus de l'axe \(Ox\), et qu'elle ne s'auto-intersecte pas:

Comment calcule-t-on l'aire \(A\) sous la courbe, à l'aide d'une intégrale en la variable \(t\)?

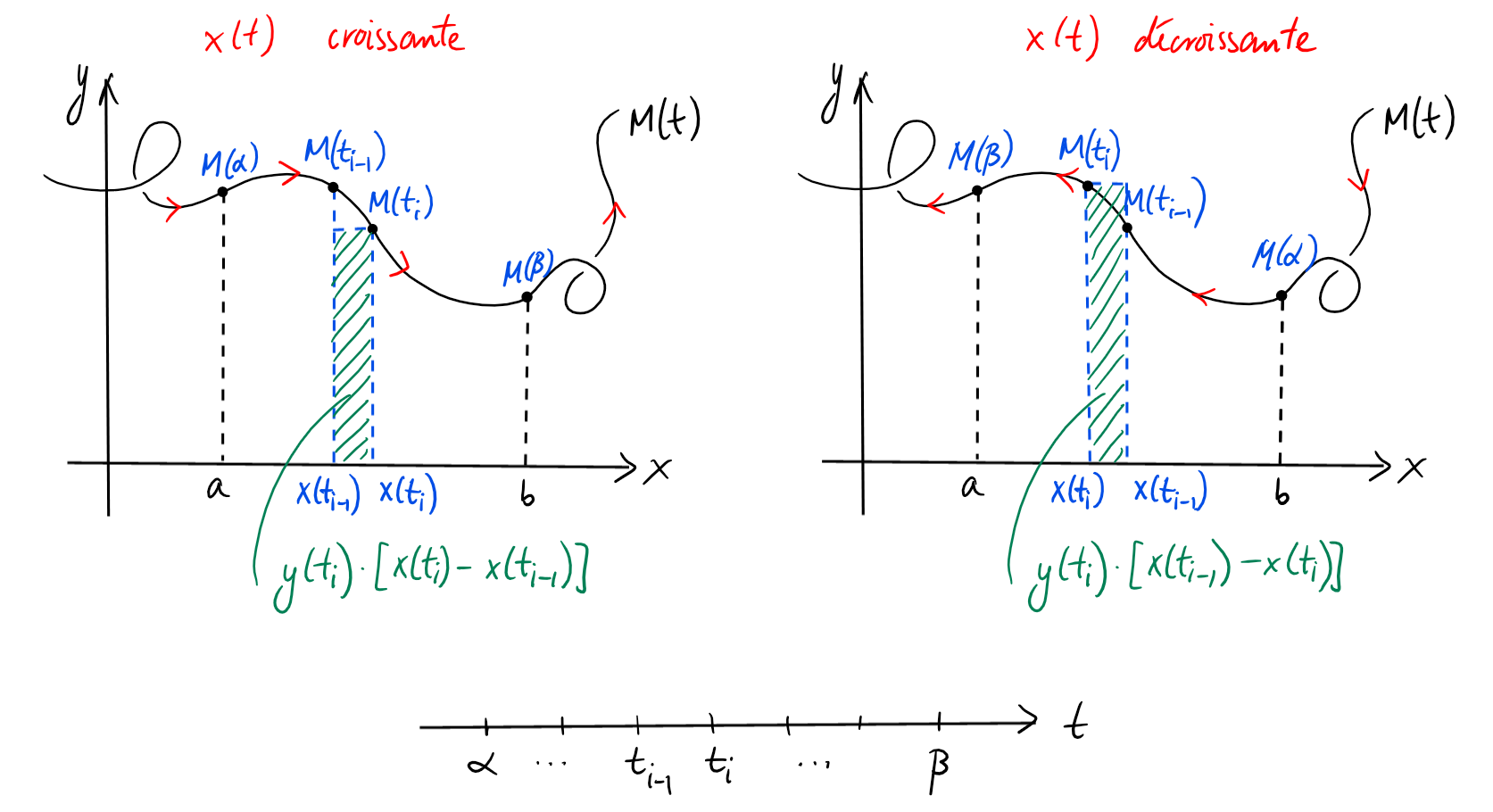
Supposons d'abord que la fonction \(x(t)\) est croissante, c'est-à-dire, que la particule se déplace vers la droite.

En prenant une partition \(\{t_0,t_1,\ldots,t_{n-1},t_n\}\) suffisamment fine de l'intervalle du temps \([\alpha,\beta]\), on a \[\begin{aligned} A &\simeq \sum_{i=1}^n y(t_i)\cdot [\underbrace{x(t_i)-x(t_{i-1})}_{\geqslant 0}]\\ &= \sum_{i=1}^n y(t_i) \cdot \underbrace{\frac{x(t_i)-x(t_{i-1})}{t_i-t_{i-1}}}_{\simeq \dot{x}(t_i)}\cdot (t_i-t_{i-1}), \end{aligned}\] et si \(x(t)\) est une fonction dérivable avec dérivée continue, on peut montrer que lorsque \(n\to \infty\), \[A=\int_\alpha^\beta y(t)\cdot \dot{x}(t) \ dt.\]

Si la fonction \(x(t)\) est décroissante, c'est-à-dire, la particule se déplace vers la gauche, alors on a \[\begin{aligned} A &\simeq \sum_{i=1}^n y(t_i)\cdot [\underbrace{x(t_{i-1})-x(t_i)}_{\geqslant 0}]\\ &= \sum_{i=1}^n y(t_i) \cdot \underbrace{\frac{-[x(t_i)-x(t_{i-1})]}{t_i-t_{i-1}}}_{\simeq -\dot{x}(t_i)}\cdot (t_i-t_{i-1}), \end{aligned}\] et si \(x(t)\) est une fonction dérivable avec dérivée continue, on peut montrer que lorsque \(n\to \infty\), \[A=\int_\alpha^\beta y(t)\cdot(-\dot{x}(t)) \ dt.\]

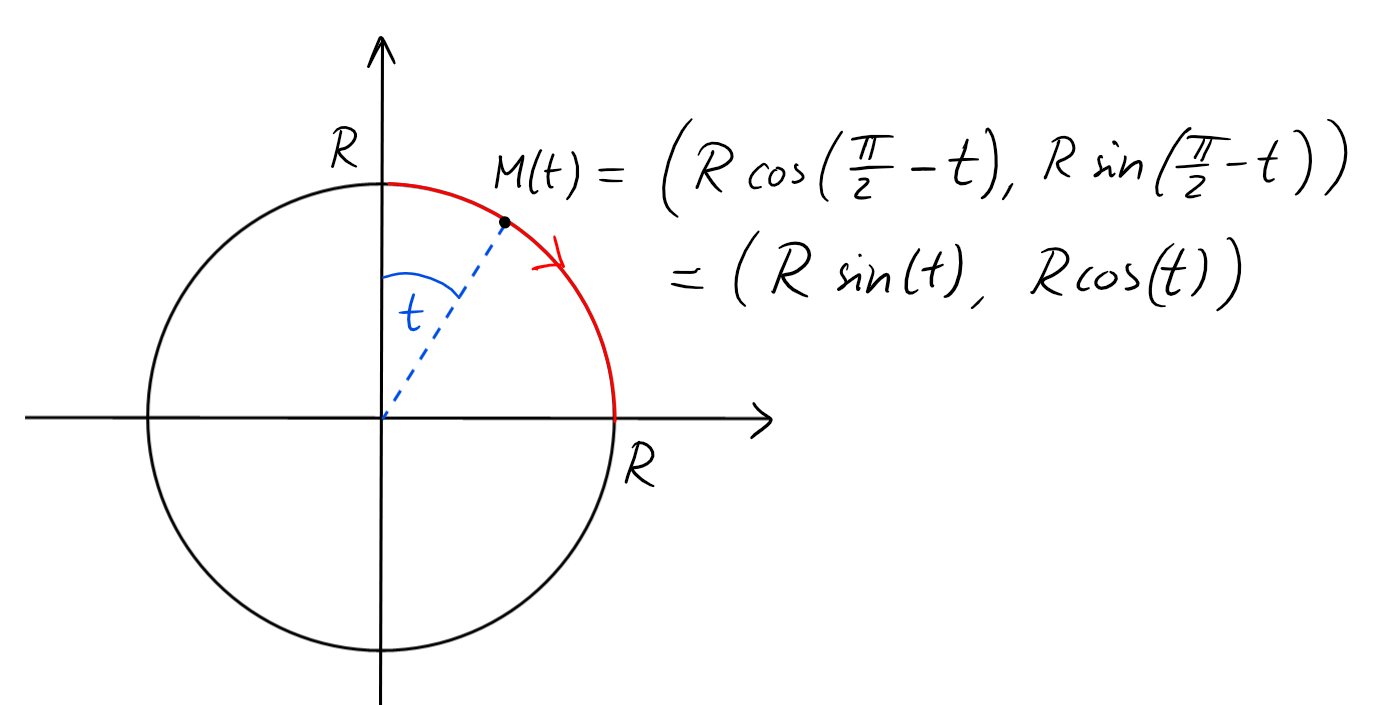
Exemple: Calculons l'aire \(A\) du disque de rayon \(R\).

Paramétrisons le quart de cercle \(x,y\geqslant 0\) ainsi: \[\begin{aligned} M:[0,\pi/2]&\to \mathbb{R}^2\\ t&\mapsto M(t)=(R\sin(t),R\cos(t)). \end{aligned}\] La fonction \(x(t)\) est croissante sur \([0,\pi/2]\) et donc \[A=4\int_0^{\pi/2} \underbrace{R\cos(t)}_{=y(t)} \cdot \underbrace{R\cos(t)}_{=\dot{x}(t)} \ dt= 4R^2\int_0^{\pi/2}\cos^2(t) \ dt =\pi R^2.\]

---

Dernière compilation: 2024-06-03 (22:36:08)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)