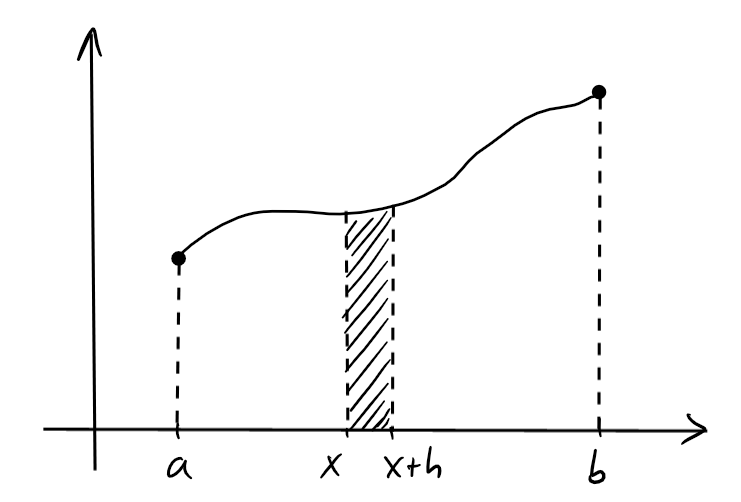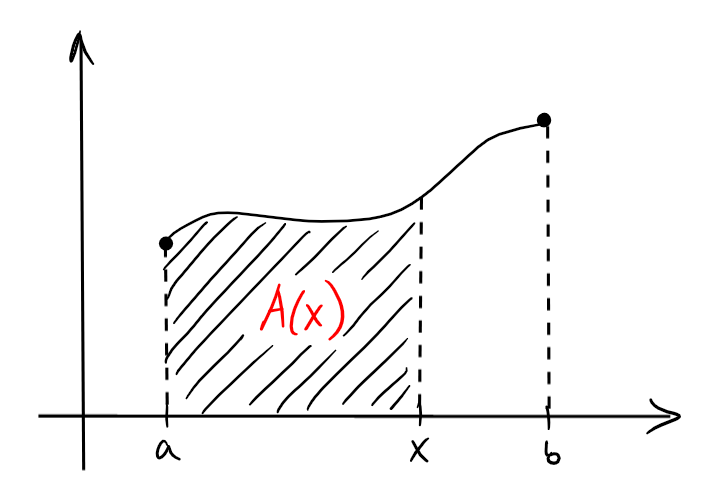

On remarque que
Voyons deux exemples où la fonction aire se calcule facilement:
Exemples:
On a vu dans ces deux exemples que la fonction aire était dérivable et que de plus \(A'(x)=f(x)\). Cette propriété est vraie en général:
Théorème: (Théorème Fondamental de l'Analyse, 1ère partie) Soit \(f:[a,b]\to \mathbb{R}\) continue, et soit \(A:[a,b]\to \mathbb{R}\) la fonction aire associée. Alors \(A(x)\) est dérivable sur \(]a,b[\) et \[A'(x)=f(x) \quad \forall x\in ]a,b[.\]
On doit montrer que pour tout \(x\in ]a,b[\), \[ \lim_{h\to 0} \frac{A(x+h)-A(x)}{h}=f(x)\,. \] Soit donc \(x\in ]a,b[\), et soit \(h\gt 0\).