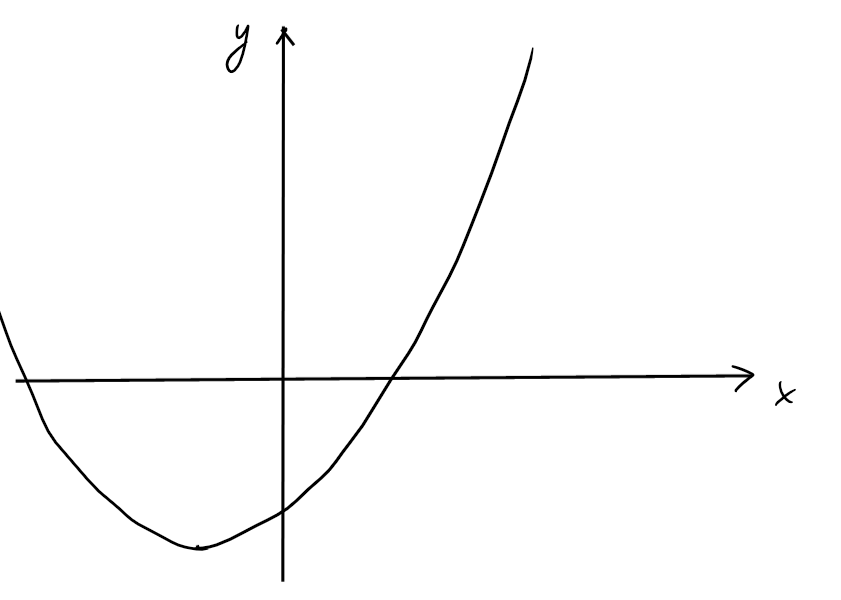Analyse B (MAN)

Parlons d'abord de la surjectivité. La condition \(\mathrm{Im} (f)=B\) veut dire que pour chaque élément \(b\in B\), il y a un élément de \(a\) qui est envoyé sur \(b\) par \(f\): \(f(a)=b\).

Si une fonction \(f:A\rightarrow B\) n'est pas surjective, on peut toujours restreindre son ensemble d'arrivée pour qu'elle le devienne.

Exemple: Soit \[\begin{aligned} f\colon &\mathbb{R} \rightarrow \mathbb{R}\\ &x \mapsto x^2-4x \end{aligned}\] On a vu dans un exemple précédent que \(\mathrm{Im} (f)=[-4,\infty[\). La fonction \(f\) n'est donc pas surjective, puisque \([-4,\infty[\neq \mathbb{R}\). Par contre, la fonction \[\begin{aligned} \tilde{f}\colon &\mathbb{R} \rightarrow [-4,\infty[\\ &x \mapsto x^2-4x \end{aligned}\] est surjective.

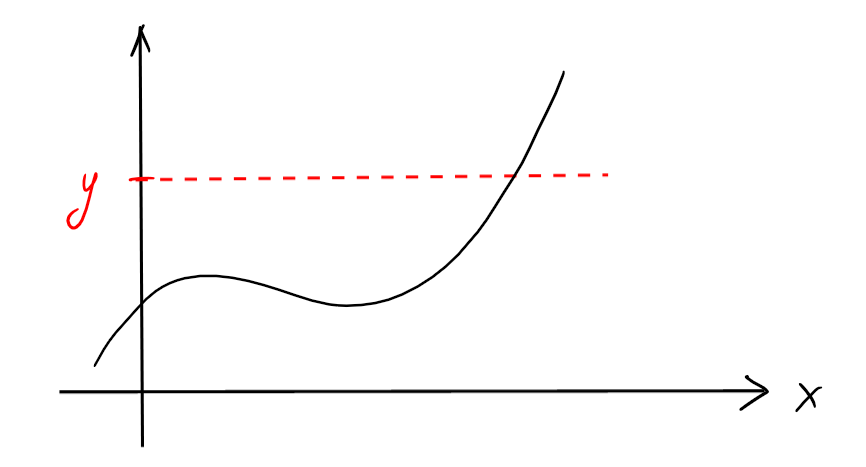
Graphiquement, une fonction réelle est surjective si pour tout \(y\in \mathbb{R}\), la droite horizontale à hauteur \(y\) coupe le graphe de \(f\) en au moins un point.

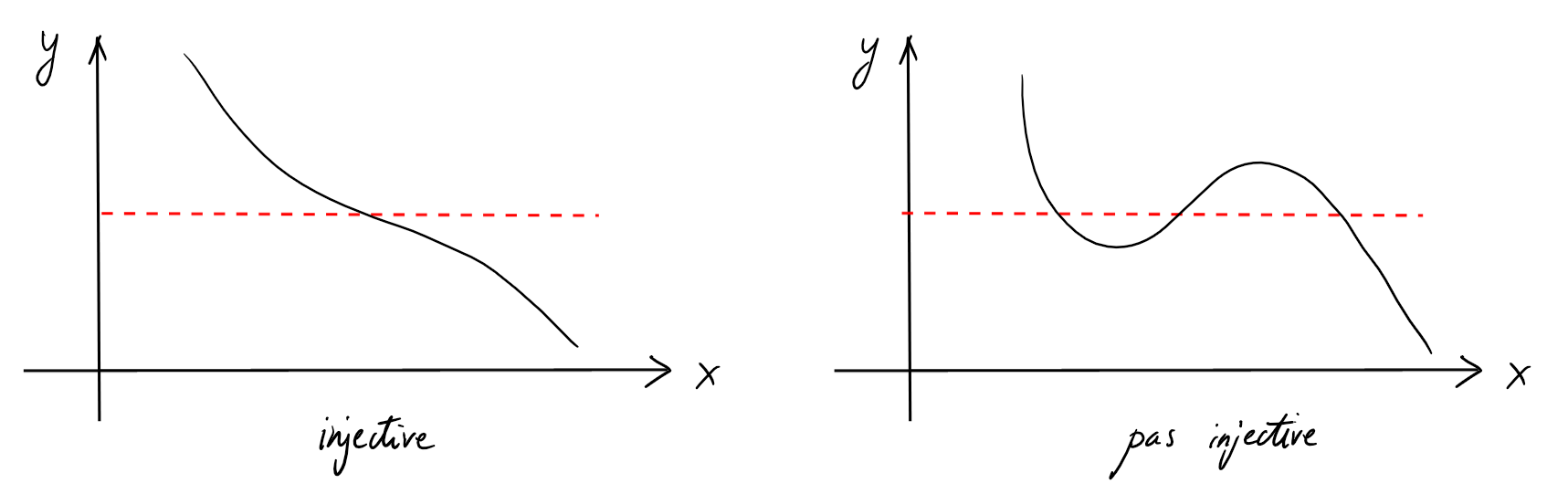
Ensuite, l'injectivité peut être décrite graphiquement ainsi: \(f\) est injective si pour tout \(y\in \mathbb{R}\), la droite horizontale à hauteur \(y\) coupe le graphe de \(f\) en au plus un point.

Une fonction \(f\) est injective si et seulement si \[ \forall x, x'\in D_f, \, x\neq x' \Longrightarrow f(x)\neq f(x')\,. \] Ceci veut dire que deux éléments distincts ne peuvent pas avoir la même image par \(f\). Cette condition est équivalente à sa contraposée: \[ \forall x, x'\in D_f, \ f(x)=f(x') \Longrightarrow x=x'\,. \]

Exemples:

\(f\colon \mathbb{R} \rightarrow \mathbb{R}, \ x \mapsto x^2\) n'est pas injective, car \(-1\neq 1\) mais \(f(-1)=1=f(1)\). Par contre, \(f\colon \mathbb{R}_+ \rightarrow \mathbb{R}, \ x \mapsto x^2\) est injective.
La fonction \(f\colon \mathbb{R}_+ \rightarrow \mathbb{R}, \ x \mapsto \frac{x}{\sqrt{x^2+1}}\) est-elle injective ? On a \[\begin{aligned} f(x)=f(x') &\iff \frac{x}{\sqrt{x^2+1}}=\frac{x'}{\sqrt{(x')^2+1}}\\ &\Longrightarrow \frac{x^2}{x^2+1}=\frac{(x')^2}{(x')^2+1}\\ &\Longrightarrow x^2((x')^2+1)=(x')^2(x^2+1)\\ &\Longrightarrow x^2=(x')^2\\ &\Longrightarrow x^2-(x')^2=0\\ &\Longrightarrow (x-x')(x+x')=0. \end{aligned}\] Puisque \(\frac{x}{\sqrt{x^2+1}}=\frac{x'}{\sqrt{(x')^2+1}}\) implique que \(\mathrm{sgn}(x)=\mathrm{sgn}(x')\), on a donc \[f(x)=f(x')\Longrightarrow x-x'=0 \Longrightarrow x=x',\] d'où la fonction est injective.
La fonction \(f\colon \mathbb{R}^* \rightarrow \mathbb{R}, \ x \mapsto x-\frac{4}{x}\) est-elle injective ? On a \[\begin{aligned} f(x)=f(x') &\iff x-\frac{4}{x}=x'-\frac{4}{x'}\\ &\iff x^2x'-4x'=x(x')^2-4x\\ &\iff (x-x')(xx'+4)=0\\ &\iff x=x' \text{ ou } x'=\frac{-4}{x}. \end{aligned}\] Si \(x'=\frac{-4}{x}\), on a donc \(f(x)=f(x')\). On peut prendre par exemple \(x=1\) et \(x'=-4\neq x\), et on aura \(f(1)=f(-4)\). La fonction n'est donc pas injective.

On remarque que pour montrer qu'une fonction \(f\) réelle n'est pas injective, il suffit de trouver deux nombres réels distincts qui sont envoyé au même nombre réel.

Preuve:

Soit \(f\) strictement croissante (la preuve est similaire dans le cas d'une fonction strictement décroissante). Soit \(x\neq x'\). Alors on a \(x\lt x'\) (ou \(x'\lt x\)) et donc \(f(x)\lt f(x')\) (respectivement \(f(x')\lt f(x)\)). Ainsi, \(f(x)\neq f(x')\).

On a alors que pour une fonction bijective \(f:A \rightarrow B\), tout \(y\in B\) possède exactement une préimage. Ceci nous permet de définir la fonction \[\begin{aligned} f^{-1}:B&\rightarrow A\\ y\mapsto \text{ l'unique préimage de } y. \end{aligned}\] Cette fonction est appelée la fonction réciproque de \(f\). On a \[\begin{aligned} f(f^{-1}(y))&=y \qquad \forall y\in B,\\ f^{-1}(f(x))&=x \qquad \forall x\in A. \end{aligned}\]

Exemples:

\(f: \mathbb{R}_+ \rightarrow \mathbb{R}_+, \ x\mapsto x^2\) est bijective. Sa réciproque est la racine carrée, \(f^{-1}: \mathbb{R}_+ \rightarrow \mathbb{R}_+, \ y\mapsto \sqrt{y}\).
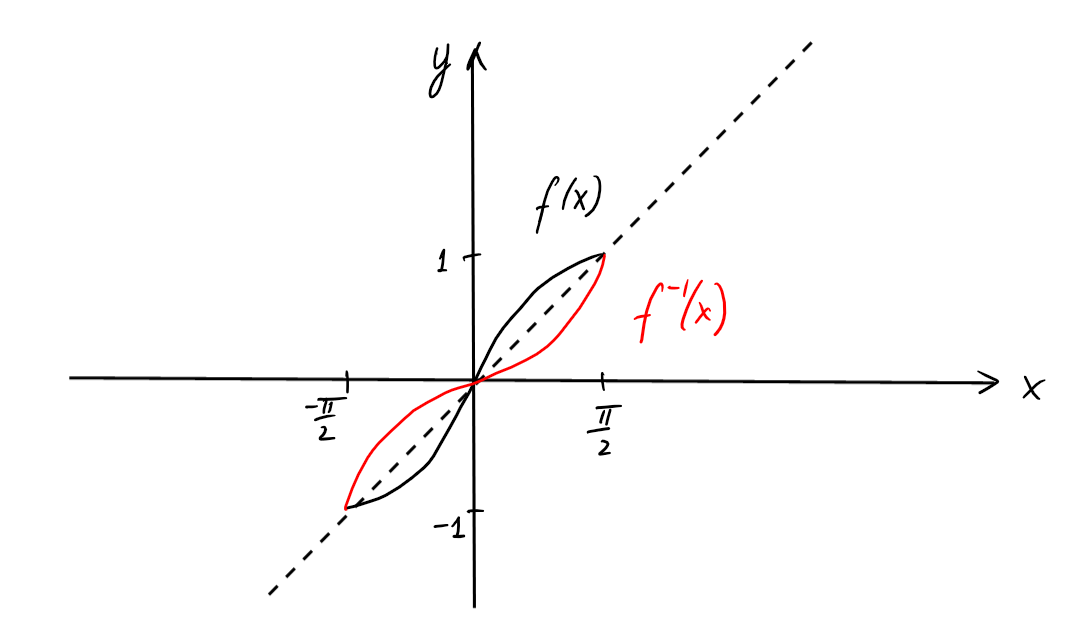
\(f: \mathbb{R} \rightarrow \mathbb{R}, \ x\mapsto \sin(x)\) n'est pas surjective (par ex. car \(y=2\) n'a pas de préimage).

\(f: \mathbb{R} \rightarrow [-1,1], \ x\mapsto \sin(x)\) est surjective mais pas injective (par ex. car \(\sin(0)=\sin(2\pi)\), mais \(0\neq 2\pi\)).

\(f: \left[\frac{-\pi}{2}, \frac{\pi}{2}\right] \rightarrow [-1,1], \ x\mapsto \sin(x)\) est bijective. Sa réciproque est \(f^{-1}:[-1,1]\rightarrow \left[\frac{-\pi}{2},\frac{\pi}{2}\right], y\mapsto \arcsin(y)\).

Exemple: Soit \(f:\mathbb{R} \rightarrow \mathbb{R}, \ x\mapsto x^2+2x-1\).

Cette fonction n'est pas surjective, par ex. car \(-3\) n'a pas de préimage. Par contre, \(f:\mathbb{R} \rightarrow [-2,\infty[, \ x\mapsto x^2+2x-1\) est surjective, puisque on a choisi l'image de \(f\) comme ensemble d'arrivée. Elle n'est toujours pas injective: par ex. \(f(-2)=-1=f(0)\). On peut restreindre l'ensemble de départ pour que la fonction devienne injective. Sur le graphe de \(f\), on voit qu'on peut choisir la ''partie droite'' de la parabole, ou la ''partie gauche'' de la parabole.

Si on choisit la partie droite, on obtient la fonction bijective \[\begin{aligned} f:[-1,\infty[&\rightarrow [-2,\infty[\\ x &\mapsto x^2+2x-1. \end{aligned}\] Sa réciproque est \[\begin{aligned} f^{-1}:[-2, \infty[ &\rightarrow[-1, \infty[\\ y &\mapsto f^{-1}(y)=-1+\sqrt{2+y}. \end{aligned}\] En effet, si \(y\in [-2,\infty[\), on a \[\begin{aligned} f(x)=y &\iff x^2+2x-1=y\\ &\iff x^2+2x-1-y=0\\ &\iff x = \frac{-2\pm \sqrt{4+4(1+y)}}{2} \end{aligned}\] et donc \(x=-1+\sqrt{2+y}\) puisque \(x\in [-1,\infty[\) (c'est-à-dire, \(x\geqslant -1\)).
De manière analogue, si on choisit la partie gauche, on obtient la fonction bijective \[\begin{aligned} f:]-\infty,-1]&\rightarrow [-2,\infty[\\ x &\mapsto x^2+2x-1 \end{aligned}\] dont la réciproque est \[\begin{aligned} f^{-1}:[-2, \infty[ &\rightarrow]-\infty,-1]\\ y &\mapsto f^{-1}(y)=-1-\sqrt{2+y}. \end{aligned}\]

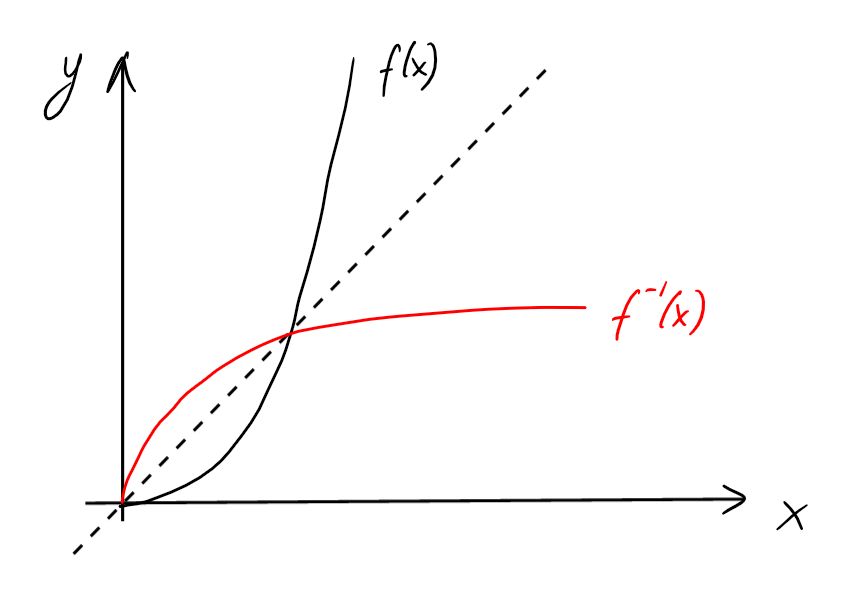
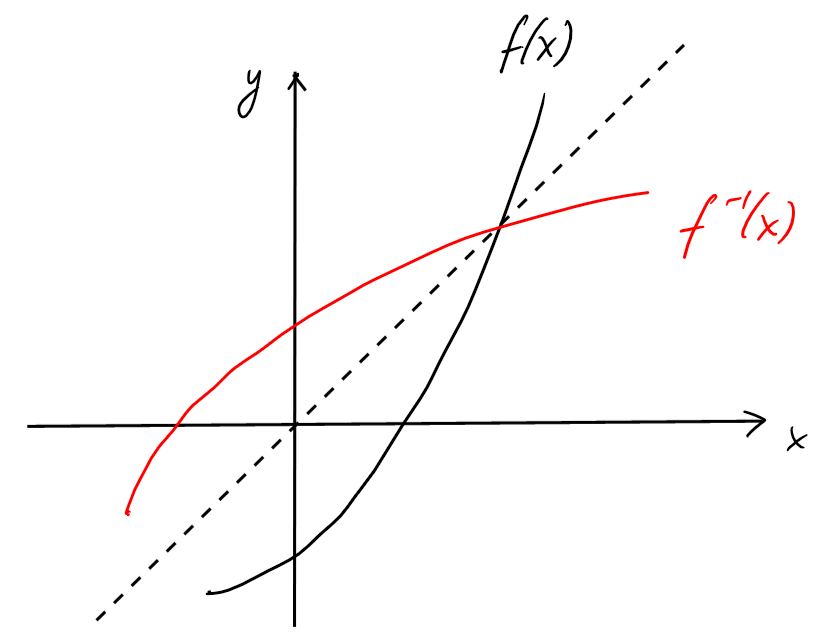
On remarque qu'on obtient le graphe de la fonction réciproque \(f^{-1}\) en reflétant le graphe de \(f\) par rapport à la diagonale \(y=x\).

2.4 Surjectivité, injectivité, bijectivité