2.1 Introduction
Une fonction \(f\) d'un ensemble \(A\) dans un ensemble \(B\) est une
règle qui assigne à chaque élément de \(A\) un unique élément de \(B\).
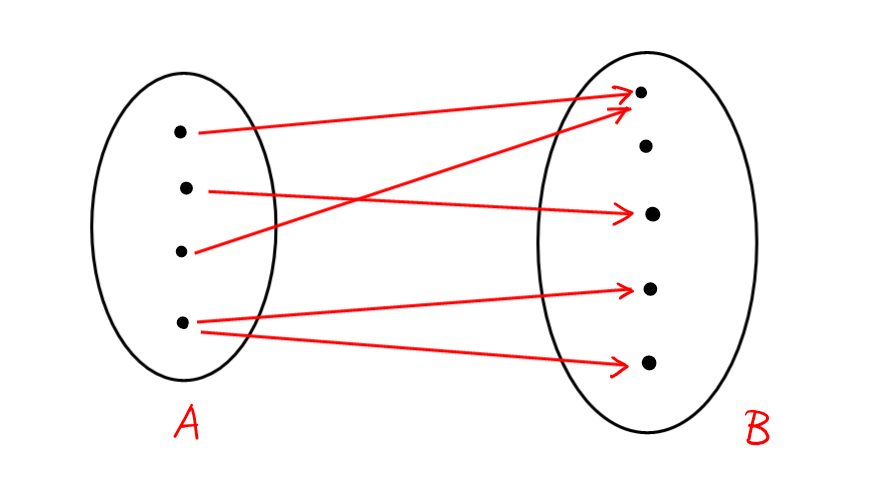
Si on représente par une flèche l'assignement de l'élément \(a\in A\) à
l'élément \(b\in B\),
On écrit \(f:A\rightarrow B\) et on note \(f(a)\) l'élément de \(B\) assigné à \(a\in A\). On écrit donc
\[\begin{aligned}
f:A&\rightarrow B\\
a &\mapsto f(a)
\end{aligned}\]
On dit que \(b=f(a)\) est l'image de \(a\) (\(a\) est
''envoyé sur/vers \(b\)''), et que \(a\) est une
préimage (ou un antécédent) de \(b\).
Exemple:
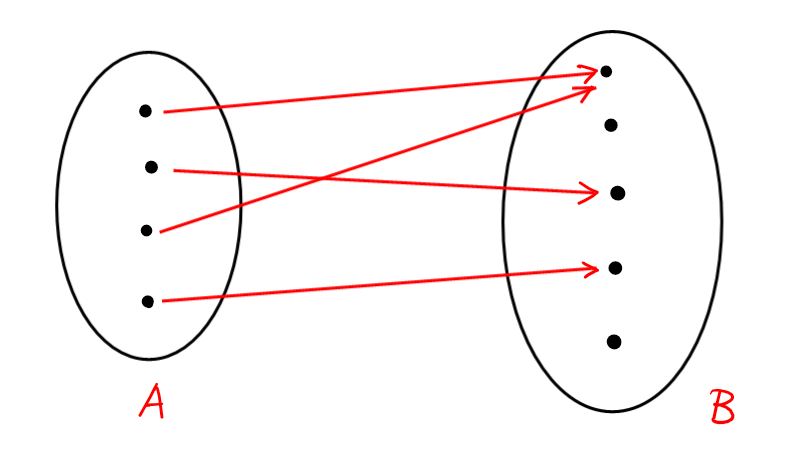
La règle représentée sur le shéma
ne définit pas une fonction, puisqu'il y a des éléments de \(A\) qui
sont envoyés vers plus qu'un élément de \(B\):
L'ensemble image \(\mathrm{Im} (f)\) de \(f\) est l'ensemble des éléments de \(B\)
qui possèdent au moins une préimage:
\[
\mathrm{Im} (f)=\{b\in B: \exists a\in A \text{ t.q. } f(a)=b\}\,.
\]
On parle d'une fonction réelle d'une variable réelle lorsque \(A\) et
\(B\) sont des sous-ensembles de \(\mathbb{R}\).
Au lieu de \(A\), on écrira souvent \(D_f\), et on parlera du
domaine de définition de \(f\).
Une fonction peut être décrite de plusieurs façons (on note que le domaine de
définition de la fonction fait partie, parfois implicitement, de la description
de la fonction):
- par une formule explicite
valable pour tout \(x\), par exemple \(f(x)=x^2\);
- par une distinction de cas, par exemple
\[
f(x)
=
\begin{cases}
5 &\text{ si }x\lt 1\,\\
42 &\text{ si }1\leqslant x\lt 2\,\\
1000 &\text{ si }x\geqslant 2
\end{cases}
\]
- verbalement, par des mots, par ex. la température en fonction du temps;
- graphiquement (par un graphe, voir ci-dessous).
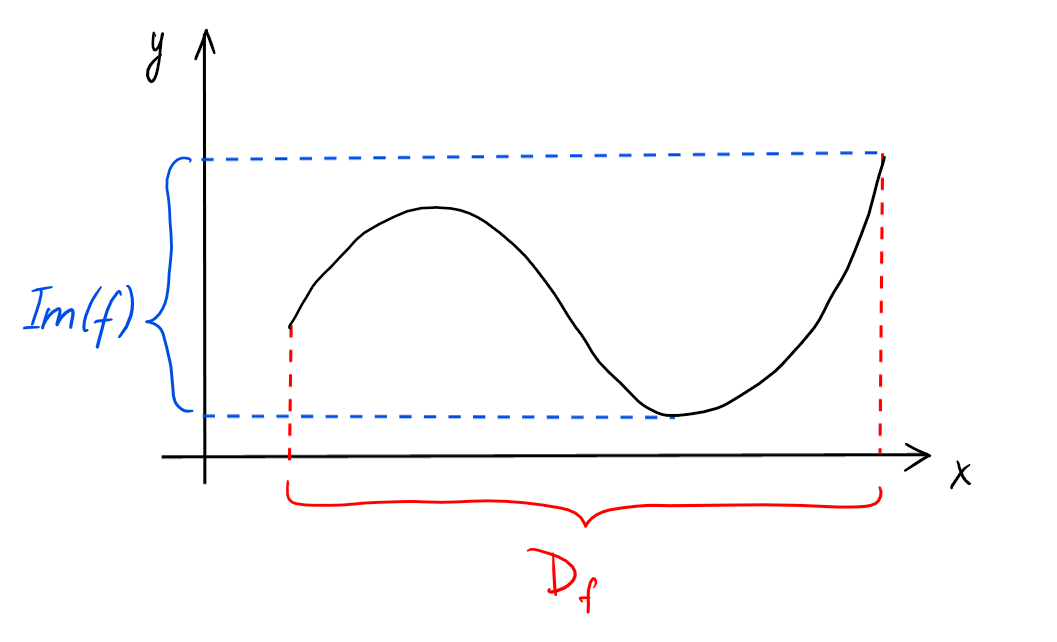
On peut se représenter plus facilement
une fonction \(f\) à l'aide de son graphe, qui est l'ensemble
\[
\{(x,y)\in \mathbb{R}^2: x \in D_f \text{ et } y=f(x)\}\,.
\]
Chaque point du graphe est donc de la forme \((x,f(x))\).
Ainsi, \(\mathrm{Im} (f)\) est l'ensemble des \(y\in \mathbb{R}\) pour lesquels la
droite horizontale de hauteur \(y\) coupe le graphe de \(f\) en au moins un
point.
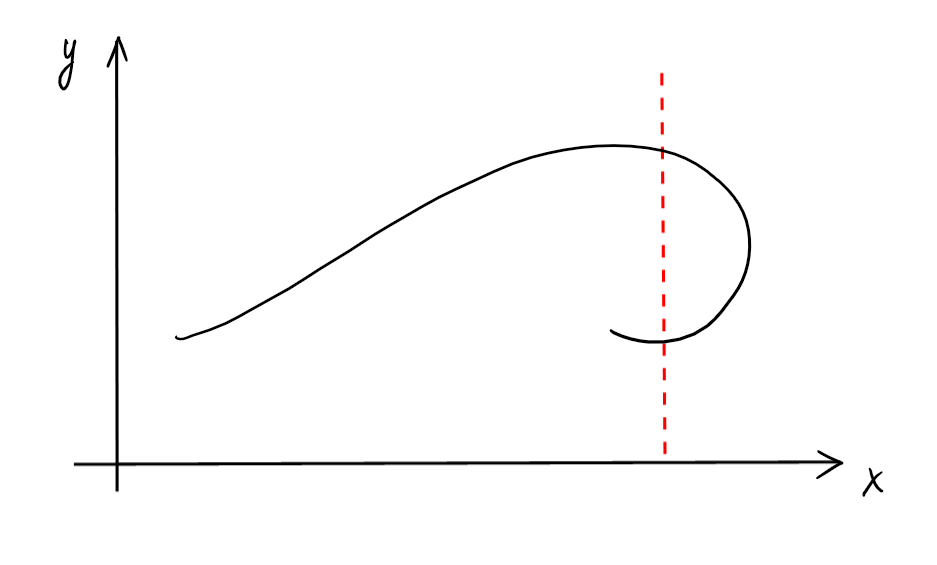
Remarquons qu'une courbe représente le graphe d'une
fonction seulement si toute droite
verticale la coupe au plus une fois.
Par exemple, l'image suivante ne représente pas le graphe d'une fonction:
Exemples:
- \(f: x\mapsto x^2\), \(D_f=\mathbb{R}\), \(\mathrm{Im} (f)=[0,\infty[\).
- \(f: x\mapsto |x|\), \(D_f=\mathbb{R}\), \(\mathrm{Im} (f)=[0,\infty[\).
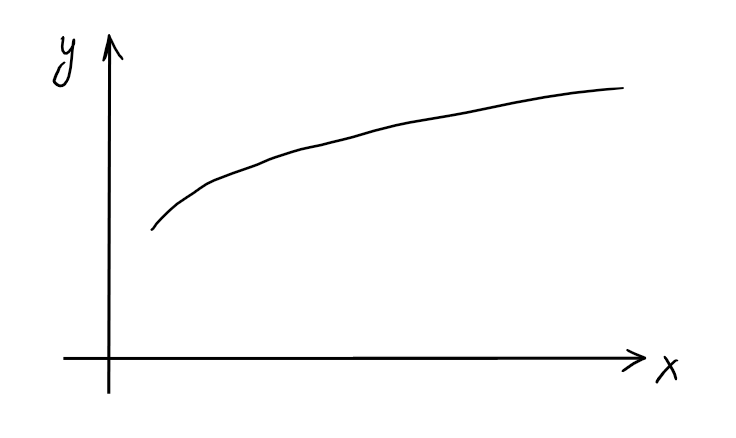
- \(f: x\mapsto \sqrt{x-1}+3\),
\(D_f=\{x\in \mathbb{R}: x-1\geqslant 0\} =[1,\infty[\), \(\mathrm{Im} (f)=[+3,\infty[\).
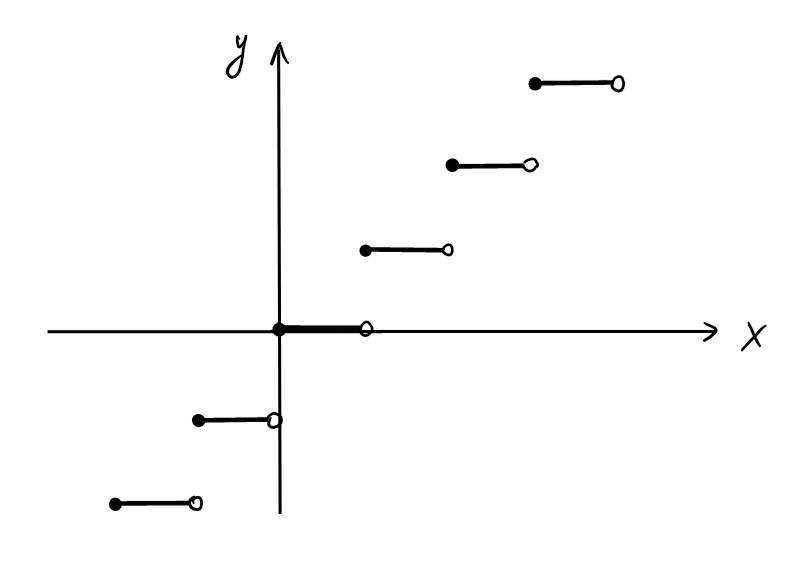
- \(E: x\mapsto E(x)\), où \(E(x)\) est
la partie entière de \(x\) (définie comme le plus grand entier \(n\in \mathbb{Z}\)
tel que \(n\leqslant x\)).
(Remarque sur l'image: un cercle plein indique la valeur de la fonction.)
Par exemple, \(E(0.5)=0\), \(E(-1.7)=-2\), \(E(5)=5\).
Ici, \(D_f=\mathbb{R}\) et \(\mathrm{Im} (f)=\mathbb{Z}\).
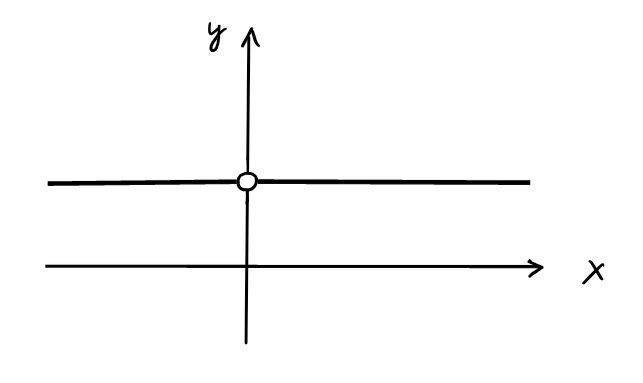
- \(f: x\mapsto \frac{x}{x}\),
\(D_f=\mathbb{R}\backslash\{0\}\), \(\mathrm{Im} (f)=\{1\}\).
Cette fonction vaut \(1\) partout, sauf en \(0\), où elle n'est pas définie.
Elle est donc différente de la fonction constante \(x\mapsto 1\) (qui est elle
définie partout).
Comment peut-on trouver \(\mathrm{Im} (f)\) sans connaître le graphe de \(f\) ? Comme
\(\mathrm{Im} (f)\) est l'ensemble des \(y\in\mathbb{R}\) tels qu'il existe \(x\in\mathbb{R}\) avec
\(f(x)=y\), on peut donc regarder pour quels \(y\) l'équation \(f(x)=y\) possède
une solution. L'ensemble de ces \(y\) sera alors l'image de \(f\).
Exemples:
- Pour trouver \(\mathrm{Im} (f)\) pour \(f(x)=\frac{1}{4x-6}\), on constate que
\[\begin{aligned}
y\in \mathrm{Im} (f)
&\iff \exists x\in\mathbb{R} \text{ t.q. } \frac{1}{4x-6}=y \\
&\iff \exists x\in\mathbb{R} \text{ t.q. } 1+6y=4xy.
\end{aligned}\]
Si \(y\neq 0\), on a la solution \(x=\frac{1+6y}{4y}\). Si \(y=0\), l'équation n'a pas de solution.
Donc \(\mathrm{Im} (f)=\mathbb{R}\setminus\{0\}=]-\infty, 0[ \ \cup \ ]0,+\infty[\).
- Pour trouver \(\mathrm{Im} (f)\) pour \(f(x)=x^2-4x\), on constate que
\[\begin{aligned}
y\in \mathrm{Im} (f) &\iff \exists x\in\mathbb{R} \text{ t.q. } x^2-4x=y\\
&\iff \exists x\in\mathbb{R} \text{ t.q. } x^2-4x-y=0\\
&\iff \Delta=16-4(-y)\geqslant 0\\
&\iff 16\geqslant -4y\\
&\iff y\geqslant -4.
\end{aligned}\]
Donc \(\mathrm{Im} (f)=[-4,\infty[\).