2.3 Composition de fonctions
La composée de deux fonctions \(f\) et \(g\), notée
\(g\circ f\), est définie
par
\[
(g\circ f)(x)=g(f(x))\,.
\]
Pour que le nombre \((g\circ f)(x)\) soit défini, il faut que \(x\in D_f\)
et que \(f(x)\in D_g\).
Graphes et compositions
On peut parfois déduire le graphe d'une fonction ''compliquée'', en
l'interprétant
comme une composition de fonctions ''simples'' dont on connaît le graphe. Il
est donc utile de savoir quel effet ont des compositions avec des fonctions
''simples'' sur le graphe d'une fonction.
On présente quelques cas simples. Une animation en bas de page permet de tester
l'effet de ces compositions.
Soit \(f\) une fonction quelconque.
-
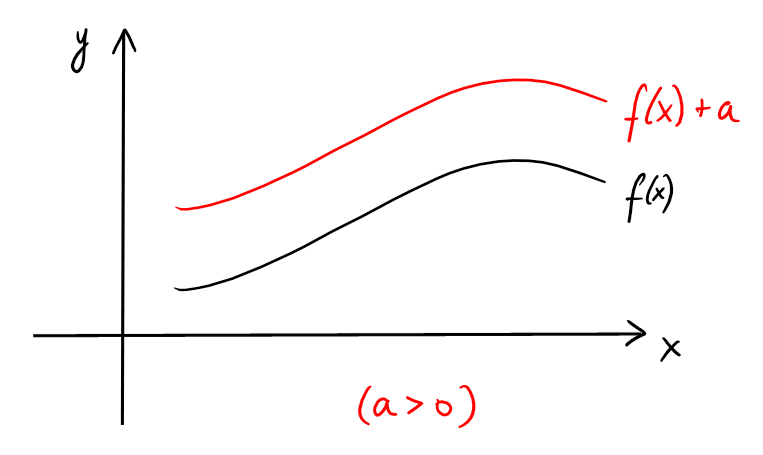
Si \(g(x)=x+a\), \((g\circ f)(x)=g(f(x))=f(x)+a\), et le
graphe de \(g\circ f\) est une translation verticale du graphe de \(f\), de
\(a\) unités, vers le haut si \(a\gt 0\), et vers le bas si \(a\lt 0\):
-
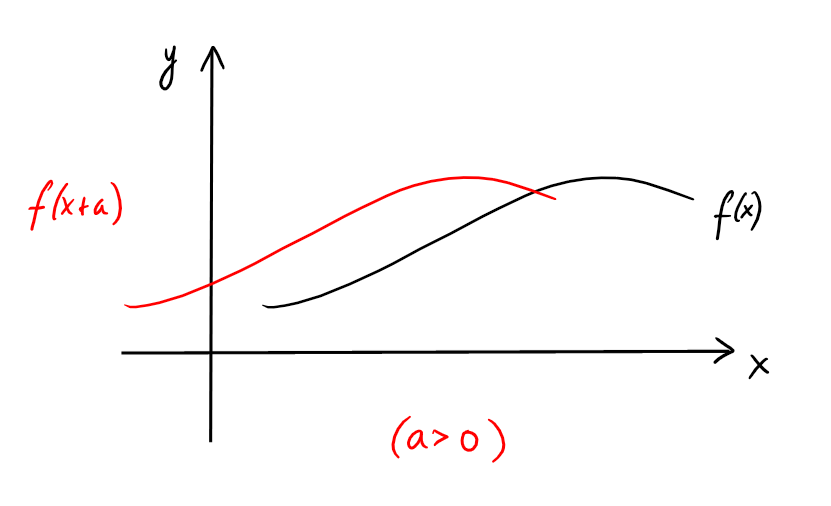
Si \(g(x)=x+a\), \((f\circ g)(x)=f(g(x))=f(x+a)\), et le graphe de
\(f\circ g\) est une translation horizontale
du graphe de \(f\), de \(a\) unités vers la gauche si \(a\gt 0\), vers la
droite si \(a\lt 0\):
La direction peut sembler un peu contre-intuitive. Pour se
convaincre, ça pourrait aider de réécrire
\((f\circ g)(x-a)=f(g(x-a))=f((x-a)+a)=f(x)\).
-
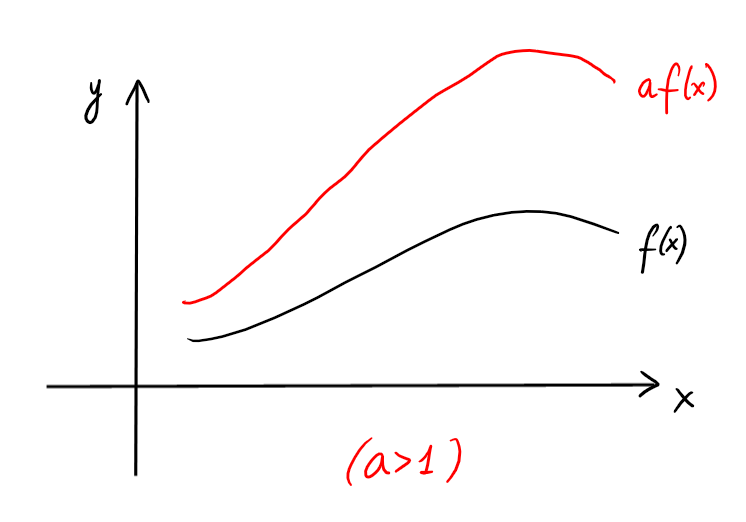
Si \(g(x)=ax\), \((g\circ f)(x)=g(f(x))=af(x)\),
et le graphe de \(g\circ f\) représente un étirement vertical de celui de \(f\):
-
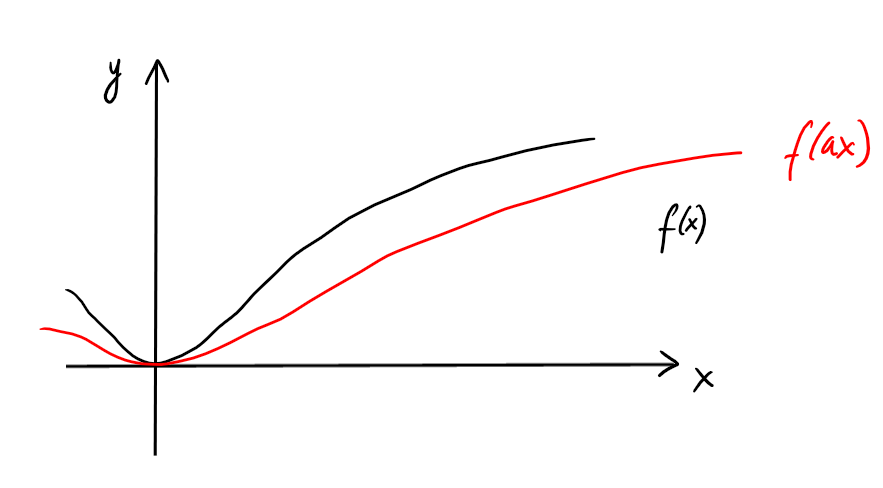
Si \(g(x)=ax\), \((f\circ g)(x)=f(g(x))=f(ax)\), et le graphe de \(f\circ g\)
est un étirement horizontal de celui de \(f\):
-
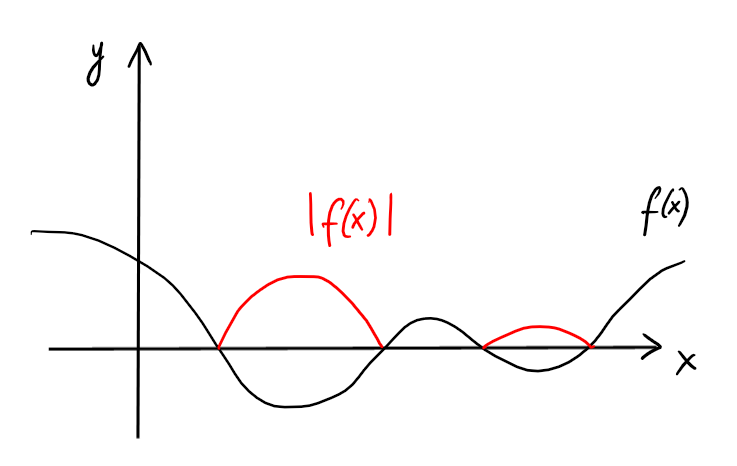
Si \(g(x)=|x|\), \((g\circ f)(x)=g(f(x))=|f(x)|\),
toute partie négative de la fonction est reflétée à travers l'axe \(Ox\):
Exemples:
-
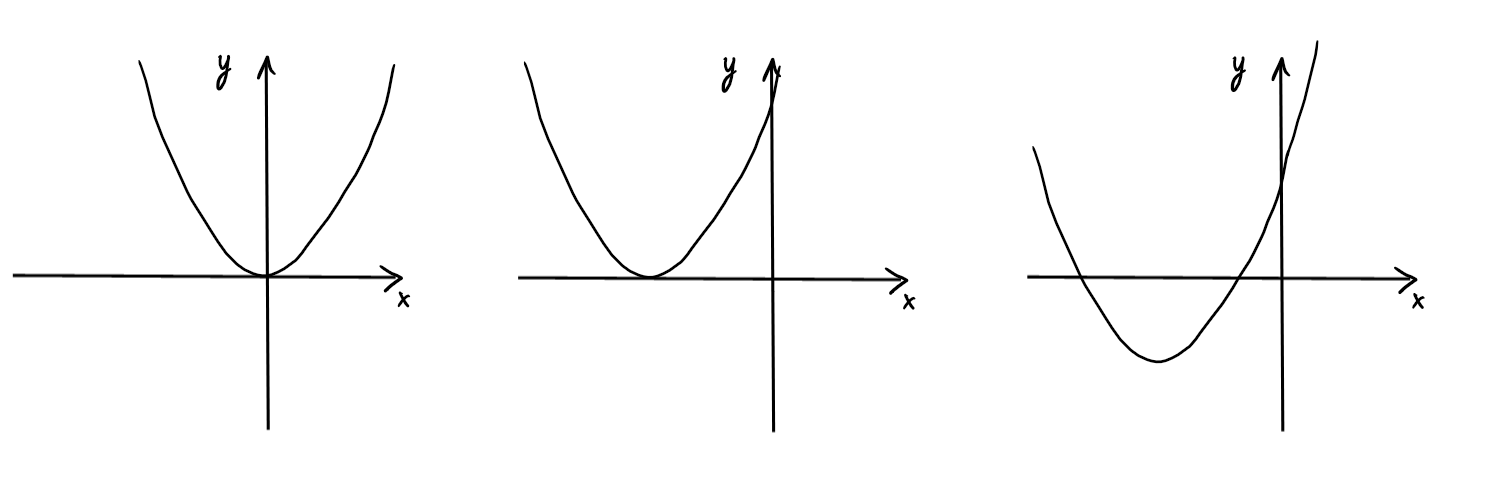
Pour esquisser le graphe de \(f(x)=x^2+6x+7\), on remarque que
\(f(x)=(x+3)^2-2\). C'est donc le graphe de \(x^2\), translaté vers la
gauche de 3 unités, puis translaté vers le bas de 2 unités.
-
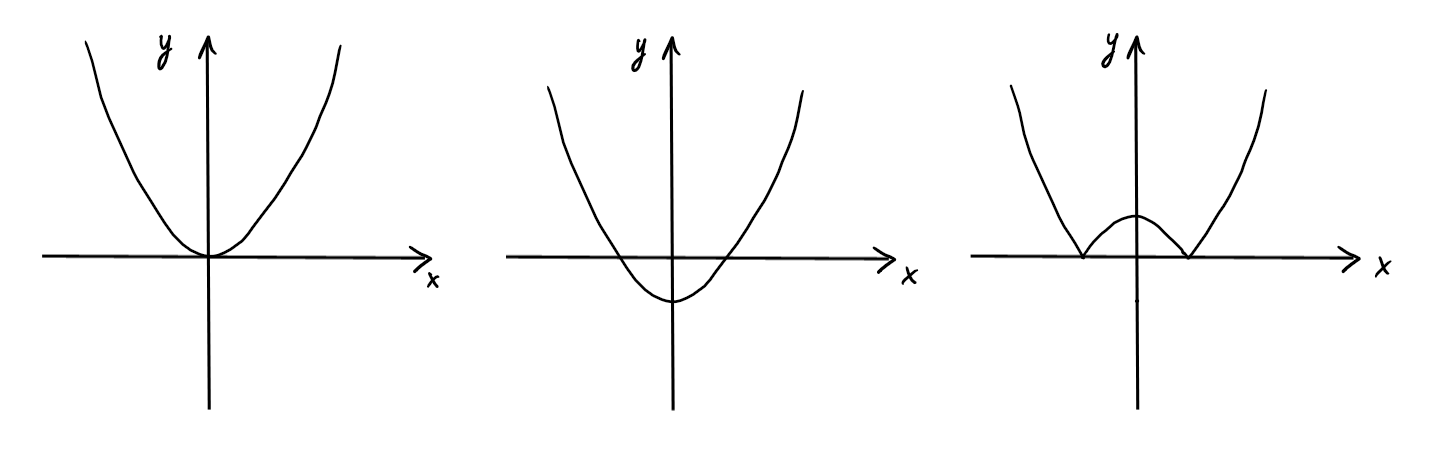
On peut dessiner le graphe de \(f(x)=|x^2-1|\) en décomposant la fonction en
trois étapes: \(x\mapsto x^2 \mapsto x^2-1 \mapsto |x^2-1|\).
Donc pour obtenir le graphe de \(f\), on prend le
graphe de \(x^2\), on le translate vers le bas d'une unité, puis on réfléchit la
partie négative à travers \(Ox\):
L'animation ci-dessous résume les différents types de transformations décrits
dans cette section: