5.4 Tangentes à des courbes dans \(\mathbb{R}^2\)
La dérivée d'une fonction évaluée en \(x_0\in \mathbb{R}\) nous donne la pente de la
tangente à la courbe définie par la fonction dans le plan au point
\((x_0,f(x_0))\). On peut utiliser la dérivée pour résoudre des problèmes
géométriques, comme ci-dessous.
Attention: il ne faut pas confondre la fonction dérivée avec l'équation de la
tangente !
Exemple:
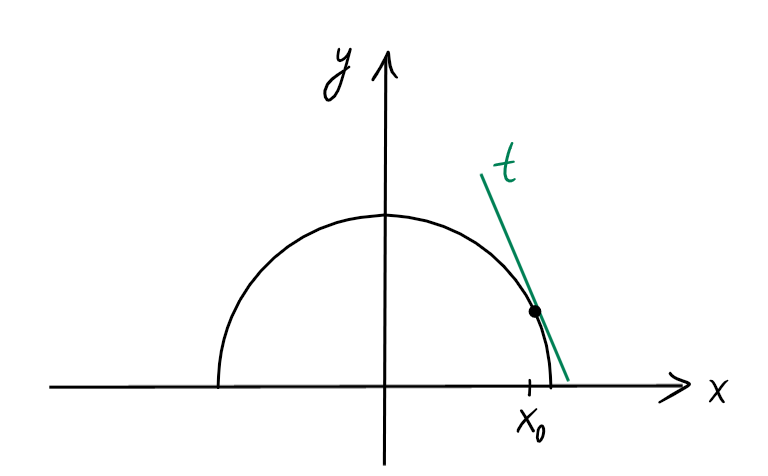
Soit \(f(x)=\sqrt{1-x^2}\), \(D_f=[-1,1]\).
Déterminons l'équation de la tangente \(t\) au graphe de \(f\) en
\(x_0=\frac{\sqrt{3}}{2}\). On sait que l'équation de \(t\) est donnée par
\[y=f'(x_0)(x-x_0)+f(x_0)\,.
\]
On a d'abord que
\[
f(x_0)
=\sqrt{1-\left(\frac{\sqrt{3}}{2}\right)^2}
=\sqrt{1-\frac{3}{4}}
=\sqrt{\frac{1}{4}}
=\frac{1}{2}\,,
\]
et puisque
\[
f'(x)
=\left[\left(1-x^2\right)^{\frac{1}{2}}\right]'
=\frac{\left(1-x^2\right)'}{2\sqrt{1-x^2}}
=\frac{-2x}{2\sqrt{1-x^2}}
=\frac{-x}{\sqrt{1-x^2}}\,,
\]
on peut calculer
\(f'(x_0)
=\frac{-\sqrt{3}/2}{\sqrt{1-\left(\frac{\sqrt{3}}{2}\right)^2}}
=-\sqrt{3}\).
L'équation de \(t\) est donc
\[
y=-\sqrt{3}\bigl(x-\tfrac{\sqrt{3}}{2}\bigr)+\frac{1}{2}\,.
\]
On peut aussi chercher des tangentes à une courbe sans connaître a priori le
point de tangence.
Exemple:
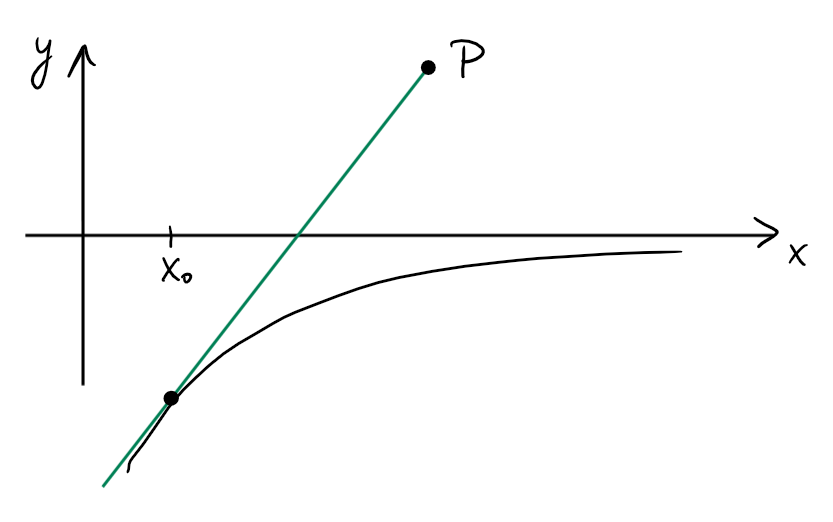
Soit \(f(x)=x-\sqrt{x^2+1}\).
Déterminons l'équation de la tangente \(t\) au graphe de \(f\) issue
du point \(P(2,1)\).
Il s'agit ici de déterminer le point de tangence \((x_0,f(x_0))\)
(où la tangente touche de graphe de \(f\)).
\(t\) a l'équation \(y=f'(x_0)(x-x_0)+f(x_0)\). Comme \(t\) passe par
\(P(2,1)\), on doit avoir
\(1=f'(x_0)(2-x_0)+f(x_0)\).
Résolvons cette équation pour trouver \(x_0\).
Il nous faut d'abord calculer la dérivée en un point quelconque:
\[f'(x)
=1-\frac{1}{2}\cdot \frac{2x}{\sqrt{x^2+1}}
=1-\frac{x}{\sqrt{x^2+1}}\Longrightarrow f'(x_0)
=1-\frac{x_0}{\sqrt{x_0^2+1}}\,.
\]
Ainsi, l'équation du dessus en \(x_0\) devient
\[\begin{aligned}
&1
=\bigl(1-\frac{x_0}{\sqrt{x_0^2+1}}\bigr)(2-x_0)
+\left(x_0-\sqrt{x_0^2+1}\right)\\
\iff&1=2-x_0-\frac{2x_0}{\sqrt{x_0^2+1}}
+\frac{x_0^2}{\sqrt{x_0^2+1}}+x_0-\sqrt{x_0^2+1}\\
\iff &-1=\frac{x_0^2-2x_0}{\sqrt{x_0^2+1}}-\sqrt{x_0^2+1}\\
\iff &-\sqrt{x_0^2+1}=x_0^2-2x_0-\left(x_0^2+1\right)\\
\iff &2x_0+1=\sqrt{x_0^2+1} \ (\text{et donc } 2x_0+1\geqslant 0)\\
\iff &(2x_0+1)^2=x_0^2+1 \text{ et } x_0\geqslant \frac{-1}{2}\\
\iff &4x_0^2+4x_0+1=x_0^2+1 \text{ et } x_0\geqslant \frac{-1}{2}\\
\iff &x_0(3x_0+4)=0 \text{ et } x_0\geqslant \frac{-1}{2}\\
\iff &x_0=0 \text{ car } \frac{-4}{3}\lt \frac{-1}{2}.
\end{aligned}\]
L'équation de \(t\) est donc
\[\begin{aligned}
y=f'(0)(x-0)+f(0)
&=\left(1-\frac{0}{\sqrt{0^2+1}}\right)x
+\left(0-\sqrt{0^2+1}\right)\\
&=x-1\,.
\end{aligned}\]
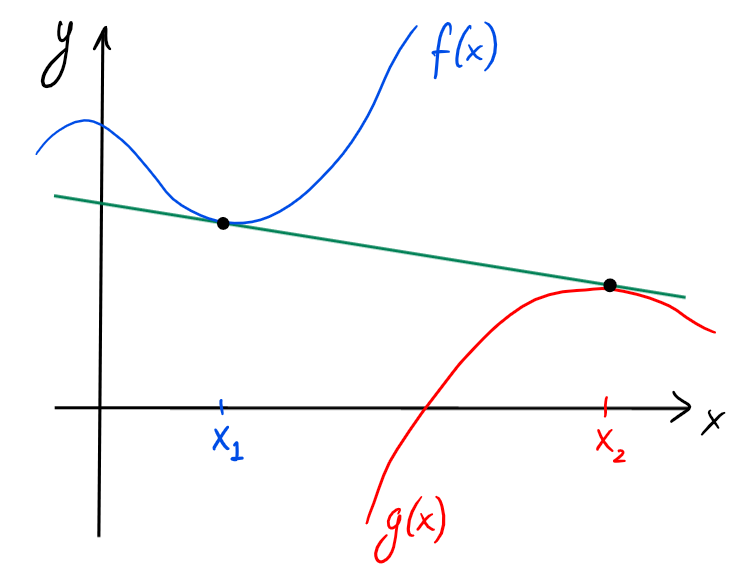
Tangente commune à deux courbes
Considérons deux fonctions \(y=f(x)\) et \(y=g(x)\), et considérons une tangente
commune à leurs graphes, c'est-à-dire une droite qui est tangente à la fois au
graphe de \(f\) et au graphe de \(g\):
Les points de tangence sont a priori distincts (comme sur l'image), on les nomme
\(x_1\) et \(x_2\),
Pour trouver l'équation \(y=mx+c\) de la tangente commune,
il faut que
\[m=f'(x_1)=g'(x_2)\,,
\]
et que les points
\((x_1,f(x_1))\) et \((x_2,g(x_2))\) soient tous deux sur la droite \(y=mx+c\).
Exemple:
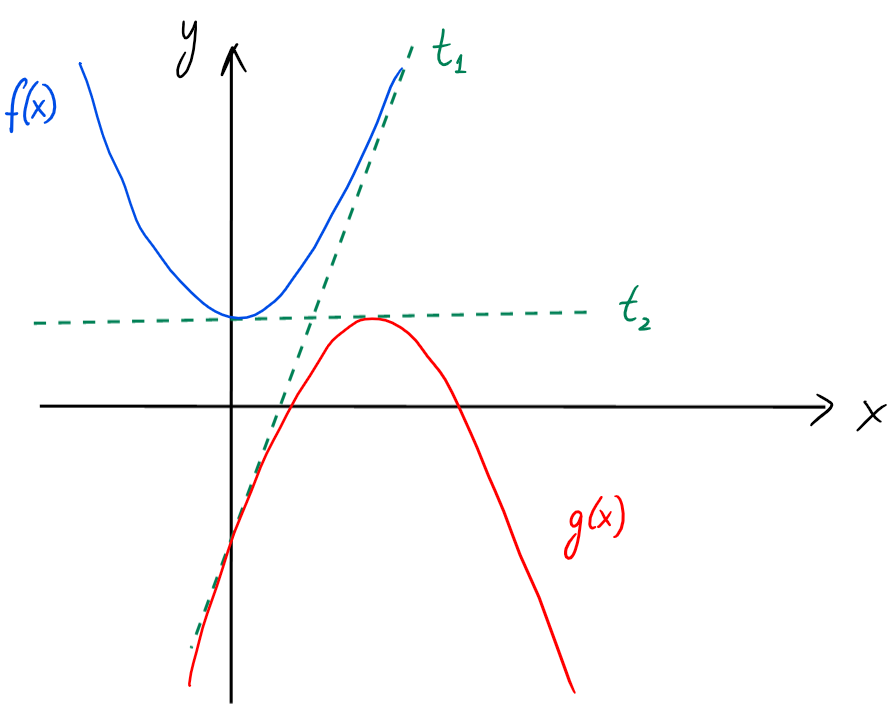
Cherchons les tangentes communes aux graphes des fonctions
\(f(x)=x^2+2\) et \(g(x)=-x^2+6x-7=-(x-3)^2+2\).
-
On a \(m=f'(x_1)=g'(x_2)\):
\[\begin{aligned}
m&= f'(x_1)=2x_1\\
m&=g'(x_2)=-2x_2+6.
\end{aligned}\]
On a donc \(2x_1=-2x_2+6 \iff x_1=-x_2+3\).
-
\((x_1,f(x_1))\) se trouve sur la tangente commune \(y=mx+c\):
\[\begin{aligned}
f(x_1)&=mx_1+c\\
x_1^2+2&=(2x_1)x_1+c\\
c&=-x_1^2+2.
\end{aligned}\]
-
\((x_2,g(x_2))\) se trouve sur la tangente commune \(y=mx+c\):
\[\begin{aligned}
g(x_2)&=mx_2+c\\
-x_2^2+6x_2-7&=(-2x_2+6)x_2+c\\
c&=x_2^2-7.
\end{aligned}\]
-
Les inconnues \(x_1,x_2,c\) doivent donc satisfaire
\[
\begin{cases}
x_1=-x_2+3\\
c=-x_1^2+2\\
c=x_2^2-7
\end{cases}
\]
On peut commencer par égaler la deuxième et la troisième équation, puis insérer
la première:
\[\begin{aligned}
-x_1^2+2=x_2^2-7\iff & -(-x_2+3)^2+2=x_2^2-7\\
\iff & 2x_2(x_2-3)=0.
\end{aligned}\]
On a donc deux solutions:
\[
x_2=0, x_1=3\qquad \text{ et }\qquad
x_2=3, x_1=0.
\]
Les deux tangentes communes sont donc
\[\begin{aligned}
t_1&: y=6x-7\\
t_2&: y=2.
\end{aligned}\]