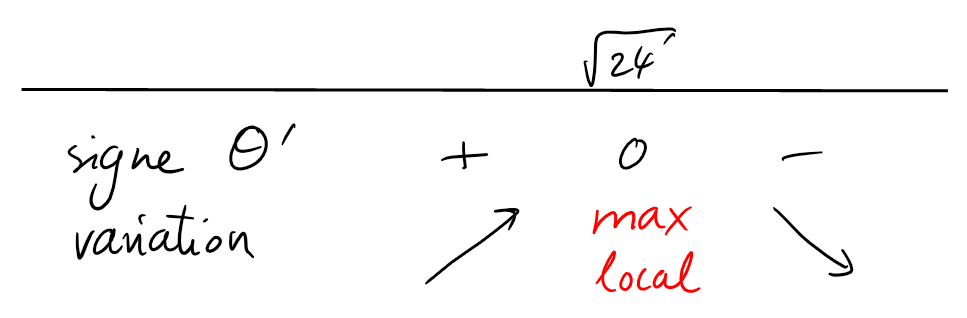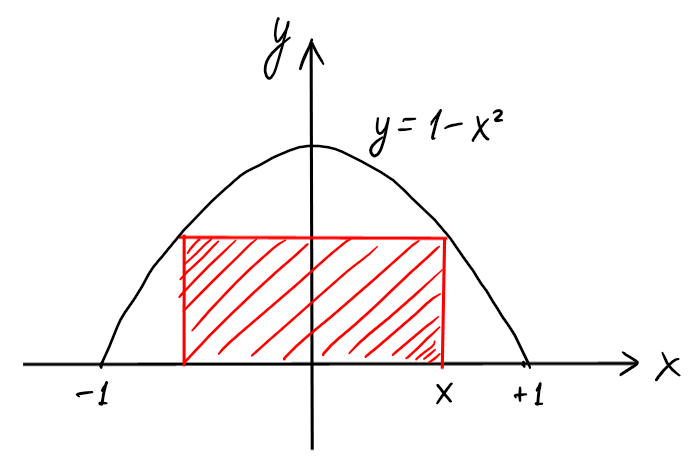
Exemple: Trouver le rectangle inscrit entre la courbe \(y=1-x^2\) et l'axe \(Ox\) d'aire maximale. (On suppose que les côtés du rectangle sont parallèles aux axes de coordonnées.)

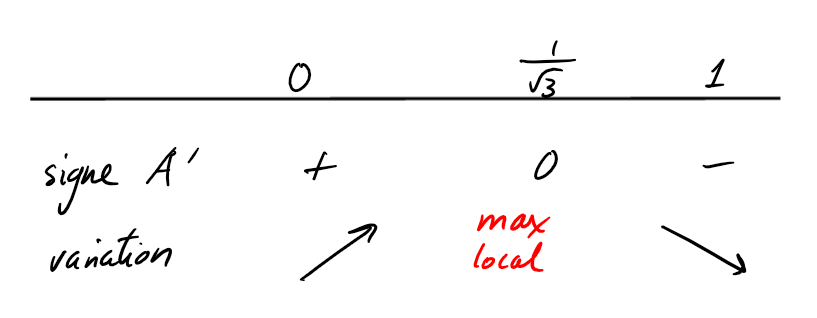
Paramétrisons tous les rectangles à l'aide de la variable \(x\in [0,1]\), visible sur l'image ci-dessus. Pour un \(x\) fixé, l'aire du rectangle représenté est égale à \[ A(x) =\text{ base } \times \text{ hauteur } =2x\cdot (1-x^2)\,. \] On aimerait donc trouver le maximum global de la fonction \[\begin{aligned} A:[0,1] & \to \mathbb{R}\\ x & \mapsto A(x)=2x(1-x^2)\,. \end{aligned}\] On a \(A'(x)=-6x^2+2\), et donc la variation de \(A\) est donnée par \(A\) s'annule sur le bord de \([0,1]\) bord, \(A(0)=A(1)=0\), et donc \(A\) possède un max local et global en \(x=\frac{1}{\sqrt{3}}\). En ce point, \(A\left(\frac{1}{\sqrt{3}}\right)=\frac{4}{3\sqrt{3}}.\)

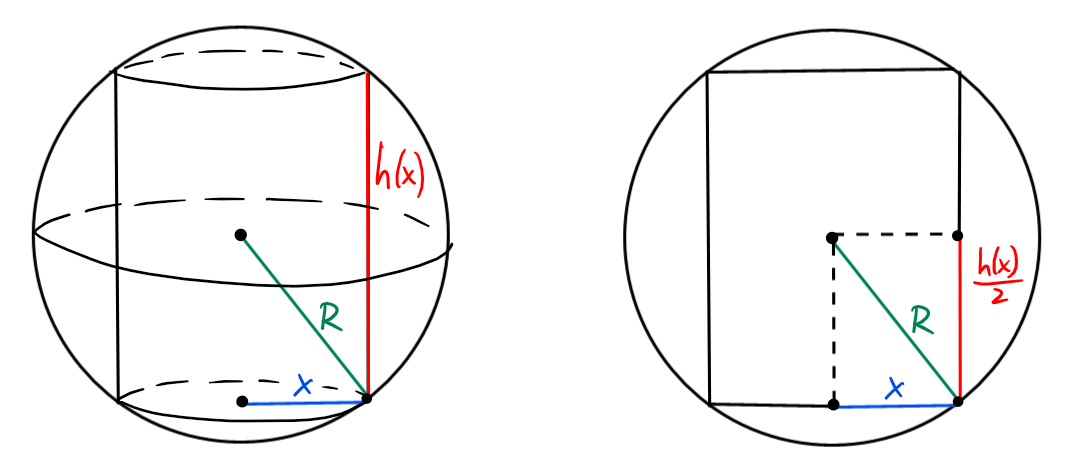
Exemple: Trouver, parmi tous les cylindres inscrits dans une sphère de rayon \(R\), celui dont le volume est maximal.

Utilisons la variable \(x\in [0,R]\) visible ci-dessus; \(x\) représente le rayon du cylindre inscrit.

Volume pour un \(x\) donné, \[ V(x)=\text{ aire de la base } \cdot \text{ hauteur } =\pi x^2 \cdot h(x)\,. \] On a \(x^2+\left(\frac{h(x)}{2}\right)^2=R^2\), d'où \(h(x)=2\sqrt{R^2-x^2}\).

On cherche donc le maximum global de \[\begin{aligned} V:[0,R] & \to \mathbb{R}\\ x & \mapsto V(x)=2\pi x^2\sqrt{R^2-x^2} \end{aligned}\] Or \[\begin{aligned} V'(x) &=2\pi\left(2x\sqrt{R^2-x^2}+x^2\cdot\frac{-2x}{2\sqrt{R^2-x^2}}\right)\\ &=2\pi\frac{2x(R^2-x^2)-x^3}{\sqrt{R^2-x^2}}\\ &=2\pi\frac{x(2R^2-3x^2)}{\sqrt{R^2-x^2}}\,. \end{aligned}\] On a donc, sur \(]0,R[\), que \[ V'(x)=0 \quad\iff\quad x=\sqrt{\frac{2}{3}}R\,. \] En ce point, \[ V\left(\sqrt{\frac{2}{3}}R\right)=\frac{1}{\sqrt{3}}\cdot\frac43\pi R^3\gt 0\,, \] alors que sur le bord, \(V(0)=V(R)=0\). On conclut donc que \(V\) possède un maximum global en \(x=\sqrt{\frac{2}{3}}R\). Le cylindre correspondant a un volume égale à \(\frac{1}{\sqrt{3}}=0.577\dots\) fois celui de la sphère.

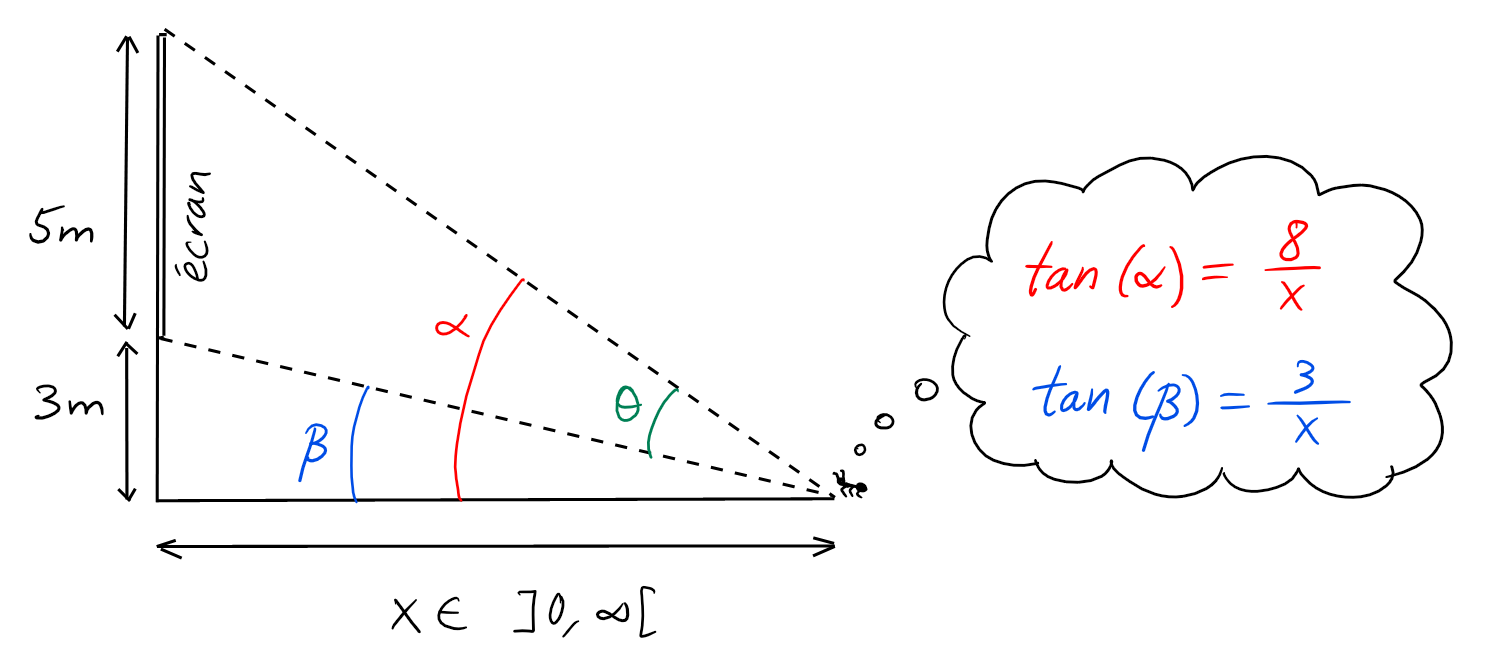
Exemple: Une fourmi au cinéma cherche à maximiser l'angle sous lequel elle voit l'écran:

Repérons la position de la fourmi à l'aide de \(x\in \ ]0,\infty[\), la distance (en mètres) entre la fourmi et le mur.

Lorsqu'elle est à distance \(x\) du mur, elle voit l'écran sous un angle \[ \theta(x) =\alpha(x)-\beta(x) =\arctan\left(\frac{8}{x}\right)-\arctan\left(\frac{3}{x}\right) \] On cherche donc le maximum global de \[\begin{aligned} \theta: \left]0,\infty\right[ & \to \mathbb{R}, \\ x & \mapsto \theta(x) =\arctan\left(\frac{8}{x}\right)-\arctan\left(\frac{3}{x}\right) \end{aligned}\] Remarquons que sur les bords du domaine, \[ \lim_{x\to 0^+}\theta(x) =\frac{\pi}{2}-\frac{\pi}{2}=0\,,\qquad \lim_{x\to +\infty}\theta(x)=0\,. \] Ensuite, sur \(]0,+\infty[\), \[\begin{aligned} \theta'(x)&=\frac{1}{1+\left(\frac{8}{x}\right)^2}\cdot \frac{-8}{x^2} -\frac{1}{1+\left(\frac{3}{x}\right)^2}\cdot \frac{-3}{x^2}\\ &=\frac{-8}{x^2+64}+\frac{3}{x^2+9}\\ &=\frac{-8x^2-72+3x^2+192}{(x^2+64)(x^2+9)}\\ &=\frac{120-5x^2}{(x^2+64)(x^2+9)}. 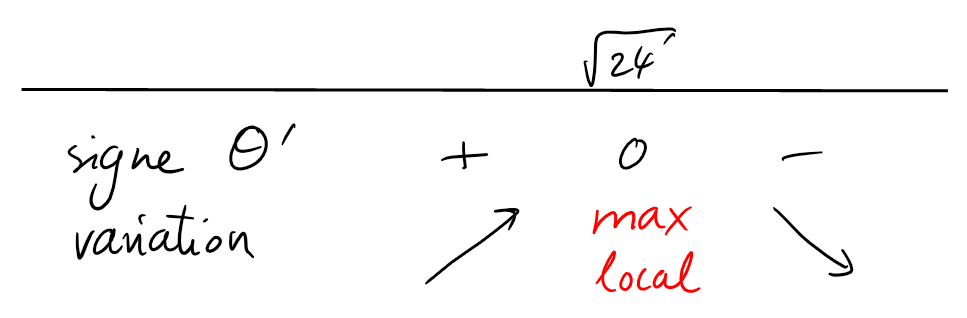\end{aligned}\] Ainsi, \(\theta'(x)=0 \iff x=\sqrt{24}\), et Puisque \(\theta(\sqrt{24})\gt 0\), on a donc un maximum global en \(x=\sqrt{24}\). Pour maximiser l'angle sous lequel elle voit l'écran, la fourmi doit donc s'asseoir à \(\sqrt{24}\) mètres de l'écran.