5.1 Définition et propriétés
Introduction
Étant donné une fonction \(f\) définie sur un voisinage de \(x_0\), une
information sur le taux de variation de \(f\)
sur l'intervalle \([x_0,x_0+h]\) est donnée par le quotient
\[
\frac{f(x_0+h)-f(x_0)}{(x_0+h)-x_0}=\frac{f(x_0+h)-f(x_0)}{h}\,,
\]
appelé le rapport de Newton de \(f\) en \(x_0\).
On pense à \(h\) comme un petit changement en \(x\).
Géométriquement, le rapport de Newton représente la pente de la droite sécante (en vert sur le dessin ci-dessous)
au graphe de \(f\), reliant les points
\((x_0,f(x_0))\) et \((x_0+h,f(x_0+h))\).
Remarque:
Si on imagine que
\(f(t)\) représente la distance parcourue par une particule jusqu'au
temps \(t\), le rapport de Newton
\[
\frac{f(t_0+h)-f(t_0)}{h}
\]
représente la vitesse moyenne entre les instants \(t_0\) et
\(t_0+h\). Plus \(h\) est petit, plus cette vitesse moyenne est proche de la
vitesse instantanée en \(x_0\).
Plus \(h\) est petit, plus l'information donnée par le rapport de Newton
sur la variation de \(f\) est précise.
On peut donc se poser la question:
Que se passe-t-il si on fait tendre \(h\to 0\) ?
Si \(f\) est continue, \((x_0+h,f(x_0+h))\) se rapproche de
\((x_0,f(x_0))\) à mesure que \(h\) se rapproche de zéro.
La limite du rapport de Newton représente donc une indétermination
''\(\frac{0}{0}\)''.
Listons quelques comportements possibles.
Lorsque \(h\to 0\), le rapport de Newton
\[
\frac{f(x_0+h)-f(x_0)}{h}
\]
peut...
- ... tendre vers une limite finie,
- ... tendre vers \(\pm \infty\),
- ... rester borné mais ne pas converger.
Considérons des exemples pour chacun de ces cas de figure.
Exemple:
\(f(x)=x^2\) est continue en \(x_0=2\) et
\[\begin{aligned}
\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}
&=\lim_{h\to 0}\frac{(2+h)^2-2^2}{h}\\
&=\lim_{h\to 0}\frac{4+4h+h^2-4}{h}\\
&=\lim_{h\to 0}(4+h)=4\,.
\end{aligned}\]
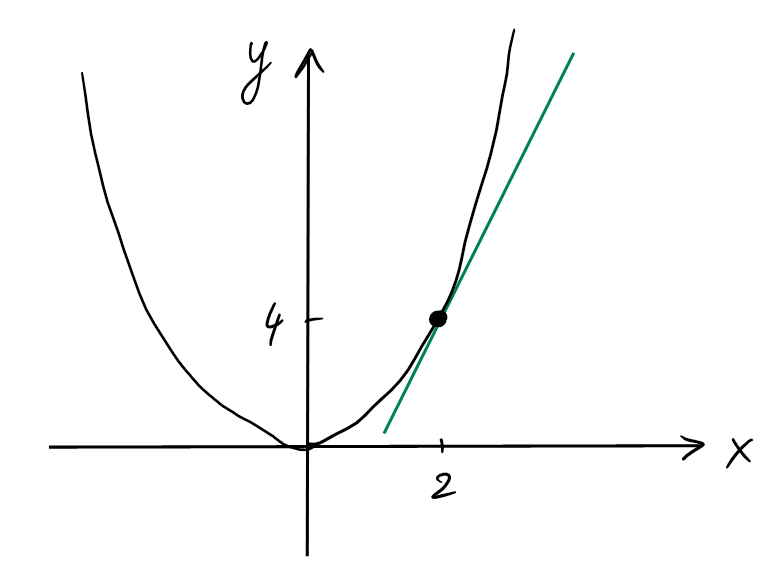
Géométriquement, la pente de la droite sécante
(reliant les points \((2,f(2))\) à \((2+h,f(2+h))\))
tend vers \(4\) lorsque \(h\) tend vers \(0\).
Exemple:
Considérons
\[
f(x)=
\begin{cases}
x\cdot\sin\left(\frac{1}{x}\right) & \text{ si } x\neq 0,\\
0 & \text{ si } x= 0\,,
\end{cases}
\]
qui est continue en \(x_0=0\) puisque
\[
\lim_{x\to 0}f(x)=0=f(0)\,,
\]
mais pour laquelle
\[
\frac{f(x_0+h)-f(x_0)}{h}
=\frac{h\cdot \sin\left(\frac{1}{h}\right)}{h}
=\sin\left(\frac{1}{h}\right)\,,
\]
qui est borné mais n'a pas de limite lorsque \(h\to 0\).
Géométriquement, la pente de la droite sécante oscille entre \(+1\) et \(-1\)
à mesure que \(h\) se rapproche de \(0\).
Exemple:
Considérons
\(f(x)=\sqrt[3]{x-1}\), qui est continue en \(x_0=1\) et
\[\begin{aligned}
\lim_{h\to 0}\frac{f(1+h)-f(1)}{h}
&=\lim_{h\to 0}\frac{\sqrt[3]{(1+h)-1}-\sqrt[3]{1-1}}{h}\\
&=\lim_{h\to 0}\frac{\sqrt[3]{h}}{h}\\
&=\lim_{h\to 0}\frac{1}{\sqrt[3]{h^2}}\\
&=+\infty\,.
\end{aligned}\]
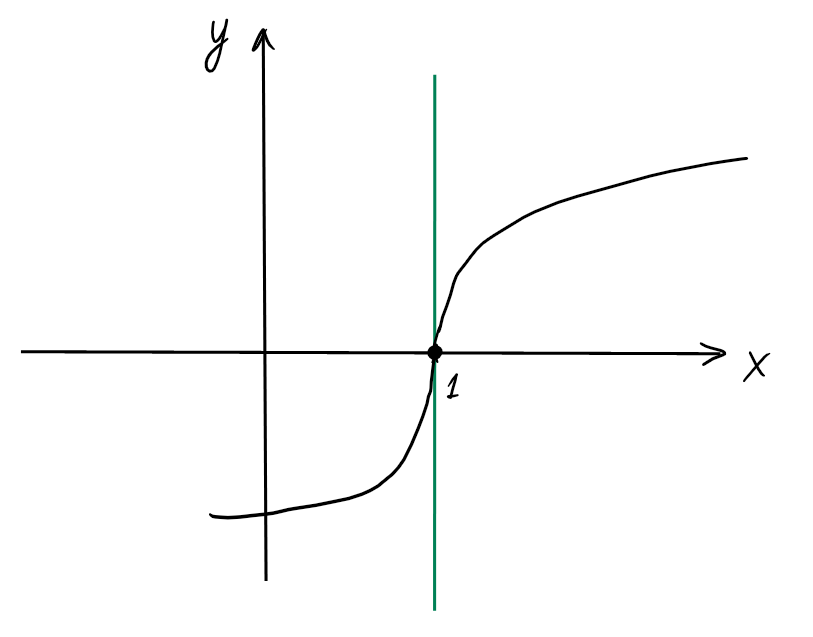
Géométriquement, la droite tangente au graphe de \(f\)
en \(1\) est verticale:
Définition
Soit \(f\) définie sur un voisinage de \(x_0\). \(f\) est
dérivable en \(x_0\) si la limite
\[
\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}
\]
existe (c'est-à-dire, est égale à un nombre réel).
Dans ce cas, cette limite est
appelée la dérivée (ou le nombre dérivé) de \(f\) en \(x_0\), et
on la note \(f'(x_0)\).
On peut écrire le nombre dérivé de diverses manières:
\[\begin{aligned}
f'(x_0)
&=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}\\
&=\lim_{\Delta x\to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\\
&=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}.
\end{aligned}\]
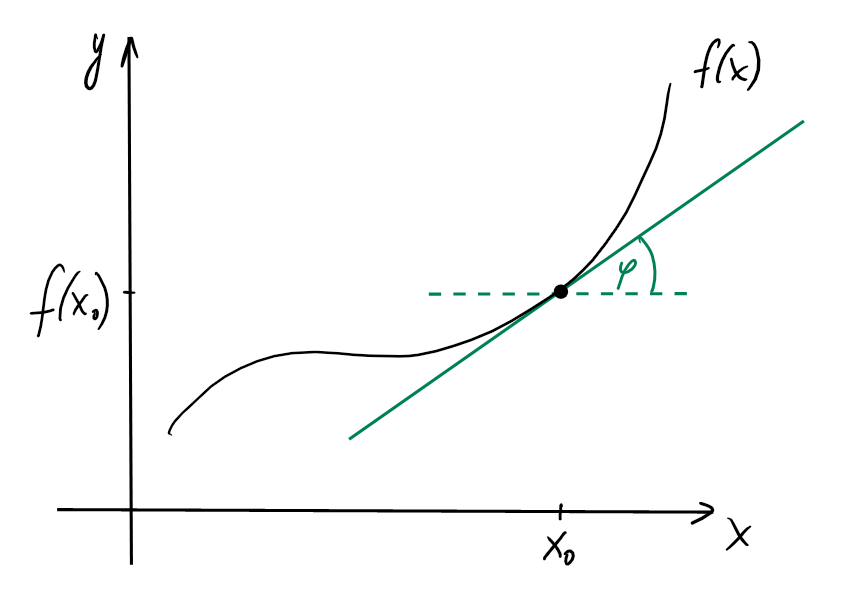
Géométriquement, l'existence de la dérivée \(f'(x_0)\) est équivalente à
l'existence d'une tangente au graphe de \(f\) au point \((x_0,f(x_0))\). En
effet, lorsque \(h\to 0\), la droite sécante tend vers la droite tangente
au point \(x_0\).
La pente de la tangente au graphe de \(f\) en \(x_0\) est donc
\[f'(x_0)=\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}=\tan(\varphi).\]
L'équation de la tangente au graphe de \(f\) en \(x_0\) est
\[y=f'(x_0)(x-x_0)+f(x_0),\]
qui est l'équation de la droite de pente \(f'(x_0)\) passant par le point
\((x_0,f(x_0))\).
Exemples:
- Prenons \(f(x)=x^2\) en \(x_0=2\). On a \(f(2)=4\) et \(f'(2)=4\) comme vu avant, et donc la tangente est donnée par
\[y=f'(x_0)(x-x_0)+f(x_0)=4(x-2)+4=4x-4.\]
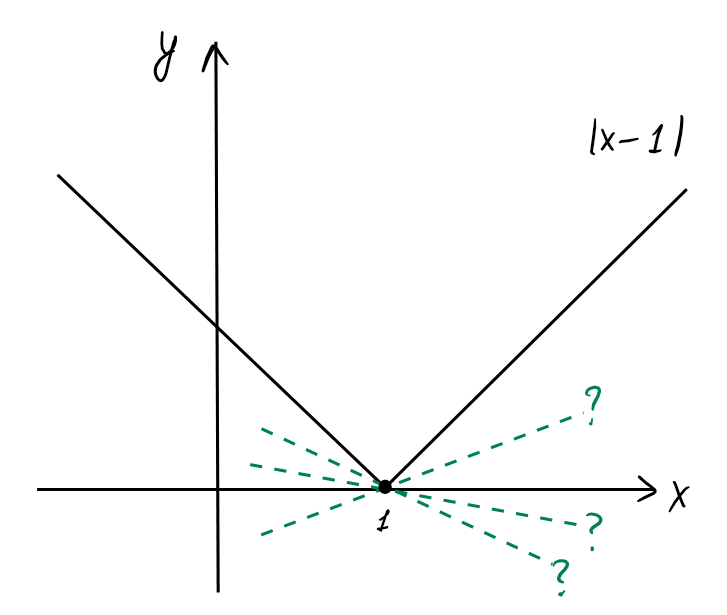
- Soit \(f(x)=|x-1|\). \(f\) n'est pas dérivable en \(x_0=1\). En effet, on a
\[\begin{aligned}
\lim_{x\to 1^+}\frac{f(x)-f(1)}{x-1}&=\lim_{x\to 1^+}\frac{(x-1)-0}{x-1}=1,\\
\lim_{x\to 1^-}\frac{f(x)-f(1)}{x-1}&=\lim_{x\to 1^-}\frac{-(x-1)-0}{x-1}=-1.
\end{aligned}\]
Donc la limite \(\lim_{x\to 1}\frac{f(x)-f(1)}{x-1}\) (et donc \(f'(1)\))
n'existe pas.
Effectivement, le graphe de \(f\) ne possède pas de tangente bien
définie en \(x_0=1\).
Dérivabilité latérale
Le dernier exemple le suggère: des limites latérales permettent d'introduire des
notions de dérivabilité latérale.
- Soit \(f\) définie sur un voisinage à gauche de \(x_0\).
Si
\[
f'_-(x_0):=\lim_{h\rightarrow 0^-}
\frac{f(x_0+h)-f(x_0)}{h}
\]
existe, on l'appelle la dérivée à gauche de \(f\) en \(x_0\).
- Soit \(f\) définie sur un voisinage à droite de \(x_0\).
Si
\[
f'_+(x_0):=\lim_{h\rightarrow 0^+}
\frac{f(x_0+h)-f(x_0)}{h}
\]
existe, on l'appelle la dérivée à droite de \(f\) en \(x_0\).
Géométriquement, ces dérivées latérales représentent les pentes des demi-droites
tangentes au graphe de \(f\) à gauche et à droite, au point \((x_0,f(x_0))\).
Théorème:
\(f\) est dérivable en \(x_0\) \(\iff\) \(f\) est dérivable à gauche et à droite
en \(x_0\), et \(f'_-(x_0)=f'_+(x_0)\).
Exemple:
Soit \(f:\mathbb{R}\to\mathbb{R}\) définie par
\[
f(x)=
\begin{cases}
(x^2+x+2)/2 &\text{ si }x\lt 0\,,\\
\sqrt{x+1}&\text{ si }x\geqslant 0\,.
\end{cases}
\]
On a \(f(0)=\sqrt{0+1}=1\), et donc
\[\begin{aligned}
f'_-(0)
=\lim_{h\to 0^-}\frac{f(h)-f(0)}{h}
&=\lim_{h\to 0^-}\frac{(h^2+h+2)/2-1}{h}\\
&=\lim_{h\to 0^-}\frac{h+1}{2}\\
&=\frac12\,,
\end{aligned}\]
et
\[\begin{aligned}
f'_+(0)=\lim_{h\to 0^+}\frac{f(h)-f(0)}{h}
&=\lim_{h\to 0^+}\frac{\sqrt{h+1}-1}{h}\\
&=\lim_{h\to 0^+}\frac{1}{\sqrt{h+1}+1}\\
&=\frac12\,.
\end{aligned}\]
Comme \(f'_-(0)=f'_+(0)=\frac12\), on en déduit par le théorème
que \(f\) est dérivable en \(x_0=0\) et que sa dérivée en ce point
vaut \(f'(0)=\frac{1}{2}\).
Exemple:
Soit \(f(x)=|x-1|\). On a vu plus haut que les
dérivées latérales en \(x_0=1\)existent, et que
\[
f'_-(1)
=-1\,,\qquad f'_+(1)=+1\,.
\]
Ainsi, \(f'_-(1)\neq f'_+(1)\), et par conséquent le théorème implique que
\(f\) n'est pas dérivable en \(1\).
Dérivabilité vs continuité
Théorème:
Si \(f\) est une fonction définie sur un voisinage de \(x_0\), alors
\[f \text{ est dérivable en }x_0
\quad \Longrightarrow \quad
f\text{ est continue en }x_0\,.
\]
L'implication est aussi vraie si on replace la dérivabilité et la continuité par
leurs analogues latéraux.
Preuve:
Supposons que \(f\) est dérivable en \(x_0\).
On a
\[\begin{aligned}
\lim_{x\to x_0}[f(x)-f(x_0)]
&=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\cdot (x-x_0)\\
&=\left(\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}\right)
\cdot
\left(\lim_{x\to x_0} (x-x_0)\right)\\
&=f'(x_0)\cdot 0\\
&=0.
\end{aligned}\]
On a donc \(\lim_{x\to x_0}f(x)=f(x_0)\): \(f\) est continue en \(x_0\).
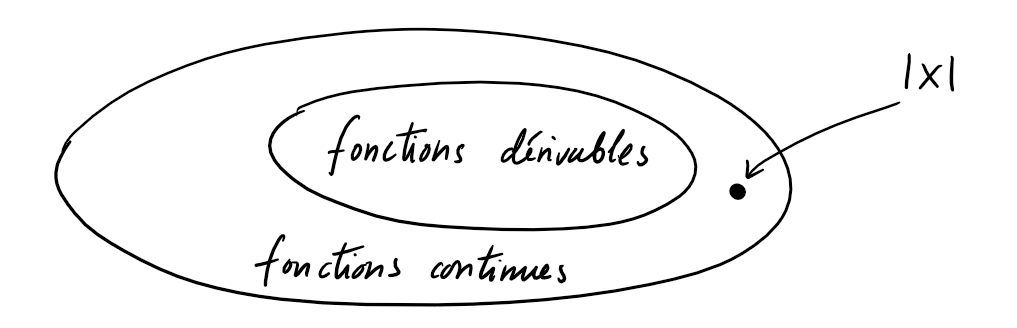
Attention: la réciproque du théorème
est fausse! Par exemple, la fonction \(f(x)=|x|\) est
continue au point \(x_0=0\) mais elle n'est pas dérivable en ce point.
Le théorème ci-dessus
nous montre que la continuité est une condition nécessaire pour
qu'une fonction soit dérivable. Mais il n'y a pas besoin de montrer séparément
la continuité; il suffit de montrer que la fonction est dérivable, et sa
continuité est immédiate par le résultat ci-dessus.