5.8 Extrema de fonctions
On a déjà donné les définitions d'extrema, à savoir
de maximum/minimum global/local dans une section précédente.
Remarque:
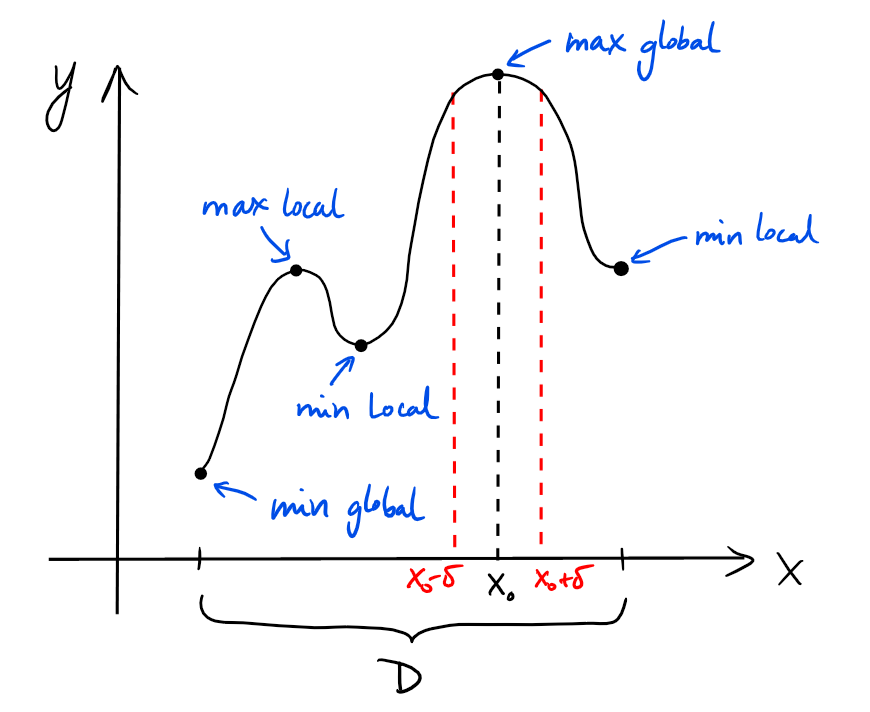
Un extremum global est aussi un extremum local. Par contre, un extremum local
n'est pas forcément global.
À titre d'illustration, voyons
quelques cas ''faciles'' de fonctions pour lesquelles les extrema peuvent
être trouvés sans difficulté.
Exemple:
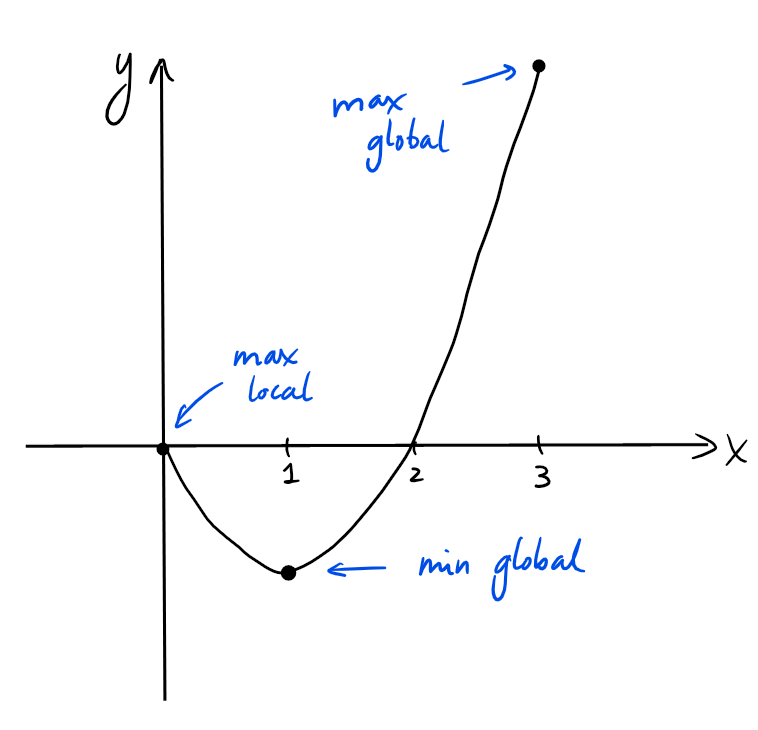
Soit \(f:[0,3]\to \mathbb{R}\), définie par \(f(x)=x^2-2x\).
Puisque \(f(x)=(x-1)^2-1\), on peut représenter la parabole précisément, et en
déduire que \(f\) possède:
- un minimum global en \(x=1\),
- un maximum global en \(x=3\),
- un maximum local en \(x=0\).
Exemple:
Soit
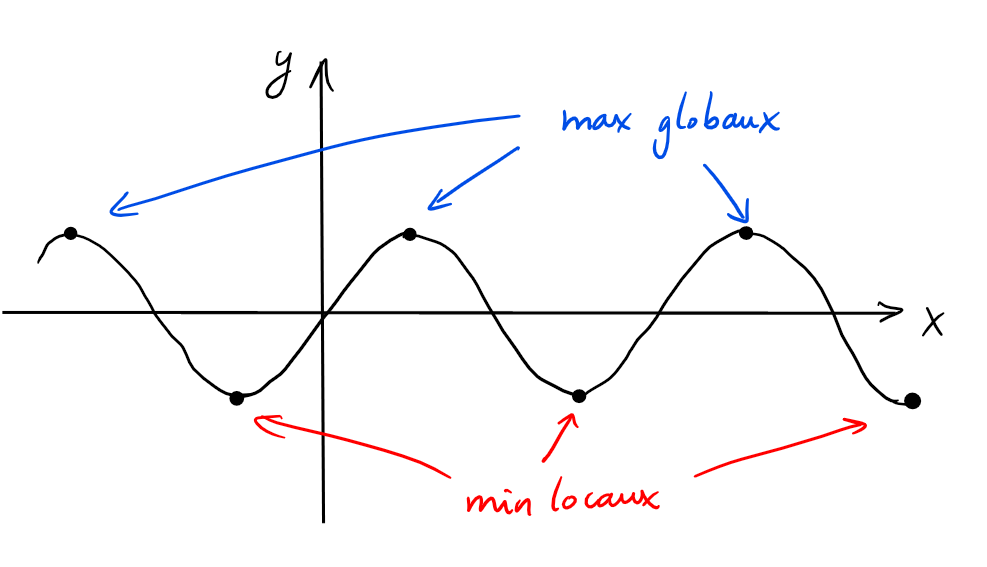
\(f:\mathbb{R} \to \mathbb{R}\), définie par \(f(x)=\sin(x)\).
\(f\) possède
- une infinité de maximums globaux, en \(\frac{\pi}{2}+2\pi k\), \(k\in \mathbb{Z}\),
- une infinité de minimums globaux, en \(-\frac{\pi}{2}+2\pi k\), \(k\in \mathbb{Z}\).
Exemple:
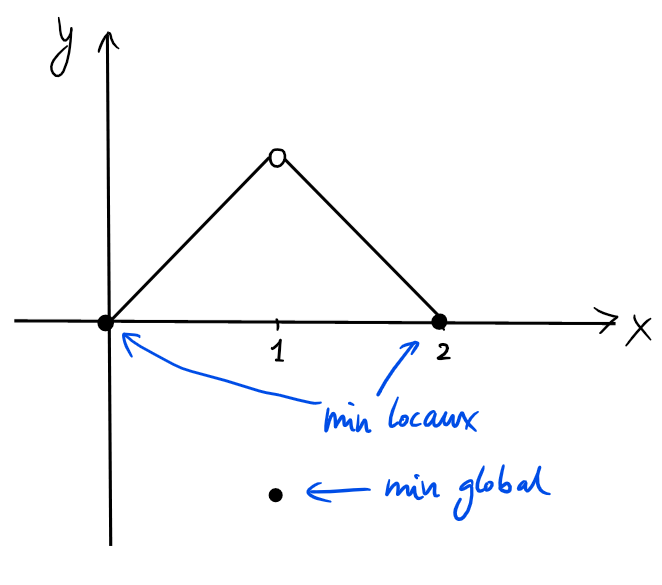
Soit \(f:[0,2]\to \mathbb{R}\), définie par
\[
f(x)=
\begin{cases}
1-|x-1| & \text{ si } x\neq 1,\\
-1 & \text{ si } x=1\,.
\end{cases}
\]
Alors \(f\)
- possède un minimum global en \(x=1\),
- possède deux minimums locaux en \(x=0\) et en \(x=2\),
- ne possède pas de maximum (ni local ni global).
Recherche analytique d'extrema
Comment peut-on trouver les extrema d'une fonction donnée, par des
méthodes analytiques?
Avant de chercher des extrema, il faudrait déjà être sûr que la fonction en
possède. Et rappelons que si la fonction est continue, et définie sur
un intervalle fermé et borné, \(f:[a,b]\to\mathbb{R}\), alors l'existence des
extrema globaux est garantie, ce qui est un bon point de départ, même si on a
besoin d'un algorithme plus précis qui mène à leur détermination.
Ensuite, on a
aussi vu le résultat suivant: pour une fonction dérivable \(f\) sur
\(]a,b[\), si \(f\) possède un minimum/maximum local en \(x_0\in
]a,b[\), alors \(f'(x_0)=0\). On a aussi noté que sa réciproque n'est pas vraie.
Donc si \(f'(x_0)=0\), alors \(x_0\) est un candidat
à être un minimum/maximum local.
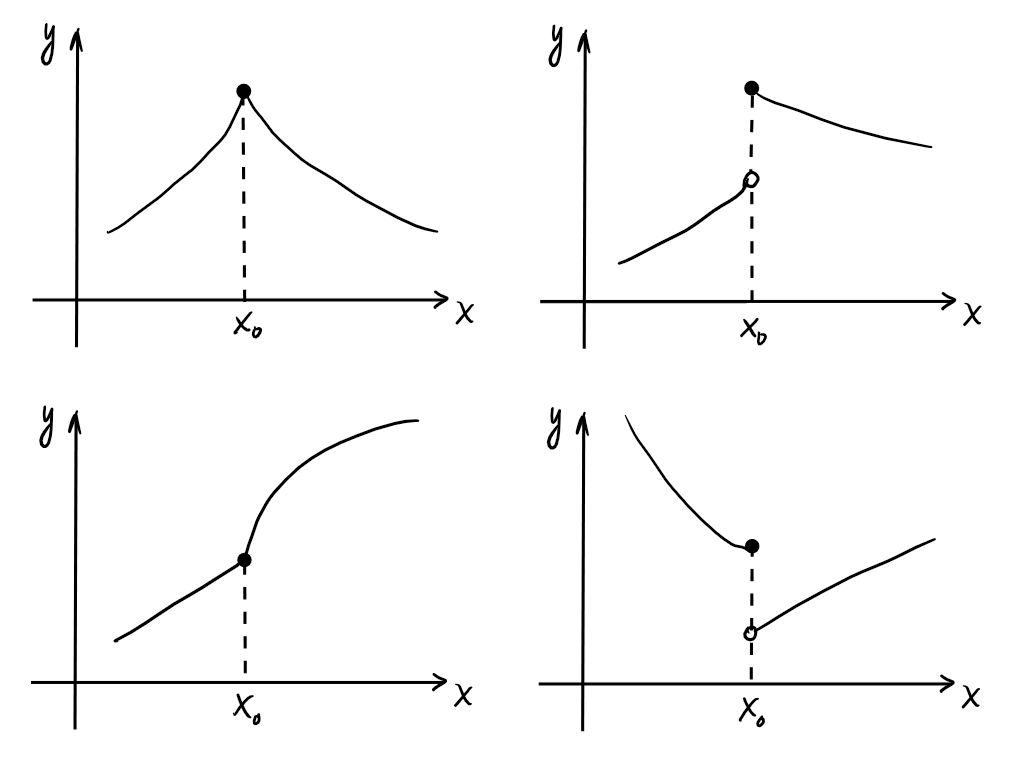
Mais si \(f\) n'est pas dérivable en \(x_0\), \(f\) peut y posséder un
minimum/maximum local, ou pas:
Pour trouver les candidats à être extrema locaux il faut
-
trouver les points \(x_0\) tels que \(f'(x_0)=0\),
-
trouver les points où \(f\) n'est pas dérivable,
-
regarder les points sur le bord du domaine, s'il y en a.
Ensuite on étudie la dérivée au voisinage du point, lorsque c'est possible, pour déterminer lesquels de ces candidats sont des extrema locaux.
Théorème:
Soit \(f\) continue en \(x_0\) et dérivable dans un voisinage épointé de
\(x_0\). Si \(f'\) change de signe en \(x_0\), alors \(f\) possède un extremum
local en \(x_0\).
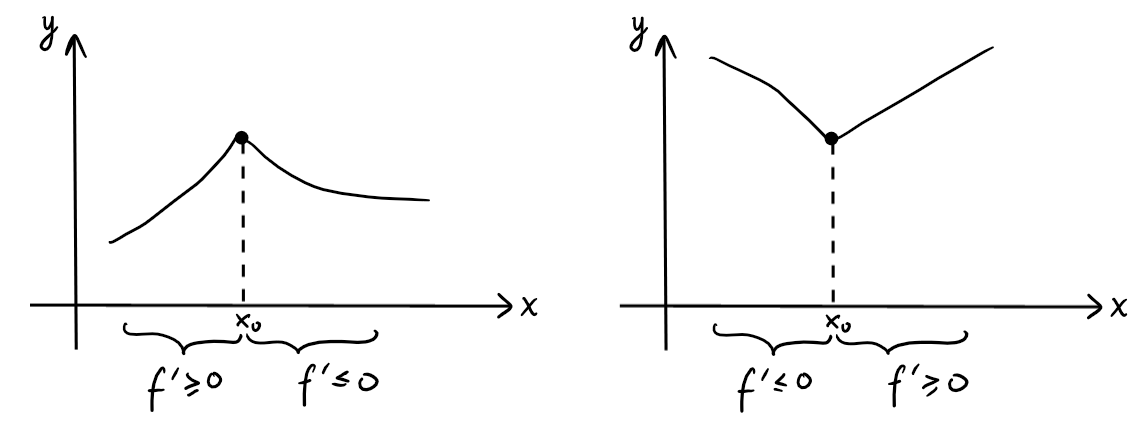
Par ''change de signe en \(x_0\)'', on veut dire qu'il existe \(\delta\gt 0\)
tel que
- \(f'(x)\geqslant 0\) pour tout \(x\in [x_0-\delta, x_0[\) et \(f'(x)\leqslant 0\) pour
tout \(x\in ]x_0,x_0+\delta]\)
(dans ce cas, il y a un max local en \(x_0\)),
ou
- \(f'(x)\leqslant 0\) pour tout \(x\in [x_0-\delta, x_0[\) et \(f'(x)\geqslant 0\)
pour tout \(x\in ]x_0,x_0+\delta]\)
(dans ce cas, il y a un min local en \(x_0\)).
Remarques:
-
Il faut vérifier la continuité de \(f\) en \(x_0\) ! Sinon, l'assertion du théorème pourrait être fausse. Par exemple, reprenons l'exemple précédent
\[f:[0,2]\to \mathbb{R}, f(x)=
\begin{cases}
1-|x-1| & \text{ si } x\neq 1,\\
-1 & \text{ si } x=1.
\end{cases}\]
\(f\) n'est pas continue en \(x_0=1\), et malgré le changement de signe de \(f'\) en \(x_0\), il n'y a pas de max en \(x_0\).
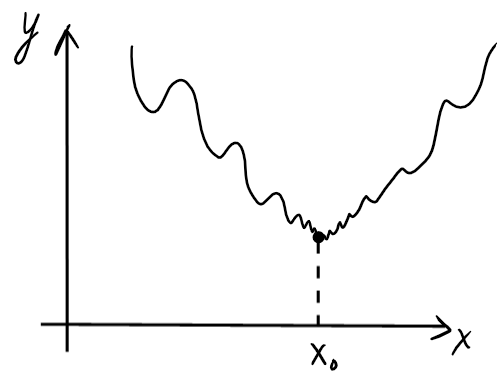
-
La réciproque du théorème est fausse: si \(f\) possède un extremum local en \(x_0\), \(f'\) ne change pas forcément de signe en \(x_0\).
Pour les extrema globaux, en vu du fait que les extrema globaux sont aussi des
extrema locaux, il faut juste évaluer la fonction aux points qu'on a trouvés
ci-dessus comme extrema locaux, et trouver parmi eux les plus grandes et les
plus petites valeurs.
Rappel: une fonction continue atteint ses bornes sur un intervalle fermé.
Exemples:
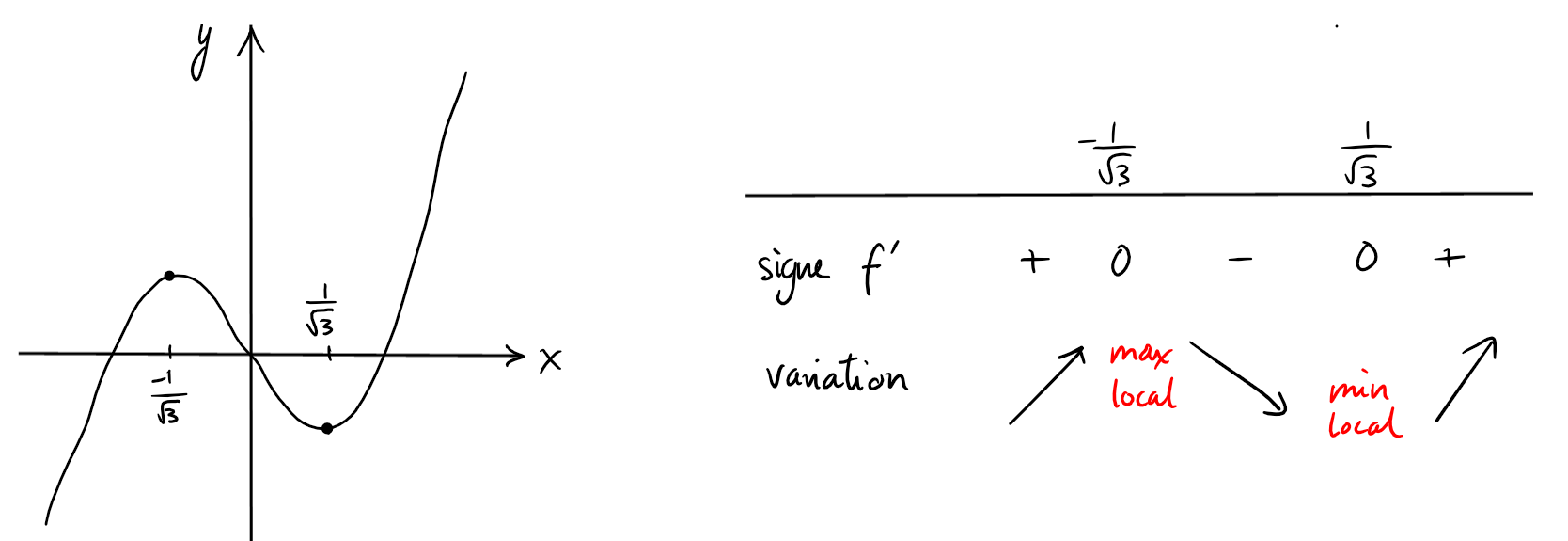
-
\(f:\mathbb{R} \rightarrow \mathbb{R}\), \(f(x)=x^3-x\).
\(f'(x)=3x^2-1\) et donc \(f'(x)=0\iff x=\frac{\pm 1}{\sqrt{3}}\).
Il n'y a pas d'extrema globaux.
-
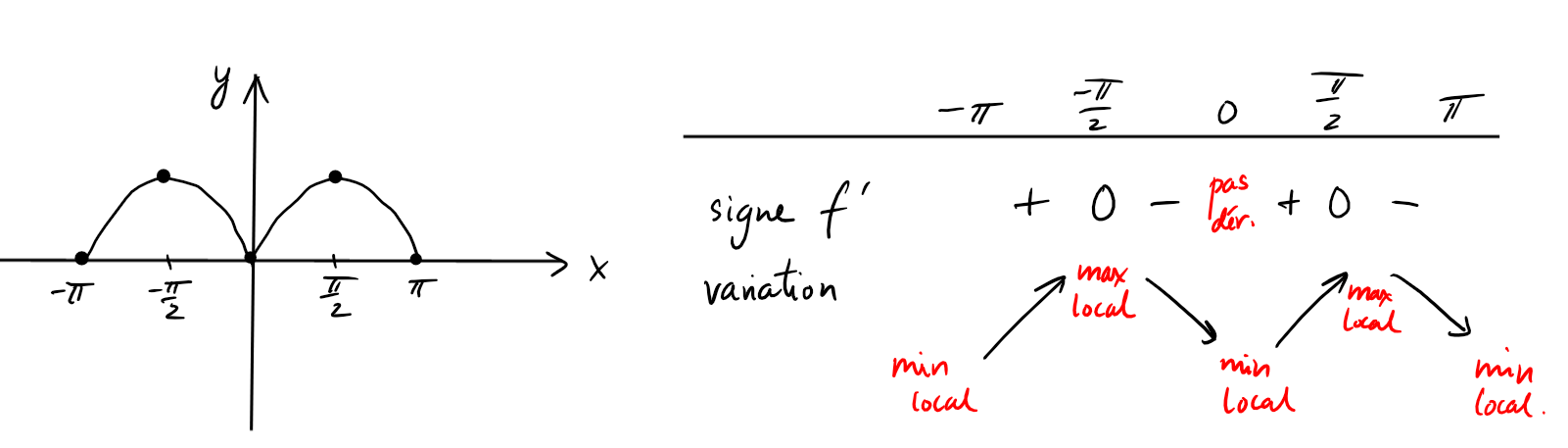
\(f:[-\pi,\pi]\to \mathbb{R}\), \(f(x)=\sin|x|\).
On a \(f(x)=
\begin{cases}
\sin(x) & \text{ si } 0\leqslant x \leqslant \pi\\
\sin(-x) & \text{ si } -\pi\leqslant x \lt 0,
\end{cases}\)
et donc, puisque \(\sin(-x)=-\sin(x)\),
\(f'(x)=
\begin{cases}
\cos(x) & \text{ si } 0\lt x \lt \pi\\
-\cos(x) & \text{ si } -\pi \lt x \lt 0.
\end{cases}\)
En \(0\), on a
\[\begin{aligned}
f'_+(0)
&= \lim_{x\to 0^+} \frac{f(x)-f(0)}{x-0}
=\lim_{x\to 0^+}\frac{\sin(x)}{x}=1,\\
f'_-(0)
&= \lim_{x\to 0^-} \frac{f(x)-f(0)}{x-0}
=\lim_{x\to 0^-}\frac{-\sin(x)}{x}=-1,
\end{aligned}\]
et donc \(f\) n'est pas dérivable en \(0\).
Les candidats sont
-
\(x=\pm \frac{\pi}{2}\) (\(\iff f'(x)=0\)),
-
\(x=0\), où \(f\) n'est pas dérivable,
-
\(x=\pm \pi\), les points du bord.
Ici, les extrema locaux sont aussi globaux.