Analyse B (MAN)

5.10 Études de fonctions

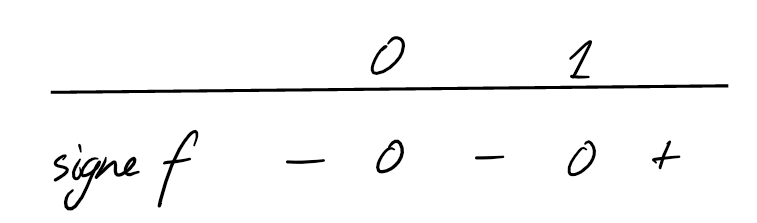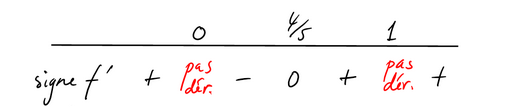
Généralement, l'étude d'une fonction \(f\) signifie décrire les principales caractéristiques de la dépendence de \(f(x)\) en fonction de \(x\), qu'elles soient locales ou globales, autant du point de vue quantitatif que qualitatif.

Les sections précédentes ont montré comme la dérivée se présente comme un outil puissant pour l'analyse locale.

Avant de passer en revue les principaux éléments que peuvent constituer une étude de fonction, introduisons certaines notions additionnelles.

Branches infinies

Parmi les propriétés globales caractéristiques d'une fonction, on peut considérer les portions de son graphe, s'il y en a, qui contiennent des points arbitrairement éloignées de l'origine. On parle alors de branches infinies.

Commençons par les branches infinies données par directement par l'étude simple de limites à l'infini, ou proche d'un point \(x_0\).

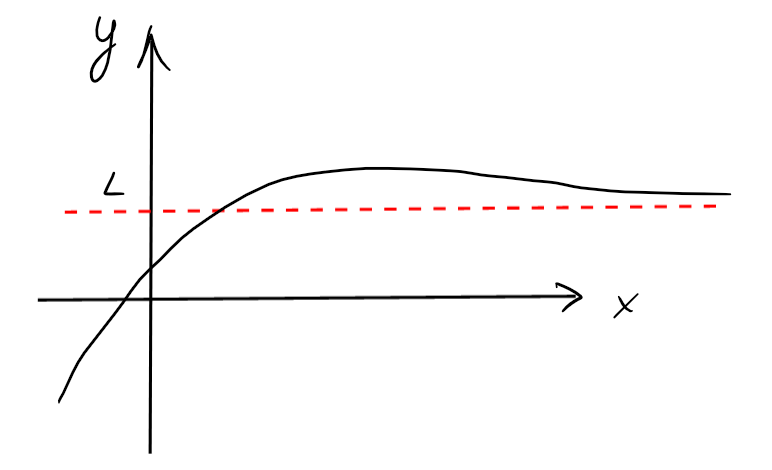
Si au moins une des limites \(\lim_{x\to x_0^+}f(x)\), \(\lim_{x\to x_0^-}f(x)\) est \(\pm \infty\), on dit que la droite verticale d'équation \(x=x_0\) est une asymptote verticale pour le graphe de \(f\).

Si une fonction possède une asymptote verticale, cela signifie qu'il existe au moins une portion de son graphe qui, infiniment loin de l'origine, s'approche de plus en plus de son asymptote:

Si au moins une des limites \(\lim_{x\to \infty}f(x)\), \(\lim_{x\to -\infty}f(x)\), existe et vaut \(L\), on dit que la droite horizontale d'équation \(y=L\) est une asymptote horizontale pour le graphe de \(f\).

Exemple: Étudions les asymptotes de \(\displaystyle f(x)=\frac{1}{x^2+x-2}\), sur \(D_f=\mathbb{R}\setminus\{-2,1\}\).

Puisque \(\displaystyle \lim_{x\to \pm \infty}f(x)=0\), la droite \(y=0\) est asymptote horizontale.
Puisque \(\displaystyle \lim_{x\to -2^{\pm}}f(x)=\mp \infty\), la droite \(x=-2\) est asymptote verticale.
Puisque \(\displaystyle \lim_{x\to 1^{\pm}}f(x)=\pm \infty\), la droite \(x=1\) est asymptote verticale.

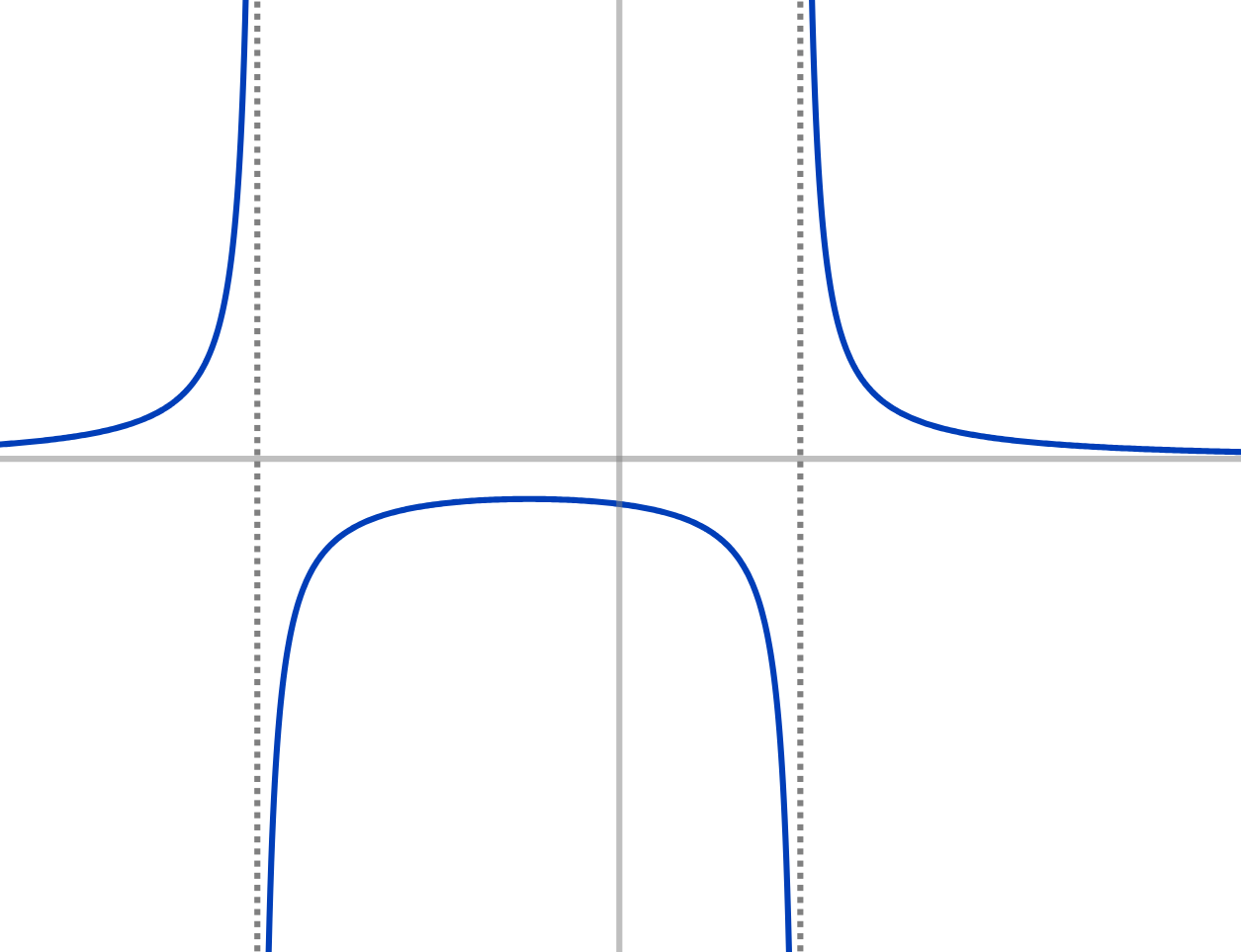
Si \(f(x)\) n'a pas de limite lorsque \(x\to \pm \infty\), c'est qu'il n'y a pas d'asymptote horizontale. Mais cela n'empêche pas que \(f\) possède des portions infiniment loin de l'origine, proches d'une droite oblique (c'est-à-dire de pente non-nulle).

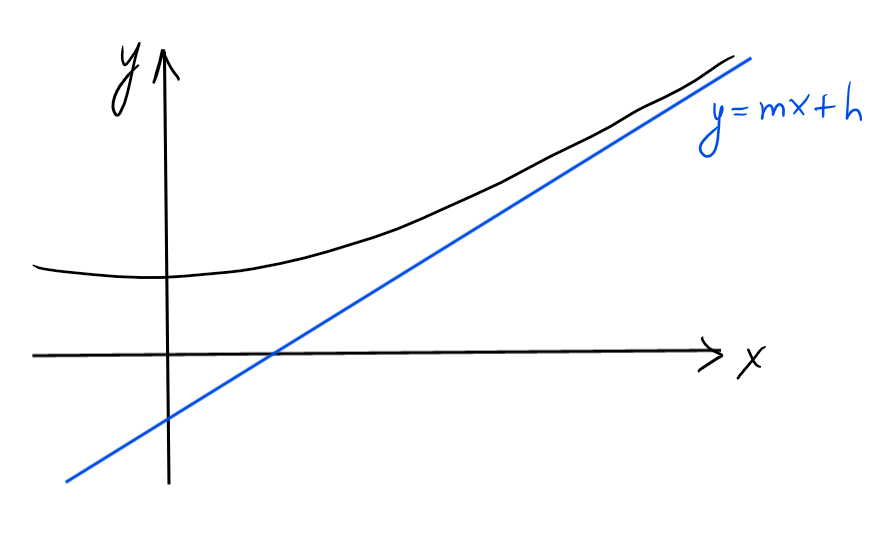
Si \(\lim_{x\to \infty} f(x)=\pm \infty\) et s'il existe \(m,h\in \mathbb{R}\) tels que \(m\neq 0\) et \[\lim_{x\to \infty} |f(x)-(mx+h)|=0,\] la droite d'équation \(y=mx+h\) est une asymptote oblique pour le graphe de \(f\). (On a une définition semblable si \(x\to -\infty\).)

Si on sait que \(y=mx+h\) est asymptote oblique, comment trouver \(m\) et \(h\)?

Remarquons que si on a à la fois \[ \lim_{x\to \infty}f(x)=+\infty\, \quad \text{ et }\quad \lim_{x\to \infty} |f(x)-(mx+h)|=0\,, \] avec \(m\neq 0\), alors la limite \(\lim_{x\to \infty} f(x)-(mx+h)\) représente une indétermination ''\(\infty-\infty\)''. Mais puisque cette limite est nulle, on peut réécrire \[0=\lim_{x\to \infty} |f(x)-(mx+h)| =\lim_{x\to \infty} |x|\cdot\left|\frac{f(x)}{x}-\left(m+\frac{h}{x}\right)\right|\,.\] Puisque \(|x|\to \infty\), on doit donc nécessairement avoir que \[ \lim_{x\to \infty} \left|\frac{f(x)}{x}-\left(m+\frac{h}{x}\right)\right| =0\,. \] Mais comme \(\frac{h}{x}\to 0\), on a \[\lim_{x\to \infty} \left|\frac{f(x)}{x}-m\right|=0\] et donc \[m=\lim_{x\to \infty} \frac{f(x)}{x}\,,\] ce qui fixe la valeur de \(m\).

En connaissant \(m\) on peut alors trouver \(h\), puisque \[ \lim_{x\to \infty} |f(x)-(mx+h)|=0 \quad\Longrightarrow\quad h=\lim_{x\to \infty}(f(x)-mx).\]

Exemple: Étudions les asymptotes du graphe de \(f(x)=\sqrt{x^2+x}\), définie sur \(D_f=[-1,0]\). Remarquons que \[ \lim_{x\to \pm\infty}\sqrt{x^2+x} =\lim_{x\to \pm\infty}|x|\cdot\sqrt{1+\frac{1}{x}} =+\infty\,,\] donc il n'y a pas d'asymptotes horizontales. Pour voir s'il peut y en avoir des obliques, étudions les limites \[\begin{aligned} m =\lim_{x\to \pm\infty} \frac{f(x)}{x} &=\lim_{x\to \pm\infty} \frac{|x|\sqrt{1+\frac{1}{x}}}{x}\\ &=\lim_{x\to \pm\infty} \frac{\pm x\sqrt{1+\frac{1}{x}}}{x}=\pm 1\,. \end{aligned}\] On peut donc passer à \[\begin{aligned} h =\lim_{x\to \pm \infty}(f(x)-(\pm 1)x) &=\lim_{x\to \pm \infty}(\sqrt{x^2+x}\mp x)\\ &=\lim_{x\to \pm \infty}\frac{x}{\sqrt{x^2+x}\pm x}\\ &=\lim_{x\to \pm \infty}\frac{x}{\pm x\sqrt{1+\frac{1}{x}}\pm 1}\\ &=\pm \frac{1}{2}. \end{aligned}\] On a donc l'asymptote oblique \(y=x+\frac{1}{2}\) lorsque \(x\to +\infty\) et l'asymptote oblique \(y=-x-\frac{1}{2}\) lorsque \(x\to -\infty\).

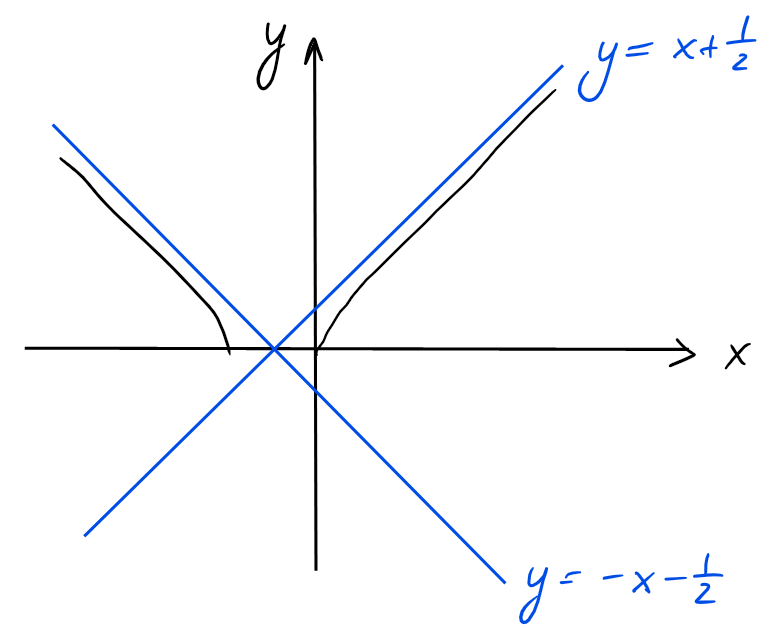
La procédure présentée ci-dessus a montré que l'existence d'une asymptote oblique \(y=mx+h\) procède comme suit: on trouve la pente \(m\) (si la limite qui la définit existe), et ensuite on trouve l'ordonnée à l'origine \(h\), si la limite qui la définit existe.

Or il se pourrait très bien que \(m\) existe mais que \(f(x)-mx\) n'ait pas de limite.

Exemple: Si \(f(x)=x+\sin(x)\), alors \[\begin{aligned} m =\lim_{x\to+\infty}\frac{f(x)}{x} &=\lim_{x\to+\infty}\frac{x+\sin(x)}{x}\\ &=1+\lim_{x\to+\infty}\frac{\sin(x)}{x} =1\,, \end{aligned}\] mais \(h\) n'existe pas puisque \(f(x)-1x=\sin(x)\), qui n'a pas de limite lorsque \(x\to \infty\). Donc il n'existe aucune droite \(y=x+h\) telle que \[ \lim_{x\to+\infty}|f(x)-(x+h)|=0\,, \] donc il n'y a pas d'asymptote oblique pour le graphe de \(f\).

Que se passe-t-il, alors, dans le cas où la limite qui définit \(h\) est infinie?

Si \(\displaystyle m=\lim_{x\to+\infty}\frac{f(x)}{x}\) existe mais \[ \lim_{x\to +\infty}(f(x)-mx)=\pm \infty\,, \] on dit que \(f\) admet une branche parabolique (de direction de pente \(m\)). (On a une définition semblable si \(x\to -\infty\).)

Expliquons le pourquoi de cette terminologie sur un exemple.

Exemple: Considérons \(f(x)=\sqrt{x}\), sur \(\mathbb{R}_+\). On a que \[\lim_{x\to+\infty}\sqrt{x}=+\infty \,, \] et \[\begin{aligned} m =\lim_{x\to+\infty}\frac{f(x)}{x} &=\lim_{x\to+\infty}\frac{\sqrt{x}}{x}\\ &=\lim_{x\to+\infty}\frac{1}{\sqrt{x}} =0\,, \end{aligned}\] alors que \[ \lim_{x\to+\infty}(f(x)-0x) = \lim_{x\to+\infty}\sqrt{x} = \infty\,, \] donc le graphe de \(f\) possède une branche parabolique de direction horizontale \(m=0\). (Sans pour autant posséder d'asymptote horizontale!)

Dans certains cas où \(m\) n'existe pas, on peut quand-même avoir une information sur le comportement de la fonction loin de l'origine:

(Le cas ''\(m=\pm\infty\)''.) Si \[ \lim_{x\to +\infty}\frac{f(x)}{x}=\pm\infty\,, \] on dit que \(f\) admet une branche parabolique de direction verticale. (On a une définition semblable si \(x\to -\infty\).)

Exemple: Si \(f(x)=x^2-3x\), alors \[ \lim_{x\to\pm \infty}\frac{f(x)}{x}= \lim_{x\to\pm \infty}\frac{x^2-3x}{x}= \lim_{x\to\pm \infty}(x-3)= \pm\infty\,, \] donc le graphe de \(f\) possède une branche parabolique verticale.

Elements de l'étude d'une fonction

Regroupons maintenant certaines des étapes que l'on pourra, lorsque c'est possible, inclure dans l'étude d'une fonction réelle \(f\) définie sur son domaine \(D_f\).

Si \(D_f\) est symétrique (\(x\in D_f\Leftrightarrow -x\in D_f\)), il sera utile de tester la parité de \(f\). Cas échéant, cette parité devra se retrouver plus tard dans la représentation graphique de \(f\).
Lorsque c'est possible, l'étude du signe de \(f\) pourra aussi renseigner sur la position du graphe de \(f\) relativement à \(Ox\).
La recherche des points de continuité/discontinuité de \(f\).
Sur les parties de de \(D_f\) où \(f\) est dérivable, l'analyse du signe de \(f'\) renseignera sur la variation de \(f\), et mènera dans certains cas à la détermination des extrema locaux de \(f\). Lorsqu'il y en a, on pourra déterminer les extrema globaux de \(f\).
Si \(D_f\) le permet et s'il y en a, étudier la nature des branches infinies de \(f\) (asymptotes horizontales, verticales, obliques ou paraboliques).
Enfin, tracer un graphe contenant les principales informations obtenues dans l'étude analytique.

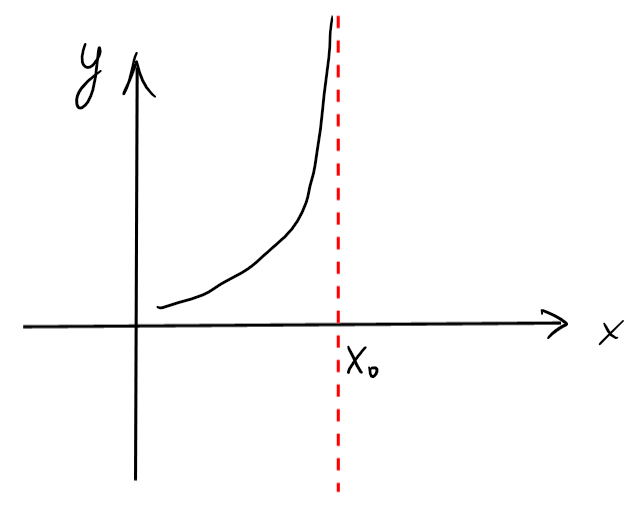
Remarquons qu'une fonction peut présenter un comportement intéressant proche de certains points. Par exemple, lorsque \(f\) est dérivable dans un voisinage épointé de \(x_0\), on dira que \(f\) possède

un point de tangence verticale en \(x_0\) si \(\lim_{x\to x_0}f'(x)=+ \infty\) ou \(-\infty\),
un point anguleux en \(x_0\) si \(\lim_{x\to x_0^-}f'(x)\) et \(\lim_{x\to x_0^+}f'(x)\) existent et sont distinctes,
un point de rebroussement en \(x_0\) si \[ \lim_{x\to x_0^-}f'(x)=-\infty \qquad \text{ et }\qquad \lim_{x\to x_0^+}f'(x)=+\infty\,, \] ou \[ \lim_{x\to x_0^-}f'(x)=+\infty \qquad \text{ et }\qquad \lim_{x\to x_0^+}f'(x)=-\infty\,, \]
Si la fonction est continue en ces points, ils correspondent donc à des extrema locaux.

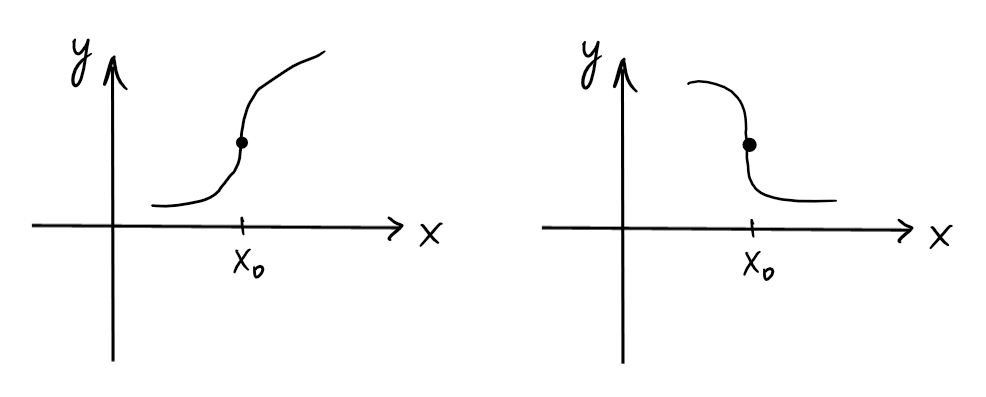
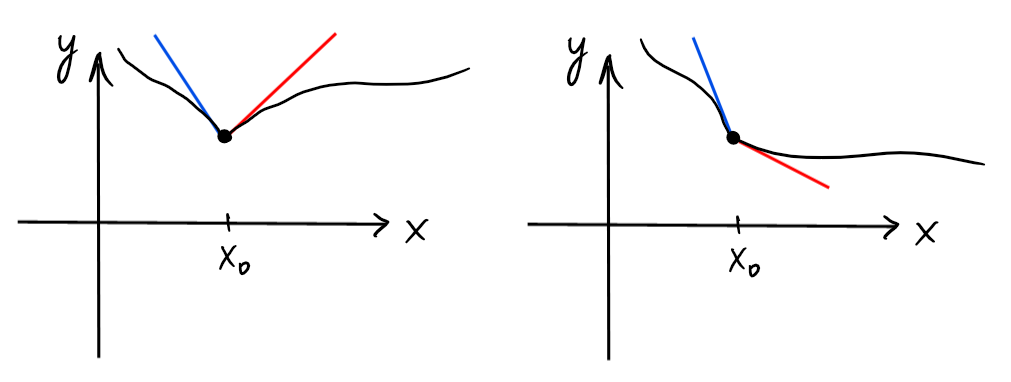
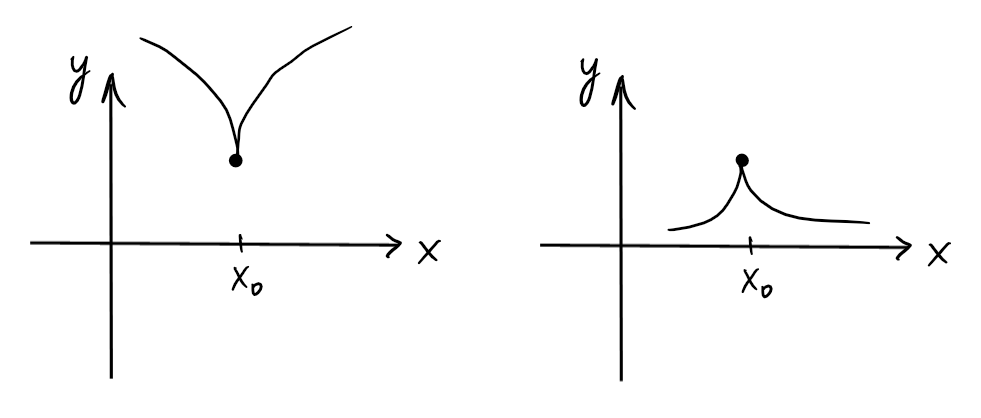
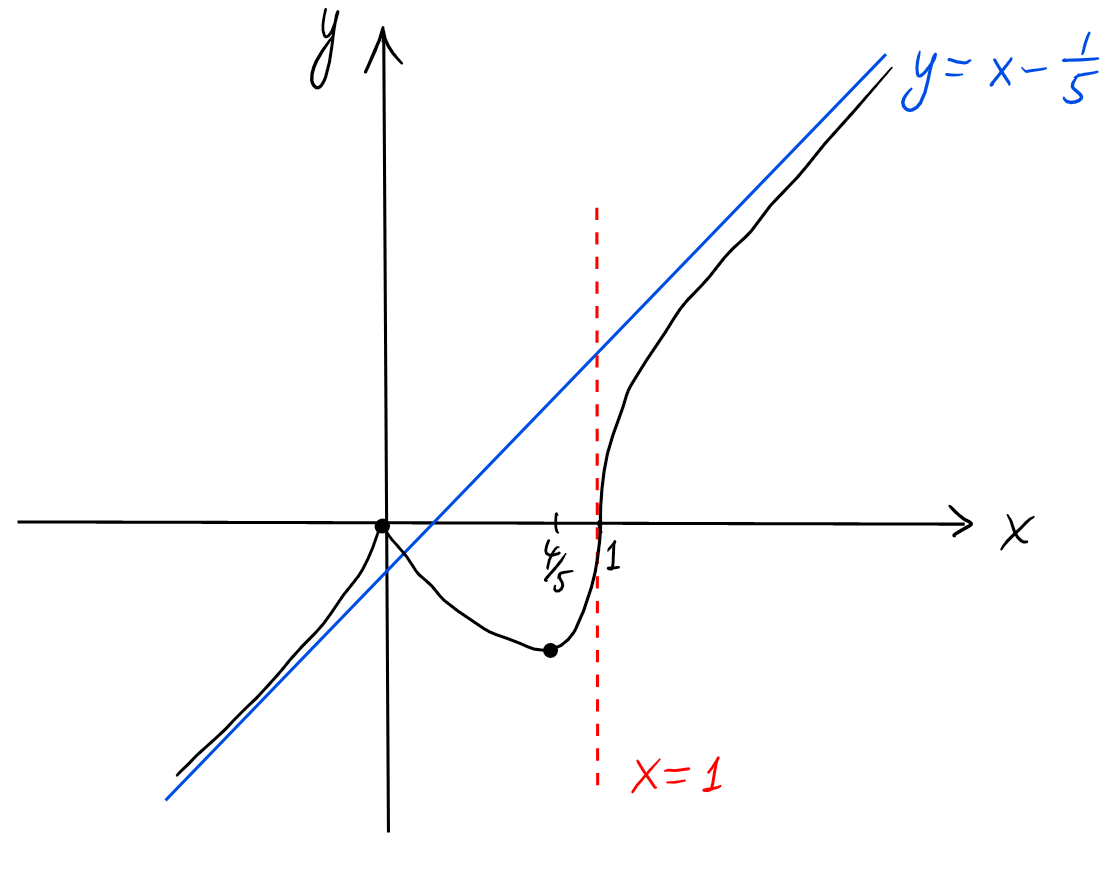
Exemple: Sur \(D_f=\mathbb{R}\), étudions \[ f(x)=\sqrt[5]{x^4(x-1)} \] Le signe de \(f\) est régi par celui de \(x-1\):

Étant un produit de fonctions continues, \(f\) est continue sur \(\mathbb{R}\). Calculons ensuite \[ f'(x) =\left((x^4(x-1))^{1/5}\right)' =\frac{5x-4}{5\sqrt[5]{x}\sqrt[5]{(x-1)^4}}\,. \] Ainsi, \(f\) n'est pas dérivable en \(x=0\) et en \(x=1\), et \(f'(\frac45)=0\).

Donc \(f\) possède un minimum local en \(x=\frac45\), au point \((\frac45,f(\frac45))\).

Remarquons aussi que

\(\lim_{x\to 0^{\mp}}f'(x)=\pm\infty\), donc \(f\) possède un point de rebroussement en \(x=0\), qui implique que \((0,0)\) est un maximum local
\(\lim_{x\to 1}f'(x)=+\infty\), donc \(f\) possède un point de tangence verticale en \(x=1\).

Passons à l'étude des branches infinies. Pour commencer, \[\begin{aligned} \lim_{x\to \pm \infty} f(x) =\lim_{x\to \pm \infty}\sqrt[5]{x^5\left(1-\frac{1}{x}\right)} =\lim_{x\to \pm \infty}x\sqrt[5]{1-\frac{1}{x}} =\pm \infty\,, \end{aligned}\] ce qui implique que \(f\) ne possède pas d'extrema globaux.

Ensuite, \[ m =\lim_{x\to \pm \infty} \frac{f(x)}{x} =\lim_{x\to \pm \infty} \sqrt[5]{1-\frac{1}{x}} =1\,, \] et \[ h =\lim_{x\to \pm \infty} (f(x)-(1)x) =\lim_{x\to \pm \infty} \left[\sqrt[5]{x^4(x-1)}-x\right]. \] En posant \(a=\sqrt[5]{x^4(x-1)}\) et \(b=x\), on peut utiliser \[a^5-b^5=(a-b)(a^4+a^3b+a^2b^2+ab^3+b^4).\] Ainsi, on obtient \[\begin{aligned} \lim_{x\to \pm \infty}& \left[\sqrt[5]{x^4(x-1)}-x\right]\\ &= \lim_{x\to \pm \infty}(a-b)\\ &=\lim_{x\to \pm \infty}\frac{a^5-b^5}{a^4+a^3b+a^2b^2+ab^3+b^4}\\ &=\lim_{x\to \pm \infty}\frac{x^4(x-1)-x^5}{a^4+a^3b+a^2b^2+ab^3+b^4}\\ &=\lim_{x\to \pm \infty}\frac{-1}{\left(1-\frac{1}{x}\right)^{\frac{4}{5}}+\left(1-\frac{1}{x}\right)^{\frac{3}{5}}+\left(1-\frac{1}{x}\right)^{\frac{2}{5}}+\left(1-\frac{1}{x}\right)^{\frac{1}{5}}+1}\\ &=-\frac{1}{5}. \end{aligned}\] On a donc l'asymptote oblique \(y=x-\frac{1}{5}\) lorsque \(x\to \pm \infty\).

On peut maintenant tracer le graphe de \(f\):