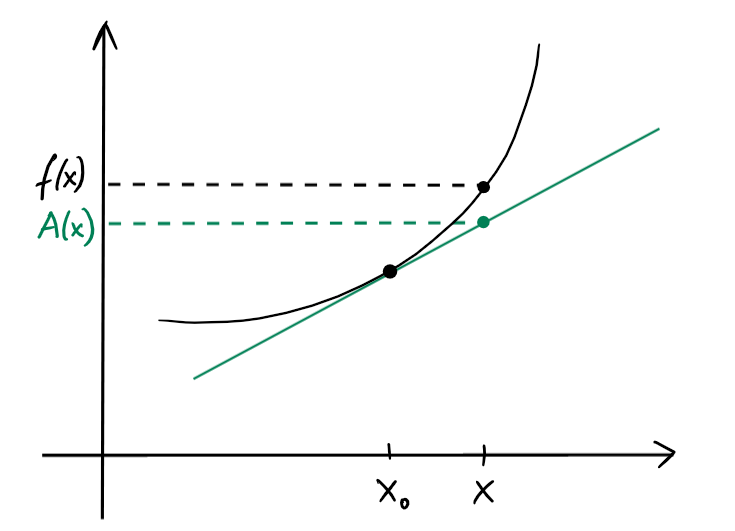
Considérons une fonction \(f\) dérivable en \(x_0\), ainsi que la droite tangente au graphe de \(f\) au point \((x_0,f(x_0))\): \[y=f(x_0)+f'(x_0)(x-x_0)\,,\] Pour souligner la dépendance en \(x\), écrivons \(y=A(x)\), où \[ A(x)=f(x_0)+f'(x_0)(x-x_0) \]
Le nombre \(A(x)\) approxime bien la valeur de \(f(x)\)
au voisinage de \(x_0\), dans le sens suivant.
Commençons par exprimer la différence
\[\begin{aligned}
f(x)-A(x)&=f(x)-[f'(x_0)(x-x_0)+f(x_0)]\\
&=(x-x_0)\cdot \left[\frac{f(x)-f(x_0)}{x-x_0}-f'(x_0)\right]\,,
\end{aligned}\]
où l'on voit apparaître la différence entre le rapport de Newton et
\(f'(x_0)\), qui tend vers \(0\) lorsque \(x\to x_0\) puisque \(f\) est
dérivable en \(x_0\).
Ainsi, \(f(x)-A(x)\) est un produit de deux termes qui tendent vers zéro.
On appelle \(A(x)\) l'approximation linéaire de \(f(x)\) au voisinage
\(x_0\).
Exemple: L'approximation linéaire de \(f(x)=\sin(x)\) au voisinage de \(x_0=0\) est donnée par \[\begin{aligned} A(x)& =f(0)+f'(0)(x-0)\\ &=\sin(0)+\sin'(0)(x-0)\\ &=x \end{aligned}\]
Exemple: L'approximation linéaire de \(f(x)=\sqrt[3]{x}\) au voisinage de \(x_0=8\) est donnée par \[\begin{aligned} A(x) &=f(8)+f'(8)(x-8)\\ &=\sqrt[3]{8}+\tfrac13 8^{-2/3}(x-8)\\ &=2+\tfrac{1}{12}(x-8)\,. \end{aligned}\] Par exemple, avec \(x=8.012\), on approxime \(\sqrt[3]{8.012}=f(8.012)\) par \[ A(8.012)=2+\tfrac{1}{12}(8.012-8)=2.001 \] Remarquons que la ''vraie'' valeur est \(f(8.012) =\sqrt[3]{8.012}=2.00099949\ldots\)
Dernière compilation: 2024-06-03 (22:36:08)
Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)
