L'équation de la sécante \(d\) passant par \((a,f(a))\) et \((b,f(b))\) est \[y=\left(\frac{f(b)-f(a)}{b-a}\right)\cdot (x-a)+f(a).\]
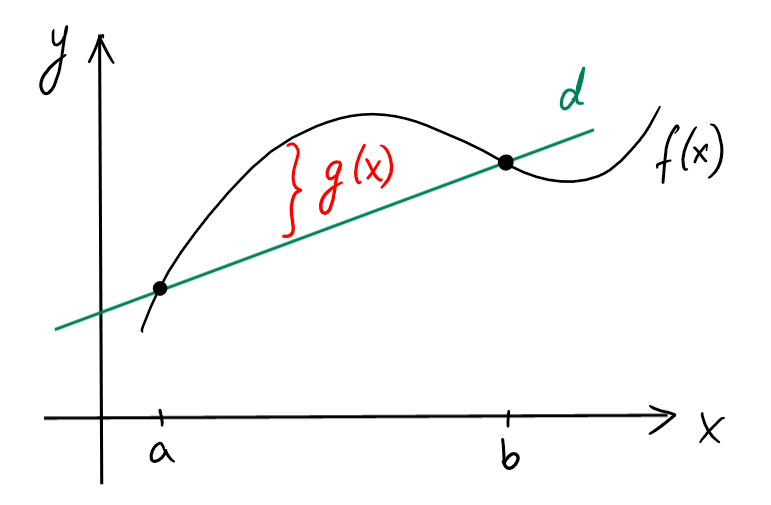
Théorème:[Théorème des accroissements finis (TAF)] Soit \(f\) continue sur \([a,b]\) et dérivable sur \(]a,b[\). Alors il existe \(x_0\in ]a,b[\) tel que \[ f'(x_0)=\frac{f(b)-f(a)}{b-a}\,. \]
L'équation de la sécante \(d\) passant par \((a,f(a))\) et \((b,f(b))\) est \[y=\left(\frac{f(b)-f(a)}{b-a}\right)\cdot (x-a)+f(a).\]

Remarques:
Exemples:
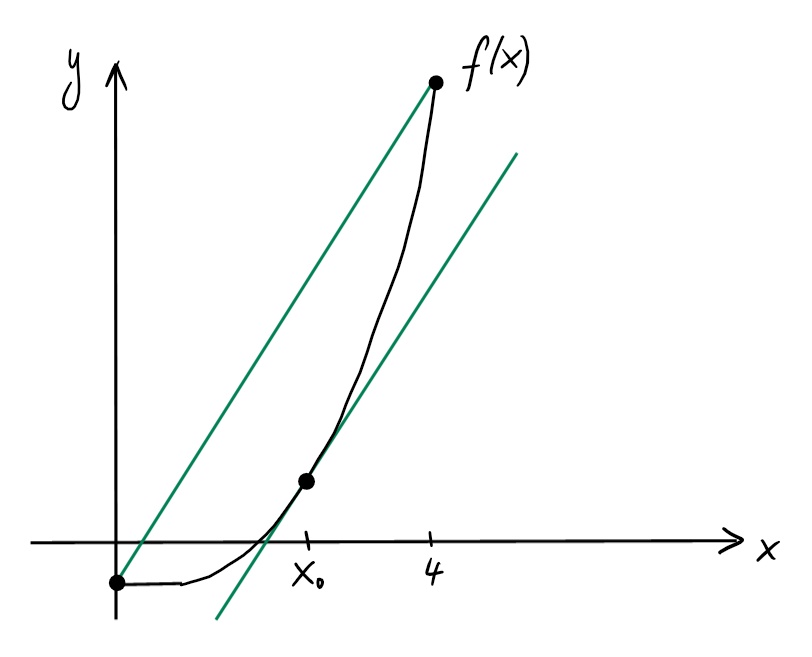
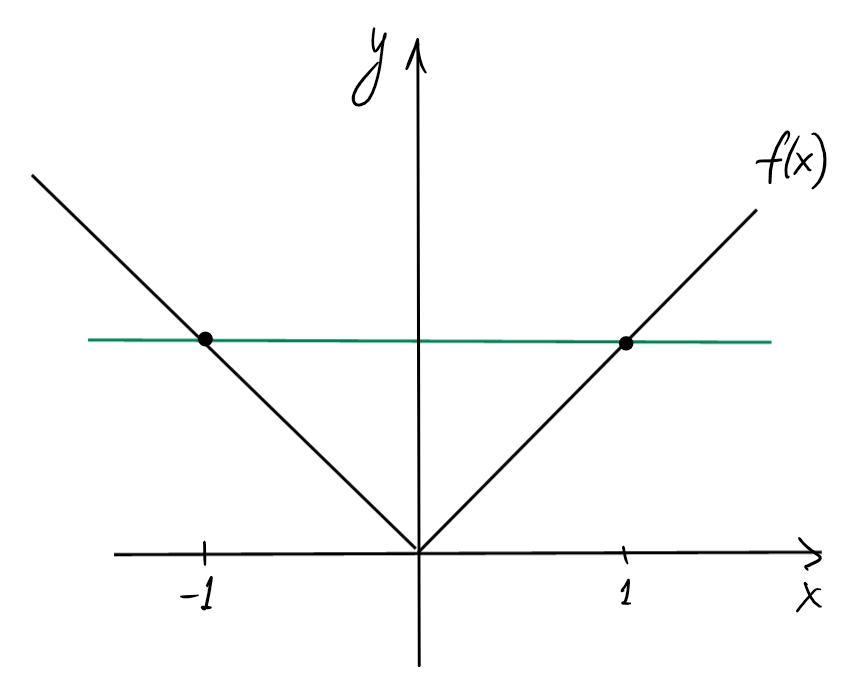
On va maintenant parler de quelques conséquences du TAF. Comme on a mentionné, ce résultat nous aide à déduire des conséquences géométriques de la dérivée. Si on a des informations sur \(f\), on peut pendre la limite du rapport du Newton pour trouver \(f'\) et déduire des informations sur la variation de la fonction. Mais si on a des informations sur la dérivée, comment avoir de l'information sur \(f\) ? On ne peut pas ''défaire'' la limite, mais on peut justement utiliser le TAF.
On sait que pour une fonction constante, la dérivée s'annule. Le TAF nous permet de montrer que l'implication inverse est vraie aussi.
Pour n'importe quels \(a,b \in I\) avec \(a\lt b\), il existe \(x_0\in ]a,b[\) tel que \(f'(x_0)=\frac{f(b)-f(a)}{b-a}\) par le TAF. Or \(f'(x_0)=0\), donc \(\frac{f(b)-f(a)}{b-a}=0\) et alors \(f(b)=f(a)\). Comme ceci est vrai pour n'importe quels \(a,b\in I\), \(f\) prend donc la même valeur partout sur \(I\), donc \(f(x)=c\) pour une certaine constante \(c\in\mathbb{R}\).
Laissée en exercice.
On montre la première équivalence, la deuxième est laissée en exercice.
Supposons d'abord que \(f\) est croissante sur \(I\). Prenons \(x_0\in I\) et
\(h\gt 0\) tel que \(x_0+h\in I\). Alors on a \(f(x_0+h)\geqslant f(x_0)\), et donc
\(\frac{f(x_0+h)-f(x_0)}{h}\geqslant 0\), d'où
\[f'_+(x_0)=\lim_{h\to 0^+}\frac{f(x_0+h)-f(x_0)}{h}\geqslant 0.\]
Mais puisque \(f\) est dérivable en \(x_0\), \(f'(x_0)=f'_+(x_0)\), et donc on a
\(f'(x_0)\geqslant 0\).
Supposons maintenant que \(f'(x)\geqslant 0\) pour tout \(x\in I\). Soient \(a,b\in
I\) tels que \(a\lt b\). Par le TAF appliqué à l'intervalle \([a,b]\), il existe
\(c\in ]a,b[\) tel ue
\[\frac{f(b)-f(a)}{b-a}=f'(c)\geqslant 0.\]
Puisque \(b-a\gt 0\), on a donc que \(f(b)-f(a)\geqslant 0\), d'où \(f(a)\leqslant f(b)\).
On remarque qu'on a aussi
Par contre, une fonction strictement croissante ou strictement décroissante peut avoir une dérivée nulle, par exemple \(f(x)=x^3\) en \(0\).
La fonction \(f\) est continue en \(x_0\) et dérivable sur un voisinage épointé de \(x_0\). Donc pour tout \(h\) tel que \(x_0+h\) appartient à ce voisinage, on peut appliquer le TAF sur l'intervalle \([x_0,x_0+h]\) si \(h\gt 0\), ou \([x_0+h,x_0]\) si \(h\lt 0\): \[\exists t\in ]0,1[ \ \text{ tel que } \ \frac{f(x_0+h)-f(x_0)}{h}=f'(x_0+t\cdot h).\] Lorsque \(h \to 0\), \[\lim_{h\to 0}\frac{f(x_0+h)-f(x_0)}{h}=\lim_{h\to 0}f'(x_0+t\cdot h).\] Par hypothèse, la limite \(\lim_{x\to x_0}f'(x)\) existe. Elle est donc unique et ne dépend pas de la façon dont \(x\) tend vers \(x_0\). On a alors \[\lim_{x\to x_0}f'(x)=\lim_{h\to 0}f'(x_0+t\cdot h).\] Alors \(f'(x_0)\) existe et \[f'(x_0)=\lim_{h\to 0} \frac{f(x_0+h)-f(x_0)}{h}=\lim_{h\to 0}f'(x_0+t\cdot h)=\lim_{x \to x_0} f'(x).\]
Attention: ce résultat ne dit pas que la dérivée est continue ! Il dit juste que
la seule façon de ne pas être continue pour une fonction dérivée est une limite
\(\lim_{x\rightarrow x_0} f'(x)\) non existante.
Ce corollaire est utile si par exemple on a une fonction qui est clairement
dérivable à gauche et à droite de \(x_0\), et on voudrait montrer qu'elle l'est
aussi en \(x_0\). Au lieu de calculer et comparer les dérivées à gauche et à
droite, grâce à ce corollaire, on peut simplement montrer que \(\lim_{x\to x_0}
f'(x)\) existe (en calculant cette limite à gauche et à droite, par exemple) et
ainsi on aura que \(f'(x_0)=\lim_{x\rightarrow x_0} f'(x)\).
Exemple: Soit \(f(x)= \begin{cases} -1 & \text{ si } x\leqslant 1,\\ x^2-2x & \text{ si } x\gt 1. \end{cases}\) On peut montrer que \(f\) est dérivable en \(1\) en calculant \[\begin{aligned} &\lim_{h\to 0^-} \frac{f(1+h)-f(1)}{h}=\lim_{h\to 0^-}\frac{-1-(-1)}{h}=0,\\ &\lim_{h\to 0^+} \frac{f(1+h)-f(1)}{h}=\lim_{h\to 0^+}\frac{(1+h)^2-2(1+h)-(-1)}{h} =\lim_{h\to 0^+}\frac{h^2}{h}=0. \end{aligned}\] Mais grâce au corollaire ci-dessus, on peut simplement constater que \(f\) est continue, on a \[f'(x)= \begin{cases} 0 & \text{ si } x\lt 1,\\ 2x-2 & \text{ si } x\gt 1, \end{cases}\] et \(\lim_{x\to 1} f'(x)\) existe et vaut \(0\). On a donc que \(f'(1)=0\).
Le théorème suivant sera utilisé dans la preuve de la Règle de Bernoulli--de l'Hôpital.
Théorème:[TAF généralisé] Soient \(f\) et \(g\) continues sur \([a,b]\) et dérivables sur \(]a,b[\), tel que \(g'(x)\neq 0\) pour tout \(x\in]a,b[\). Alors il existe \(t\in ]a,b[\) tel que \[\frac{f'(t)}{g'(t)}=\frac{f(b)-f(a)}{g(b)-g(a)}.\]
Idée: On applique le TAF à la fonction \(h(x):=(f(b)-f(a))g(x)-(g(b)-g(a))f(x)\).
On remarque qu'en prenant \(g(x)=x\), on retrouve le TAF.