Analyse B (MAN)

Une fonction \(f:[a,b]\to\mathbb{R}\) possède

un maximum global en \(x_0\) si pour tout \(x\in [a,b]\), on a \(f(x)\leqslant f(x_0)\); on dit alors que son maximum est atteint en \(x_0\).
un minimum global en \(x_0\) si pour tout \(x\in [a,b]\), on a \(f(x)\geqslant f(x_0)\); on dit alors que son minimum est atteint en \(x_0\)..

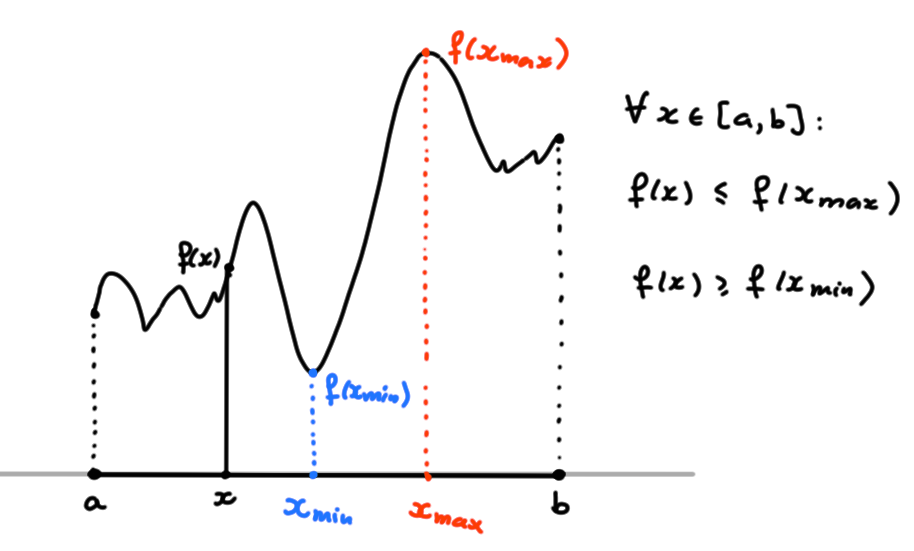
Théorème: Soit \(f:[a,b]\to\mathbb{R}\) continue. Alors \(f\) atteint son maximum et son minimum sur \([a,b]\).

Combiné avec le Théorème des valeurs intermédiaires, ce résultat implique que l'image d'un intervalle fermé et borné, par une fonction continue, est aussi un intervalle fermé et borné.

La recherche des max/min globaux peut parfois se faire à l'aide de l'étude de la dérivée de la fonction, lorsque celle-ci existe. Mais puisque la dérivée est une propriété locale des fonctions, on a aussi besoin d'une notion local de max/min.

Une fonction \(f\) possède

un maximum local en \(x_0\) si il existe un voisinage de \(x_0\) sur lequel \(f(x)\leqslant f(x_0)\)
un minimum local en \(x_0\) si il existe un voisinage de \(x_0\) sur lequel \(f(x)\geqslant f(x_0)\)

Théorème: Soit \(f\) dérivable sur \(]a,b[\). Si \(f\) possède un minimum ou maximum local en \(x_0\in ]a,b[\), alors \(f'(x_0)=0\).

Preuve:

Supposons que \(f\) admet un maximum local en \(x_0\in ]a,b[\) (on a une preuve analogue dans le cas d'un minimum). Puisque \(f\) est dérivable en \(x_0\), elle est en particulier à gauche et à droite en \(x_0\), ce qui implique \[\begin{aligned} f'(x_0) &=\lim_{h\to 0^+}\frac{f(x_0+h)-f(x_0)}{h}\\ &=\lim_{h\to 0^-}\frac{f(x_0+h)-f(x_0)}{h}\,. \end{aligned}\] Mais, puisque \(f(x_0)\) est un maximum local, on a \(f(x_0+h)\leqslant f(x_0)\) pour tout \(h\) suffisamment petit. On a donc d'une part que \[\lim_{h\to 0^+}\frac{f(x_0+h)-f(x_0)}{h}\leqslant 0\,, \] et d'autre part que \[ \lim_{h\to 0^-}\frac{f(x_0+h)-f(x_0)}{h}\geqslant 0\,. \] Ceci implique que \(0\leqslant f'(x_0)\leqslant 0\), d'où \(f'(x_0)=0\).

Remarquons que l'implication inverse n'est pas vraie. Par exemple, la dérivée de la fonction \(f(x)=x^3\) s'annule en \(0\) mais la fonction n'y possède pas de maximum ni de minimum.

Théorème: [Théorème de Rolle] Soit \(f\) continue sur \([a,b]\) et dérivable sur \(]a,b[\). Si \(f(a)=f(b)\), alors il existe \(x_0\in ]a,b[\) tel que \(f'(x_0)=0\).

Preuve:

Comme \(f\) y est continue, \(f\) atteint son maximum et son minimum global sur \([a,b]\).

Si un maximum ou un minimum se trouve en un point intérieur \(x_0\in]a,b[\), alors par le résultat précédent, on a \(f'(x_0)=0\).
Si il n'y a pas de maximum ou de minimum en un point intérieur, alors la valeur \(f(a)=f(b)\) est à la fois le maximum et le minimum de \(f\) sur \([a,b]\). Ceci implique que \(f\) est constante sur \([a,b]\) et donc \(f'(x)=0\) pour tout \(x\in ]a,b[\).

5.5 Théorème de Rolle