6.2 Vecteur tangent

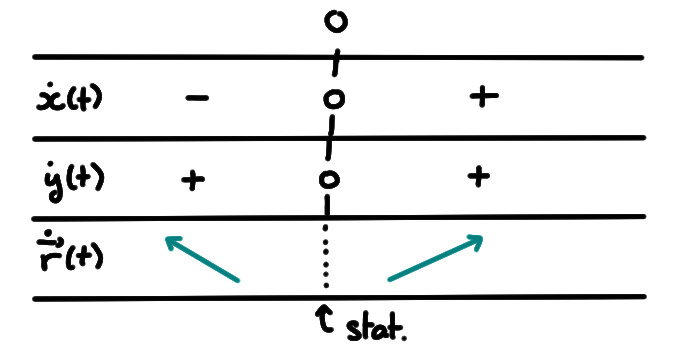
L'utilisation du rayon-vecteur permet de comparer les positions en deux instants \(t_0\lt t_0+\Delta t\), à l'aide du déplacement \(\vec{r}(t_0+\Delta t )-\vec{r}(t_0)\):

On s'attend à ce que si les instants \(t_0\) et \(t_0+\Delta t \) sont très rapprochés, le déplacement devienne aussi petit. Si on divise ce vecteur par la durée de l'intervalle \([t_0,t_0+\Delta t ]\), le quotient \[ \frac{\vec{r}(t_0+\Delta t )-\vec{r}(t_0)}{\Delta t } \] doit être interprété comme une vitesse sur cet intervalle.

Dans la limite où \(\Delta t \to 0\), on fait ainsi apparaître les dérivées des fonctions \(x(t)\) et \(y(t)\) par rapport au temps: \[ \lim_{\Delta t \to 0}\frac{\vec{r}(t_0+\Delta t )-\vec{r}(t_0)}{\Delta t }= \begin{pmatrix} \displaystyle\lim_{\Delta t \to 0}\frac{x(t_0+\Delta t )-x(t_0)}{\Delta t }\\ \\ \displaystyle\lim_{\Delta t \to 0}\frac{y(t_0+\Delta t )-y(t_0)}{\Delta t }\\ \end{pmatrix}= \begin{pmatrix} \dot{x}(t_0)\\ \dot{y}(t_0) \end{pmatrix}\, \]

Remarque: Dans ce chapitre, on utilise le ''point'' \(\dot{x}\) au lieu du ''prime'' \(x'\). C'est une convention souvent adoptée dans les ouvrages traitant de cinématique, où le ''point'' indique une dérivée par rapport au temps.

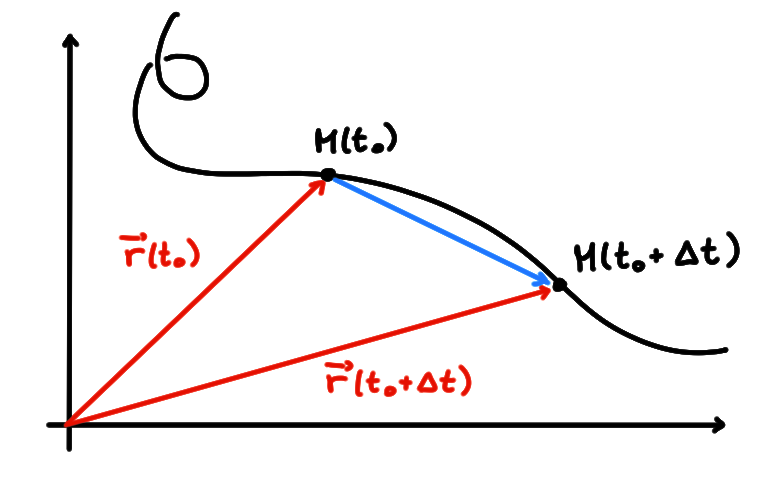
Lorsque \(x(t_0)\) et \(y(t_0)\) sont dérivables au temps \(t_0\), le vecteur \[ \dot{\vec{r}}(t_0) := \begin{pmatrix} \dot{x}(t_0)\\ \dot{y}(t_0) \end{pmatrix}\, \] est appelé le vecteur tangent de la courbe paramétrée \(M\) au temps \(t_0\).

S'il ne s'annule pas, le vecteur tangent donne en particulier la direction de la tangente à la courbe en au point \(M(t_0)\):

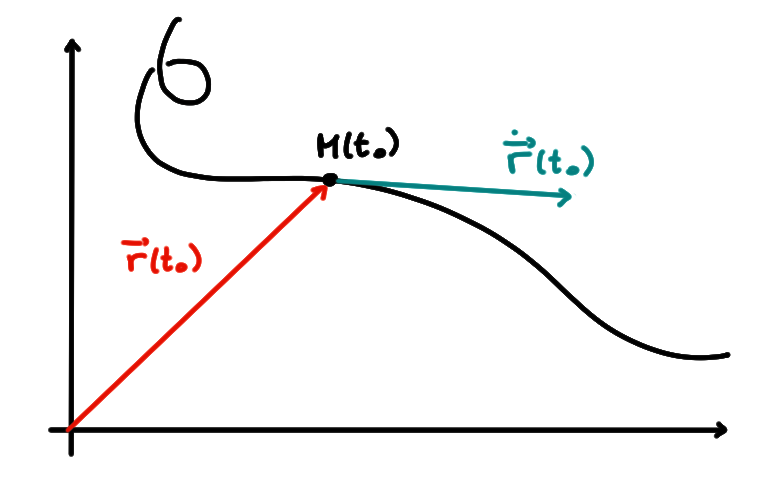
Mais il donne plus d'informations que ça, puisqu'il doit être interprété comme le vecteur de vitesse instantanée de la particule à l'instant \(t_0\); il donne aussi le sens du déplacement.

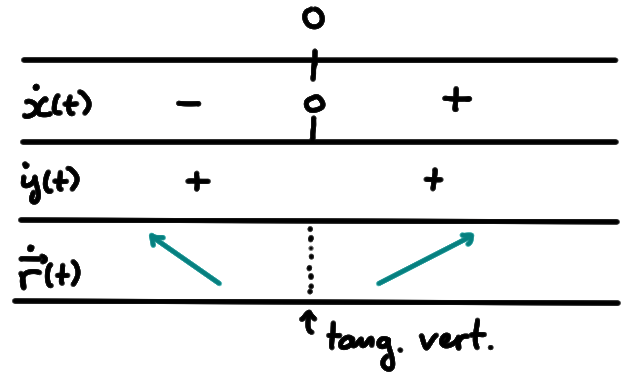
L'étude des signes de \(\dot{x}(t)\) et \(\dot{y}(t)\) renseigne donc sur la direction et le sens de déplacement de la particule à l'instant \(t\):

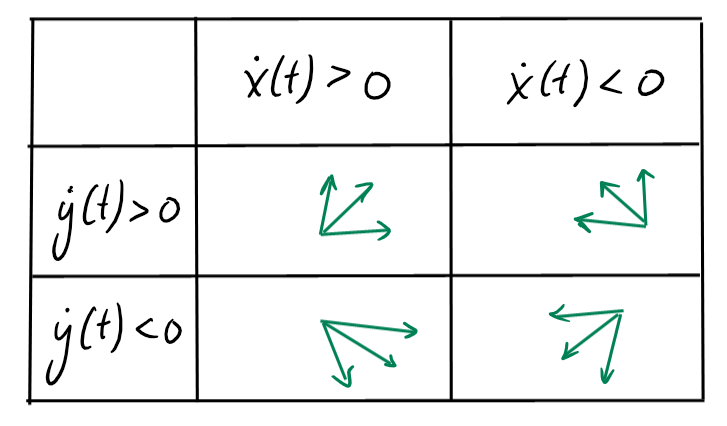
En particulier,

Exemple: Considérons la courbe \[\begin{aligned} M:\mathbb{R}&\longrightarrow \mathbb{R}^2\\ t &\longmapsto M(t) =\left( t^2, t \right)\,. \end{aligned}\] L'étude des signes de \(x(t)=t^2\) et \(y(t)=t\) nous dit déjà à quel quadrant appartient \(M(t)\), en fonction du temps \(t\):

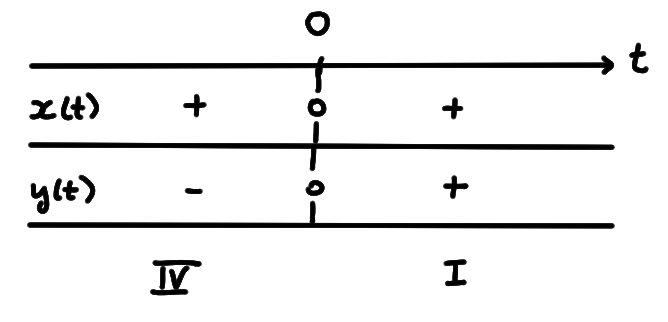
Ensuite, \[\vec{r}(t)= \begin{pmatrix} t^2\\t \end{pmatrix}\,, \qquad \dot{\vec{r}}(t)= \begin{pmatrix} 2t\\1 \end{pmatrix}\,. \] Les signes de \(\dot{x}(t)\) et \(\dot{y}(t)\) donnent la direction dans laquelle pointe \(\dot{\vec{r}}(t)\):
Le point \(M(0)=(0,0)\) est un point de tangence verticale puisque \[ \dot{\vec{r}}(0)= \begin{pmatrix} 0\\1 \end{pmatrix}\,. \] On peut maintenant tracer la courbe:

Exemple: Si on reprend la courbe paramétrée décrivant un cercle, on a \[\vec{r}(t)= \begin{pmatrix} \cos(t)\\ \sin(t) \end{pmatrix}\,, \qquad \dot{\vec{r}}(t)= \begin{pmatrix} -\sin(t)\\ \cos(t) \end{pmatrix}\,. \]

(On remarque que \(\vec{r}(t)\ \bot \ \dot{\vec{r}}(t)\) pour tout \(t\), une caractéristique spécifique au mouvement circulaire.)

Points stationnaires

Considérons un cas où le vecteur tangent peut s'annuler.

Exemple: Pour \(t\in \mathbb{R}\), considérons la courbe décrite par \[ \vec{r}(t)= \begin{pmatrix} t^3\\ t^6/2 \end{pmatrix}\,, \qquad \dot{\vec{r}}(t)= \begin{pmatrix} 3t^2\\ 3t^5 \end{pmatrix}\,. \] Puisque \[ \dot{\vec{r}}(0)= \begin{pmatrix} 0\\ 0 \end{pmatrix}\,, \] le vecteur tangent à l'instant \(t=0\) ne donne aucune information sur l'allure de la courbe au voisinage de ce point (tangence, sens de déplacement, etc.). Comment faire, donc, pour étudier la courbe au voisinage de \(M(0)=(0,0)\)? Ce qu'il faut remarquer c'est que \(t=0\) est l'unique instant où \(\dot{\vec{r}}(t)\) s'annule. Or tant qu'il n'est pas nul, même très petit, il contient quand même de l'information.

On peut par exemple considérer la pente du vecteur tangent en un temps \(t\neq 0\), donnée par \[ \frac{\dot{y}(t)}{\dot{x}(t)}= \frac{3t^5}{3t^2}=t^3\,. \] Au voisinage de \(t=0\), le vecteur tangent a donc une pente qui est négative si \(t\lt 0\), positive si \(t\gt 0\), et dans la limite \(t\to 0\) tend vers \[ \lim_{t\to 0} \frac{\dot{y}(t)}{\dot{x}(t)}= \lim_{t\to 0}t^3=0\,. \] Ceci signifie que la courbe doit possèder en \(t=0\) une tangente horizontale.

Remarquons qu'on aurait pu obtenir la même information en remarquant que \(t^6=(t^3)^2\), et donc \(y(t)=x(t)^2/2\), ce qui signifie que tous les points \(M(t)=(x(t),y(t))\) de la courbe sont sur la parabole \(y=x^2/2\). En particulier, le point \(M(0)=(0,0)\) est forcément un point de tangence horizontale.

\(M(t_0)\) est un point stationnaire de \(\Gamma\) si \(\dot{\vec{r}}(t_0)= \begin{pmatrix} 0\\ 0 \end{pmatrix}\).

Pour étudier \(\Gamma\) au voisinage d'un point stationnaire, on pourra procéder comme dans l'exemple précédent:

Exemple: Considérons, pour \(t\in\mathbb{R}\), la courbe \[ \vec{r}(t)= \begin{pmatrix} t^2\\ t^3 \end{pmatrix}\,, \qquad \dot{\vec{r}}(t)= \begin{pmatrix} 2t\\ 3t^2 \end{pmatrix}\,. \] Puisque \(\dot{\vec{r}}(0)= \begin{pmatrix} 0\\ 0 \end{pmatrix}\), \(M(0)=(0,0)\) est un point stationnaire. Etudions l'allure de la courbe au voisinage de ce point.

Les signes de \(x(t)\) et \(y(t)\) renseignent sur le quadrant:

Puis, les signes de \(\dot{x}(t)\) et \(\dot{y}(t)\) renseignent sur la direction dans laquelle pointe \(\dot{\vec{r}}(t)\):
De plus, à l'approche du point stationnaire, la pente de \(\dot{\vec{r}}(t)\) tend vers \[ \lim_{t\to 0}\frac{\dot{y}(t)}{\dot{x}(t)}= \lim_{t\to 0}\frac{3t^2}{2t}= \lim_{t\to 0}\frac{3t}{2}=0\,. \] On en déduit que le point stationnaire \(M(0)=(0,0)\) est un ''point de rebroussement'', puisque la particule arrive depuis \(IV\), avec la pente du vecteur tangent proche de zéro, puis repart dans \(I\), avec la pente du vecteur tangent toujours proche de zéro.

Dernière compilation: 2024-06-03 (22:36:08)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)