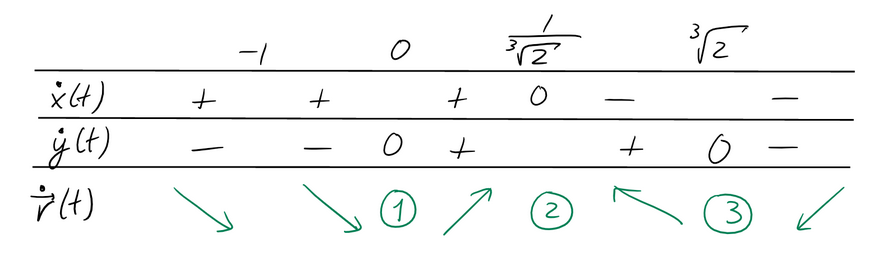Exemple: Sur \(D=\R \setminus\{1\}\), considérons la courbe paramétrée \(M(t)=(x(t),y(t))\), où \[ x(t)=\frac{1}{1-t}\,, \qquad y(t)=\frac{t^2}{1-t}\,. \] Etude des branches infinies: La courbe peut admettre des branches infinies aux bornes de son domaine: en \(\pm \infty\) et en \(1\).

• Lorsque \(t \to -\infty\), \[ \lim_{t\to -\infty} x(t)=0\,,\qquad \lim_{t\to -\infty} y(t)=+\infty\,. \] La courbe admet donc une asymptote verticale d'équation \(x = 0\). Remarquons que \(x(t) \gt 0\) pour \(t\lt 1\) et en particulier au voisinage de \(-\infty\); la courbe reste donc à droite de son asymptote lorsque \(t \to -\infty\).
• Lorsque \(t \to +\infty\), \[ \lim_{t\to -\infty} x(t)=0\,,\qquad \lim_{t\to -\infty} y(t)=-\infty\,. \] La courbe admet donc la même asymptote verticale d'équation \(x = 0\), avec \(x(t) \lt 0\) au voisinage de \(+\infty\); la courbe reste donc à gauche de son asymptote lorsque \(t \to +\infty\).
• Lorsque \(t\to -1^-\), \[ \lim_{t\to -1^-}x(t)= \lim_{t\to -1^-} y(t)=+\infty\,. \] Pour détecter une potentielle asymptote oblique lorsque \(t\) tend vers \(-1\) par la gauche, on calcule \[ \lim_{t\to -1^-} \frac{y(t)}{x(t)} =\lim_{t\to -1^-}t^2=1, \qquad \lim_{t\to -1^-} y(t)-1\cdot x(t) =\lim_{t\to -1^-}-(t+1)=-2\,. \] La courbe admet donc une asymptote oblique d'équation \(y=x-2\) lorsque \(t\to -1^-\).
  
  De plus, on peut vérifier que \(y(t)-(x(t)-2)=-t+1\) est positif pour \(t \lt 1\), en particulier pour \(t\) tendant vers \(1\) par la gauche; donc on sait que la courbe reste au-dessus de la droite \(y = x-2\) lorsque \(t \to -1^-\).
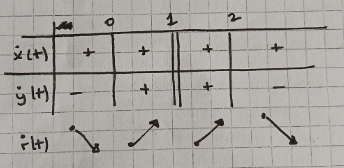
• Lorsque \(t \to -1^+\), un calcul similaire nous permet d'obtenir la même asymptote oblique d'équation \(y = x-2\) et de vérifier que la courbe reste au-dessous de cette asymptote. Etudions ensuite le vecteur tangent. On a \[ \dot{\vec{r}}(t)= \begin{pmatrix} \displaystyle\frac{1}{(1-t)^2}\\ \displaystyle\frac{2t-t^2}{(1-t)^2} \end{pmatrix}\,. \] \(\dot{x}(t) \gt 0\) pour tout \(t \in D\), et \[ \dot{y}(t)=0 \quad\Longleftrightarrow\quad 2t-t^2=0 \quad\Longleftrightarrow\quad t=0\text{ ou }t=2\,. \] La courbe admet donc deux points à tangente horizontale: \(M(0) = (1, 0)\) et \(M(2) = (-1, -4).\) De plus:
  

En mettant ensemble toutes ces informations, on peut esquisser le tracé de la courbe dans le plan :

Exemple: Sur \(D=\mathbb{R}\setminus \{\pm 1\}\), considérons la courbe \(M(t)=(x(t),y(t))\), où \[ x(t)=\frac{1}{t^2-1}\,,\qquad y(t)=\frac{t^2}{t-1}\,. \] Il y a a priori six régions de \(D\) dans lesquelles au moins une des fonctions prend des valeurs grandes: proche de \(\pm\infty\) et proche de \(t=\pm 1\) (à gauche ou à droite dans chaque cas). On va donc séparer l'analyse en considérant les six limites suivantes:

1. Lorsque \(t\to -\infty\), \[ \lim_{t\to -\infty} x(t)=0\,,\qquad \lim_{t\to -\infty} y(t)=-\infty\,, \] et donc la droite \(x=0\) est une asymptote verticale. (Se souvenir pour plus tard: pour des temps \(t\) très éloignés dans le passé, \(x(t)\) est proche de zéro, \(y(t)\) est grand, négatif.)
2. Lorsque \(t\to -1^-\), \[ \lim_{t\to -1^-} x(t)=+\infty\,,\qquad \lim_{t\to -1^-} y(t)=-\frac{1}{2}\,, \] et donc la droite \(y=-\frac{1}{2}\) est asymptote horizontale. (Se souvenir pour plus tard: pour des temps \(t\) peu avant \(t=-1\), \(x(t)\) est très grand, positif, et \(y(t)\) est proche de \(-\frac12\).)
3. Lorsque \(t\to -1^+\), \[ \lim_{t\to -1^+} x(t)=-\infty\,,\qquad \lim_{t\to -1^+} y(t)=-\frac{1}{2}\,, \] et donc la droite \(y=-\frac{1}{2}\) est asymptote horizontale. (Se souvenir pour plus tard: pour des temps \(t\) peu après \(t=-1\), \(x(t)\) est très grand, négatif, et \(y(t)\) est proche de \(-\frac12\).)
4. Lorsque \(t\to 1^-\), \[ \lim_{t\to 1^-} x(t)=-\infty\,,\qquad \lim_{t\to 1^-} y(t)=-\infty\,. \] On peut donc tester l'existence d'une asymptote oblique. Commençons par \[\begin{aligned} m =\lim_{t\to 1^-}\frac{y(t)}{x(t)} &=\lim_{t\to 1^-}\frac{t^2(t^2-1)}{t-1}\\ &=\lim_{t\to 1^-}\frac{t^2(t-1)(t+1)}{t-1} =2\,. \end{aligned}\] Ensuite, \[\begin{aligned} h =\lim_{t\to 1^-}(y(t)-2x(t)) &=\lim_{t\to 1^-}\left(\frac{t^2}{t-1}-2\frac{1}{t^2-1}\right)\\ &=\lim_{t\to 1^-}\frac{t^3+t^2-2}{t^2-1} =\frac{5}{2}\,. \end{aligned}\] Ainsi, la droite d'équation \(y=2x+\frac{5}{2}\) est asymptote oblique. (Se souvenir pour plus tard: pour des temps \(t\) peu avant \(t=1\), \(x(t)\) et \(y(t)\) sont tous deux grands, négatifs, et \(M(t)\) est proche de cette asymptote.)
5. Lorsque \(t\to 1^+\), \[ \lim_{t\to 1^+} x(t)=\infty\,,\qquad \lim_{t\to 1^+} y(t)=\infty\,. \] Les mêmes calculs que ceux du point précédent montrent que la même droite \(y=2x+\frac{5}{2}\) est asymptote oblique. (Se souvenir pour plus tard: pour des temps \(t\) peu après \(t=1\), \(x(t)\) et \(y(t)\) sont tous deux grands, positifs, et \(M(t)\) est proche de cette asymptote.)
6. Lorsque \(t\to+\infty\), \[ \lim_{t\to +\infty} x(t)=0\,,\qquad \lim_{t\to +\infty} y(t)=+\infty\,, \] et donc \(x=0\) est asymptote verticale. (Se souvenir pour plus tard: pour des temps \(t\) très éloignés dans le futur, \(x(t)\) est proche de zéro, \(y(t)\) est grand, positif.)

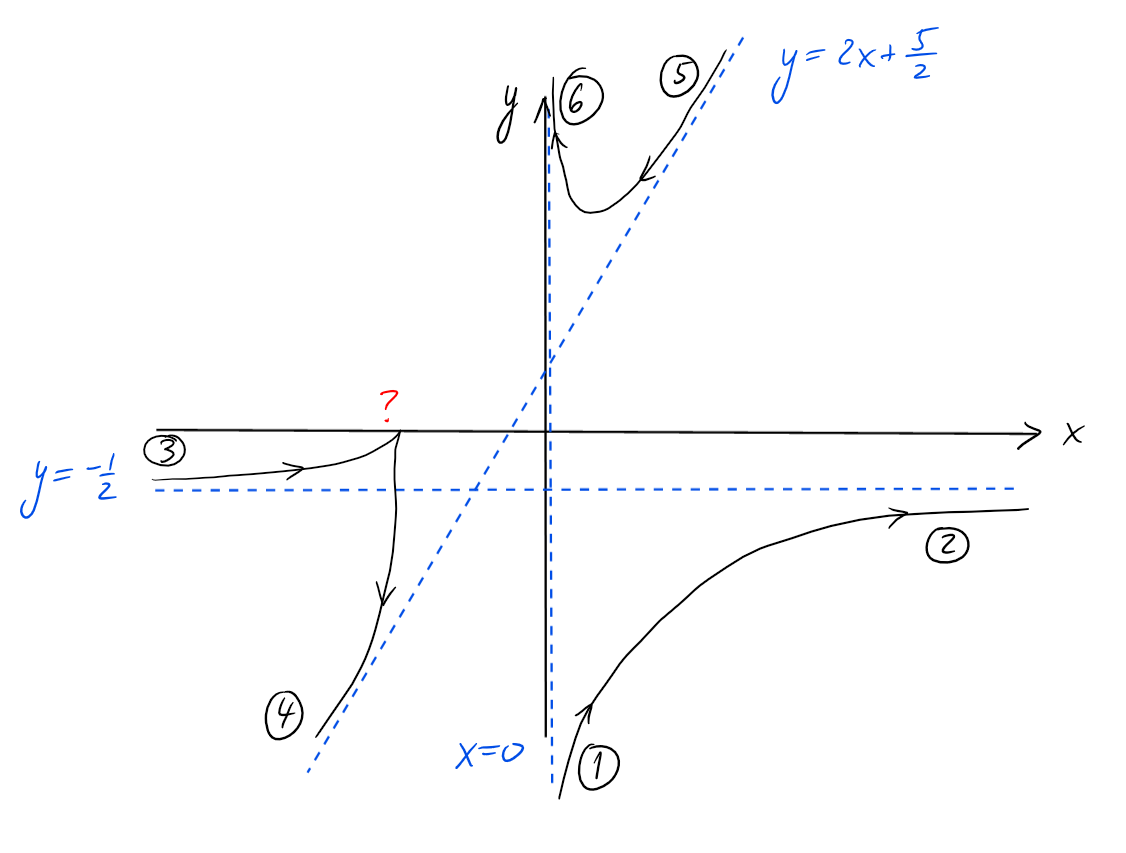
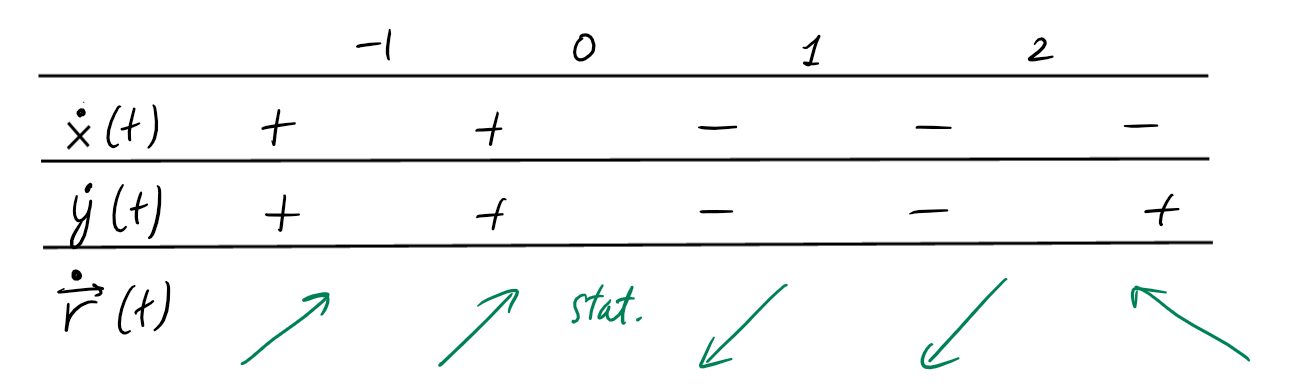
L'étude des branches infinies permet déjà de faire une première esquisse: Rendons l'analyse plus précise en étudiant le vecteur tangent. \[ \vec{r}(t)= \begin{pmatrix} \frac{1}{t^2-1}\\ \frac{t^2}{t-1} \end{pmatrix}\,,\qquad \dot{\vec{r}}(t)= \begin{pmatrix} \frac{-2t}{(t^2-1)^2}\\ \frac{t(t-2)}{(t-1)^2} \end{pmatrix}\,. \] On a donc

• un point de tangence horizontale en \(t=2\), \(M(2)=(\frac{1}{3},4)\),
• un point stationnaire en \(t=0\), \(M(0)=(-1,0)\)

L'étude des signes révèle le comportement du vecteur tangent sur le reste du domaine: Regardons ce qui se passe au voisinage du point stationnaire: \[ \lim_{t\to 0} \frac{\dot{y}(t)}{\dot{x}(t)} = \lim_{t\to 0} \frac{t(t-2)(t^2-1)^2}{(t-1)^2(-2t)} =1\,. \] Le point stationnaire est donc un ''point de rebroussement'', proche duquel la courbe a une pente proche de \(1\), indiquée en traitillé sur l'animation ci-dessous.

Exemple: Considérons la courbe de Lissajous définie par \[ \vec{r}(t) =\begin{pmatrix} \sin(t)\\ \sin(2t) \end{pmatrix}\,,\qquad t\in [-\pi,\pi]\,. \] Avant de commencer, deux remarques:

• \(x(t)\) et \(y(t)\) sont des fonctions impaires, donc la partie de la courbe pour \(t\in [-\pi,0]\) s'obtient à partir de la partie de la courbe pour \(t\in [0,\pi]\), par une rotation de \(180^{\circ}\) autour de l'origine.
• De plus, on peut remarquer que pour tout \(s\in \mathbb{R}\), \[ x(\tfrac{\pi}{2}-s)=x(s+\tfrac{\pi}{2})\,,\qquad y(\tfrac{\pi}{2}-s)=-y(\tfrac{\pi}{2}+s)\,, \] et donc la partie de la courbe avec \(t\in [\frac{\pi}{2},\pi]\) s'obtient à partir de la partie avec \(t\in [0,\frac{\pi}{2}]\), par une réflexion à travers \(Ox\).

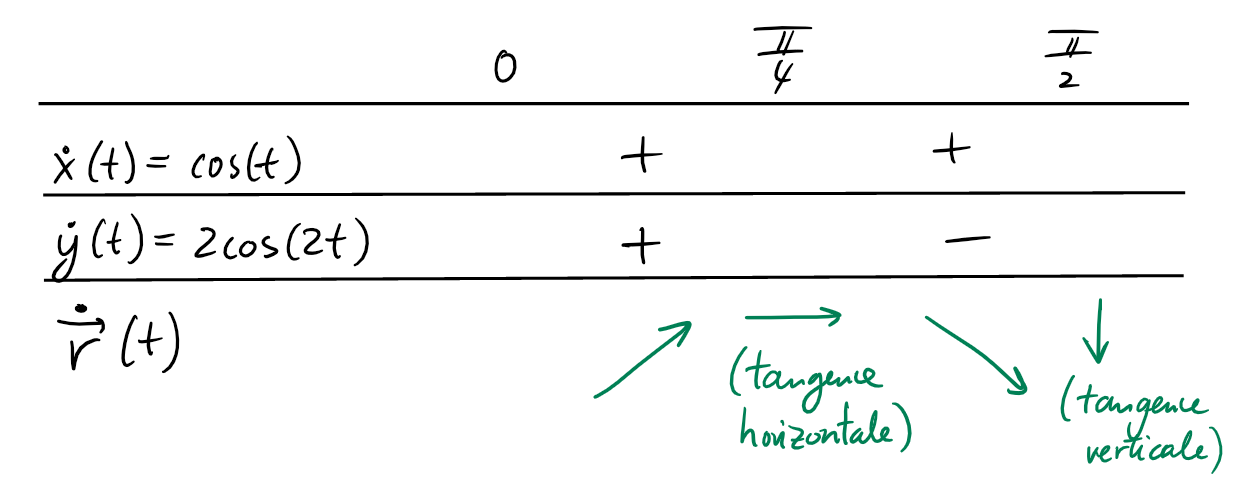
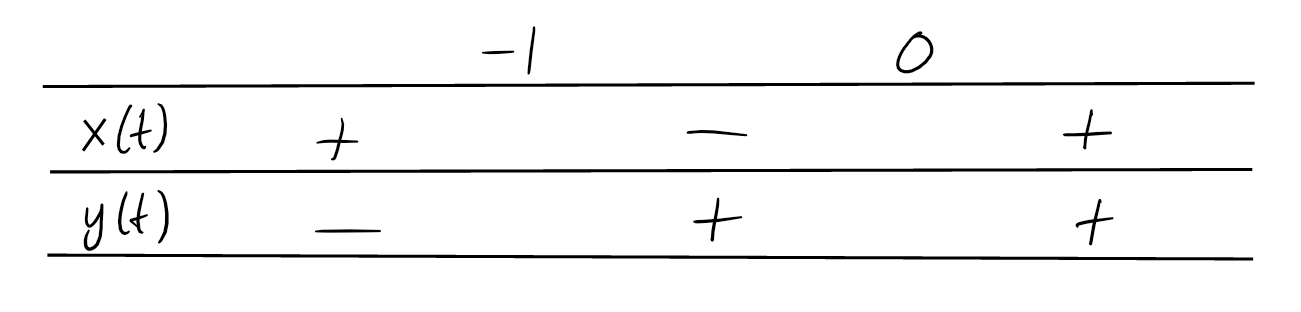
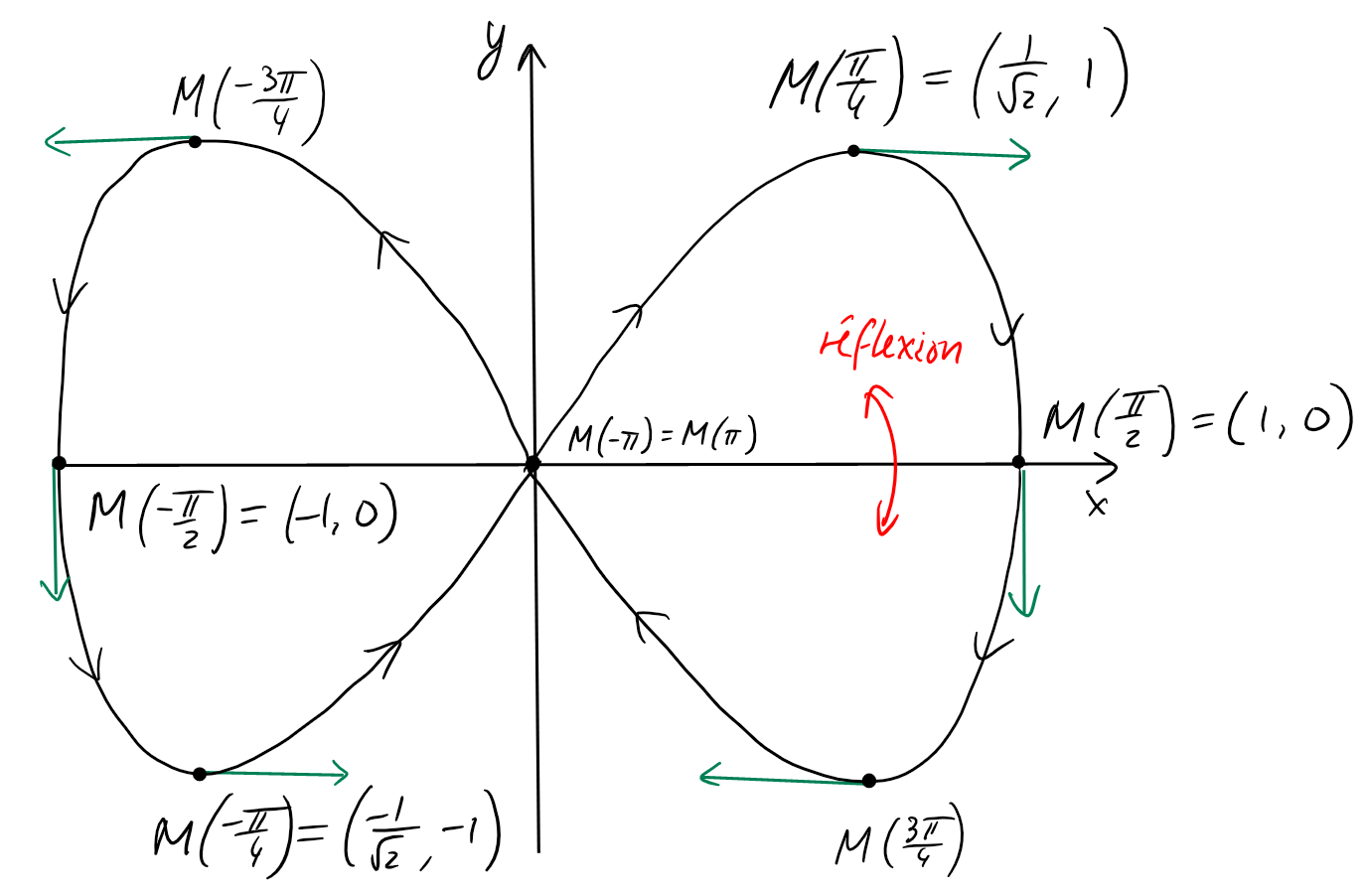
On peut donc se concentrer sur \(t\in [0,\frac{\pi}{2}]\). Sur cet intervalle, on a \(x(t)\geqslant 0\), \(y(t)\geqslant 0\), et les signes des dérivées \(\dot{x}(t)=\cos(t)\), \(\dot{y}(2)=2\cos(2t)\) sont donnés par: Remarquons aussi que \(M(0)=(0,0)\), \(M(\frac{\pi}{4})=(\frac{1}{\sqrt{2}},1)\), \(M(\frac{\pi}{2})=(1,0)\), et \[ \dot{\vec{r}}(t) =\begin{pmatrix} 1\\2 \end{pmatrix}\,. \] Ces informations permettent d'esquisser le tracé pour \(t\in [0,\frac{\pi}{2}]\), de le réfléchir à travers \(Ox\), puis d'effectuer une rotation du tout, de \(180^{\circ}\) autour de l'origine:

Exemple: Le Folium de Descartes est défini comme \[ \Gamma=\{(x,y)\in \mathbb{R}^2: x^3-3xy+y^3=0\}\,. \] Remarquons que si \((x,y)\in \Gamma\), alors \((y,x)\in \Gamma\).

Cherchons des points \((x,y)\in \Gamma\), de la forme \(y=tx\). En injectant dans la condition qui définit \(\Gamma\), on obtient \(x^3-3x(tx)+(tx)^3=0\), c'est-à-dire \[ x^2(x-3t+t^3x)=0\,. \] On a donc deux possibilités:

• \(x=0\), qui entraîne \(y=t0=0\), ou
• \(x=\frac{3t}{1+t^3}\), qui entraîne \(y=tx=\frac{3t^2}{1+t^3}\).

On peut donc étudier \(\Gamma\) à l'aide de la paramétrisation \[ x(t)=\frac{3t}{1+t^3}\,,\qquad y(t)=\frac{3t^2}{1+t^3}\,,\qquad t\in \mathbb{R}\setminus \{-1\}\,. \] Les dérivées sont \[ \dot{x}(t)=3\frac{1-2t^3}{(1+t^3)^2}\,, \qquad \dot{y}(t)=3\frac{t(2-t^3)}{(1+t^3)^2}\,, \] et l'étude des signes: On a donc

1. un point de tangence horizontale en \(M(0)=(0,0)\),
2. un point de tangence verticale en \(M(\frac{1}{\sqrt[3]{2}})=(2^{2/3},\sqrt{2})\),
3. un point de tangence horizontale en \(M(\sqrt[3]{2})=(\sqrt{2},2^{2/3})\) (le symétrique de \(M(\frac{1}{\sqrt[3]{2}})\) à travers la diagonale),
4. aucun point stationnaire.

Etudions les branches infinies.

Lorsque \(t\to -1\), \[ \lim_{t\to -1^{\mp}} x(t)=\pm \infty, \qquad \lim_{t\to -1^{\mp}} y(t)=\mp \infty \] On peut alors regarder \[\begin{aligned} m &=\lim_{t\to -1^{\mp}}\frac{y(t)}{x(t)} =\lim_{t\to -1^{\mp}}\frac{3t^2}{1+t^3}\cdot \frac{1+t^3}{3t}=-1\,, \end{aligned}\] puis \[\begin{aligned} h &= \lim_{t\to -1^{\mp}} [y(t)-(-1)x(t)]\\ &=\lim_{t\to -1^{\mp}}\left(\frac{3t^2}{1+t^3}+\frac{3t}{1+t^3}\right)\\ &=\lim_{t\to -1^{\mp}} \frac{3t(t+1)}{1+t^3}\\ &=\lim_{t\to -1^{\mp}}\frac{3t(t+1)}{(t+1)(t^2-t+1)}\\ &=\frac{-3}{3}=-1. 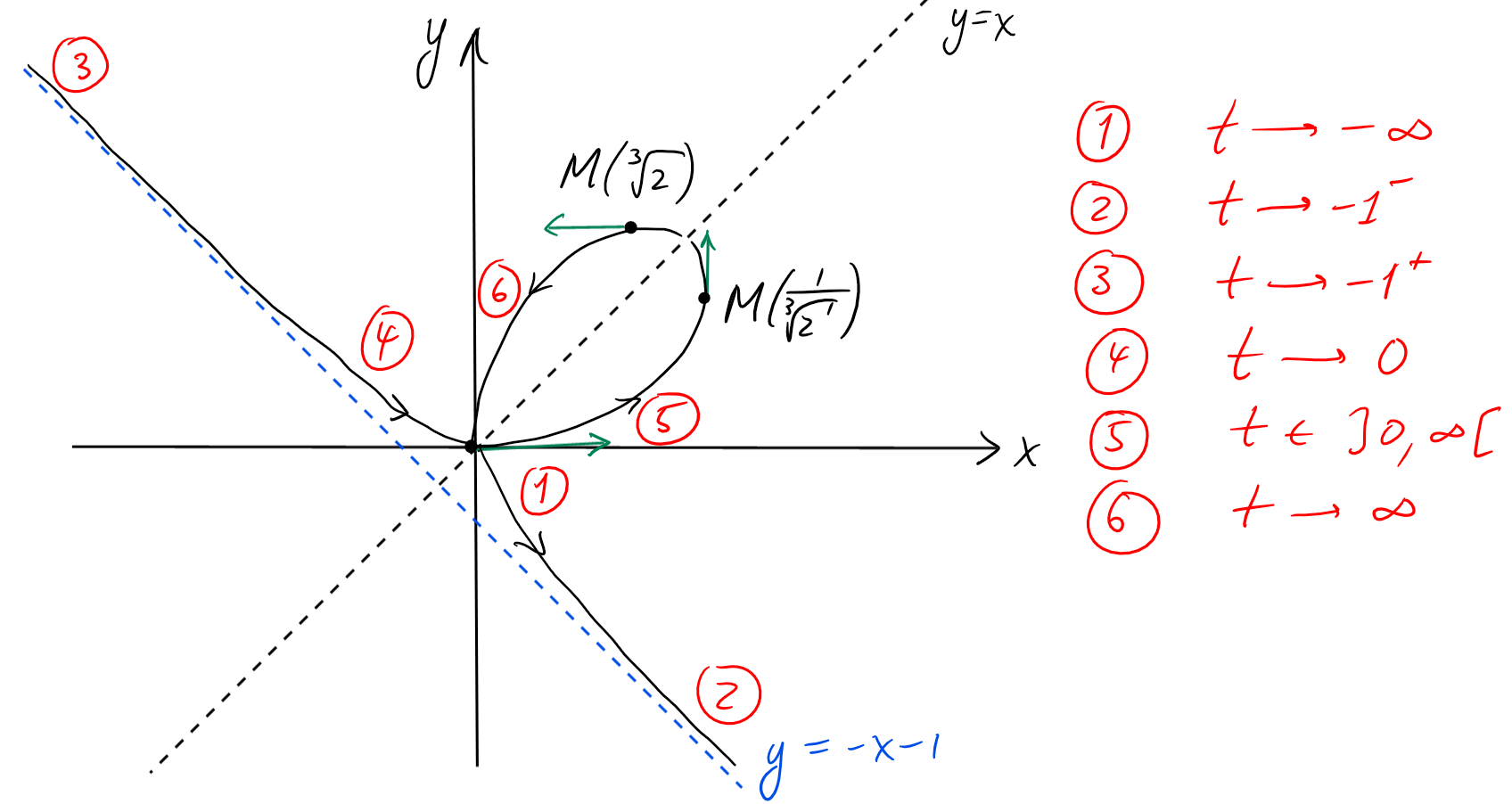\end{aligned}\] et donc \(y=-x-1\) est une asymptote oblique lorsque \(t \to -1^{\mp}\).

On remarque que \(\lim_{t\to \pm \infty} x(t)=\lim_{t\to \pm \infty} y(t)=0\).

Tracé: (On a aussi représenté la droite \(y=tx\).)

Exemple: Soient

• \(\gamma\) le cercle de rayon \(1\) centré à l'origine,
• \(A\) \(=(2,0)\),
• \(T\) \(\in \gamma\) (un point qui va bouger)
• \({\color{green}d}\) la tangente à \(\gamma\) en \(T\),
• \({\color{magenta}p}\) la droite perpendiculaire à \({\color{green}d}\) passant par \(A\),
• \(M\) le point d'intersection de \({\color{magenta}p}\) avec \({\color{green}d}\).

La trajectoire de \(M\), lorsque \(T\) se déplace sur \(\gamma\), est appelée le Limaçon de Pascal: Introduisons le paramètre \(t\in [-\pi,\pi]\) pour localiser \(T\) sur le cercle: \[ \overrightarrow{OT(t)}= \begin{pmatrix} \displaystyle \cos(t)\\ \displaystyle \sin(t) \end{pmatrix}\,. \] Puisque la tangente \({\color{green}d}\) est perpendiculaire à \(\overrightarrow{OT(t)}\), elle est dirigée par le vecteur \[ \begin{pmatrix} \displaystyle -\sin(t)\\ \displaystyle \cos(t) \end{pmatrix}\,. \] Pour une valeur fixée de \(t\), les expressions paramétriques de \({\color{green}d}\) et \({\color{magenta}p}\) sont \[\begin{aligned} {\color{green}d} &: \begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} \cos(t)\\ \sin(t) \end{pmatrix}+\lambda \begin{pmatrix} -\sin(t)\\ \cos(t) \end{pmatrix}, \quad \lambda \in \mathbb{R},\\ {\color{magenta}p} &: \begin{pmatrix} x\\ y \end{pmatrix}= \begin{pmatrix} 2\\ 0 \end{pmatrix}+\mu \begin{pmatrix} \cos(t)\\ \sin(t) \end{pmatrix}, \quad \mu \in \mathbb{R}. \end{aligned}\] Puisque \(M(t)\) est le point d'intersection de ces deux droites, on pose \[\begin{pmatrix} \cos(t)\\ \sin(t) \end{pmatrix}+\lambda \begin{pmatrix} -\sin(t)\\ \cos(t) \end{pmatrix}= \begin{pmatrix} 2\\ 0 \end{pmatrix}+\mu \begin{pmatrix} \cos(t)\\ \sin(t) \end{pmatrix}\,, \] que l'on résout pour trouver \[\begin{aligned} \lambda &=-2\sin(t)\\ \mu &= 1-2\cos(t). 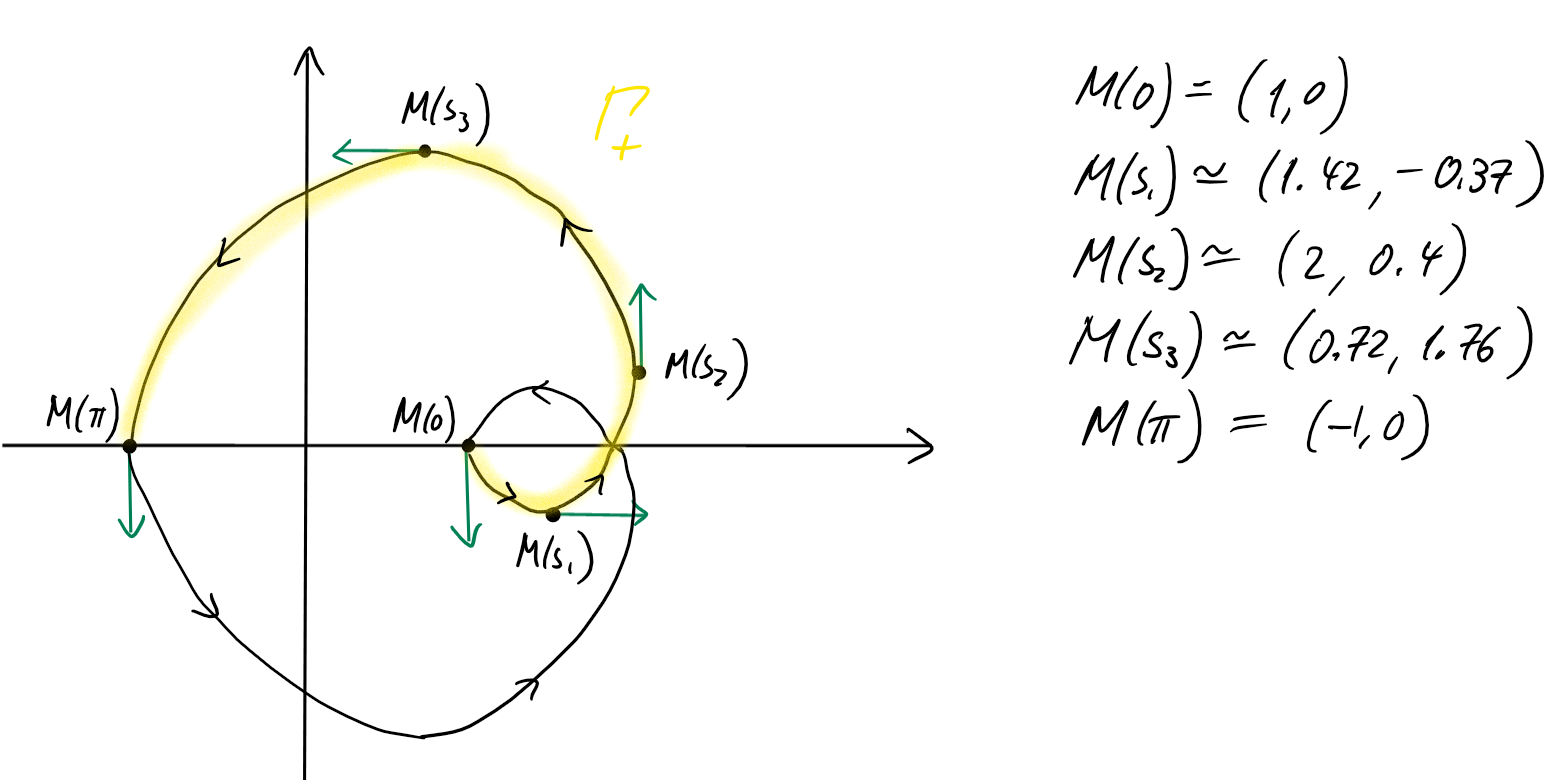\end{aligned}\] On a donc le point d'intersection \(M(t)=(x(t),y(t))\), où \[\begin{aligned} x(t)&=\cos(t)+2\sin^2(t),\\ y(t)&=\bigl(1-2\cos(t)\bigr)\sin(t). \end{aligned}\] On étudie le Limaçon ainsi paramétré, pour \(t\in[-\pi,\pi]\).

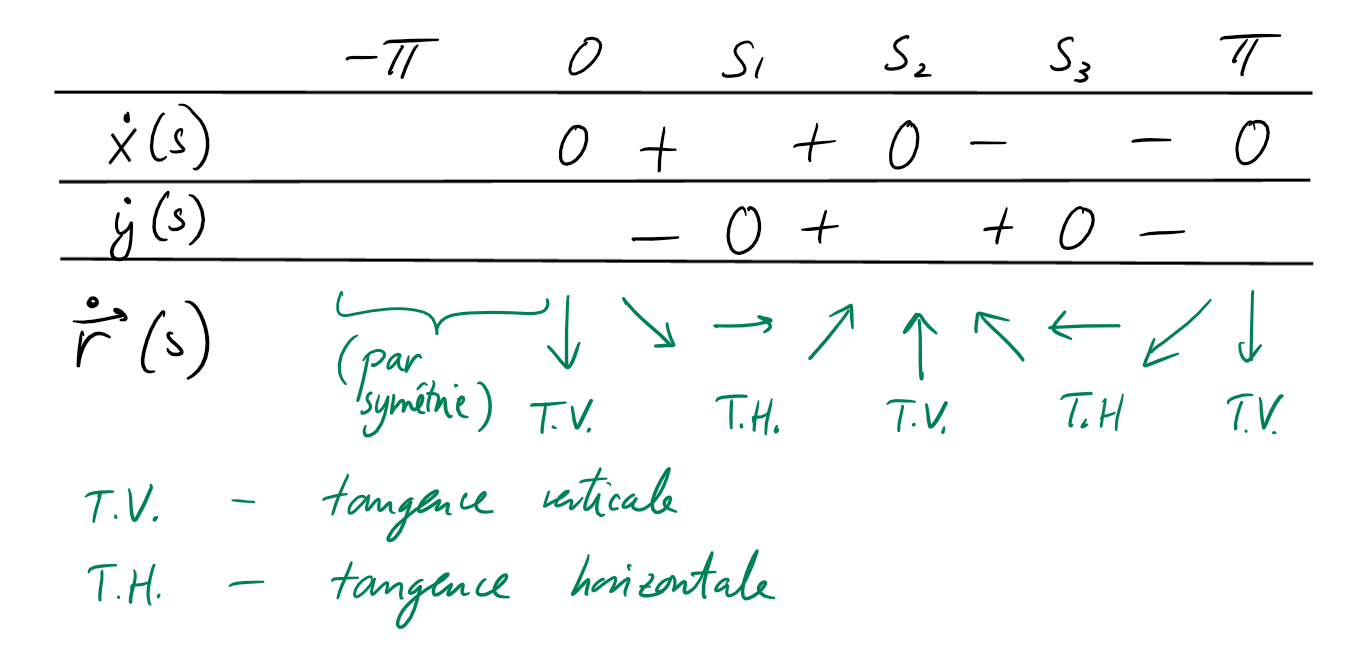
Les dérivées sont \[\begin{aligned} \dot{x}(t)&=-\sin(t)\bigl(1-4\cos(t)\bigr),\\ \dot{y}(t)&=-4\cos^2(t)+\cos(t)+2, \end{aligned}\] et on a

• \(\dot{x}(t)=0\) si et seulement si \(\sin(t)=0\) ou \(\cos(t)=\frac{1}{4}\), ce qui implique \(t=0\), \(t=\pm \pi\), ou \(t=\pm s_2\), où \[ s_2:= \arccos\left(\frac{1}{4}\right)\approx 75.6^{\circ} \]
• \(\dot{y}(t)=0\) si et seulement si \(\cos(t)=\frac{1\pm\sqrt{33}}{8}\) ce qui implique \(t=s_1\) ou \(s_3\), où \[\begin{aligned} s_1&:=\arccos\left(\frac{1-\sqrt{33}}{8}\right)\approx 32^{\circ} \,,\\ s_3&:=\arccos\left(\frac{1+\sqrt{33}}{8}\right)\approx 126.3^{\circ} \end{aligned}\]

On remarque que \(x(t)\) est paire et \(y(t)\) est impaire, donc la partie \(t\in[-\pi,0]\) s'obtient à partir de la partie \(t\in[0,\pi]\) par réflexion à travers \(Ox\).