6.3 Branches infinies

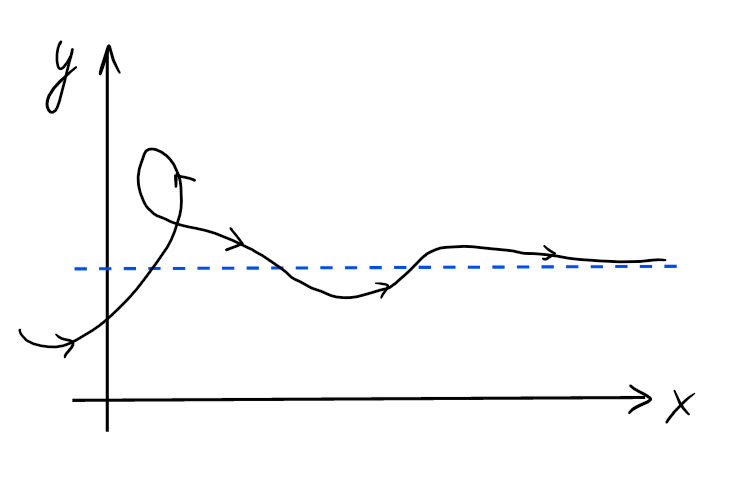
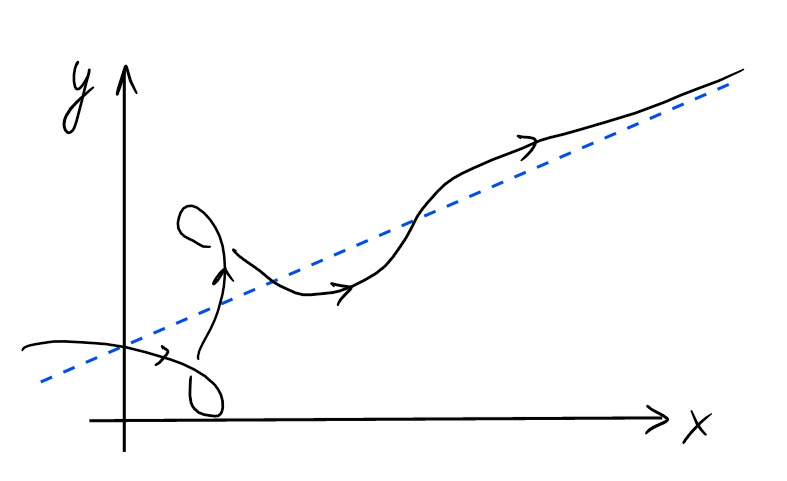
Comme pour les fonctions, l'étude d'une courbe pourra inclure l'analyse des branches infinies, à savoir les parties de la courbe (s'il y en a) qui contiennent des points situés arbitrairement loin de l'origine.

Une cours paramétrée \[\begin{aligned} M : D &\longrightarrow \mathbb{R}^2\\ t &\longmapsto M(t)=\left( x(t),y(t) \right). \end{aligned}\] possède une branche infinie s'il existe une région du domaine \(D\) dans laquelle au moins une des fonctions, (\(x(t)\) ou \(y(t)\)) prend des valeurs arbitrairement grandes. Cette région sera soit au voisinage d'un point, soit lorsque \(t\to\pm \infty\) lorsque c'est possible.

• Si \(x(t)\to \pm \infty\) et \(y(t)\to L\), alors la droite horizontale \(y=L\) est une asymptote horizontale.
  
• Si \(x(t)\to L\) et \(y(t)\to \pm \infty\), alors la droite verticale d'équation \(x=L\) est une asymptote verticale.
  
• Si \(x(t)\to \pm \infty\) et \(y(t)\to \pm \infty\), et si \[\begin{aligned} m &:=\lim \frac{y(t)}{x(t)}\in \mathbb{R}\,, \quad \text{ et}\\ h &:=\lim (y(t)-m\cdot x(t))\in\mathbb{R}, \end{aligned}\] alors la droite d'équation \(y=mx+h\) est une asymptote oblique.
  
  Si \(\lim [y(t)-m\cdot x(t)]=\pm \infty\), il s'agit d'une branche parabolique de pente \(m\).

---

Dernière compilation: 2024-06-03 (22:36:08)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)