4.1 Introduction
On a vu que la valeur qu'une fonction \(f\) prend un un point
\(x_0\) peut n'avoir aucun lien avec la valeur de sa limite
\(\lim_{x\rightarrow x_0} f(x)\).
Pour certaines fonctions, pourtant, la
limite \(\lim_{x\rightarrow x_0} f(x)\) est égale
à la valeur \(f(x_0)\) de
\(f\) en \(x_0\). Ces fonctions sont dites continues.
Si \(f\) est définie en \(x_0\in\mathbb{R}\) et dans son voisinage, et si
\[
\lim_{x\rightarrow x_0} f(x)=f(x_0)\,,
\]
on dit que \(f\) est continue en \(x_0\).
Sinon, \(f\) est dite discontinue en \(x_0\).
La définition de continuité comporte implicitement trois exigences:
- \(f(x_0)\) existe, c'est-à-dire \(x_0\in D_f\),
- \(\lim_{x\rightarrow x_0} f(x)\) existe,
\(\lim_{x\rightarrow x_0} f(x)=L\in\mathbb{R}\), et
- cette limite \(L=f(x_0)\).
Exemple:
La fonction \(f(x)=x^2\) est continue en \(2\), puisque
\(\lim_{x\rightarrow 2}f(x)=4\) (voir section précédente), et
\(f(2)=2^2=4\), donc \(\lim_{x\rightarrow 2} f(x)=f(2)\).
On remarque qu'il est donc très facile de calculer les limites des fonctions
continues: pour trouver \(\lim_{x\rightarrow x_0} f(x)\), on doit simplement
évaluer la fonction \(f\) en \(x_0\).
Considérons quelques exemples de fonctions discontinues:
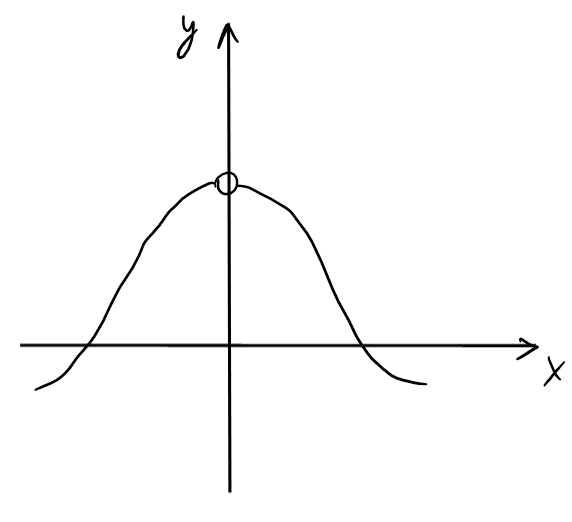
- Discontinuité de type ''trou'':
\(\lim_{x\rightarrow x_0} f(x)\) existe
mais \(f\) n'est pas définie en \(x_0\).
Par exemple, \(f(x)=\frac{\sin(x)}{x}\) en \(x_0=0\).
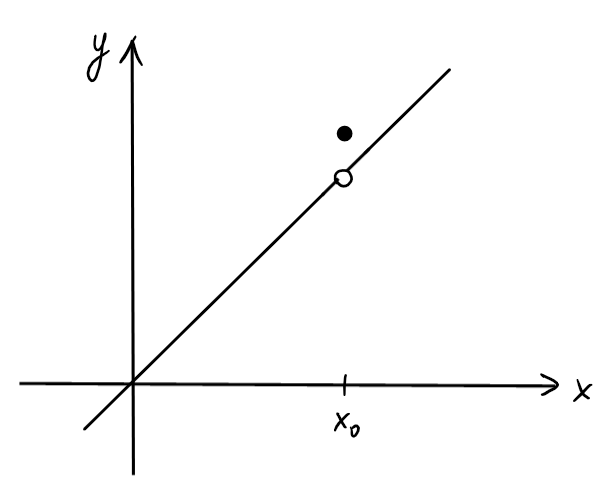
- Discontinuité de type ''trou-saut'': \(f(x_0)\) existe,
\(\lim_{x\rightarrow x_0} f(x)\) existe aussi, mais
\(f(x_0)\neq \lim_{x\rightarrow x_0} f(x)\).
Par exemple, si
\[
f(x)=
\begin{cases}
x & \text{ si } x\neq 5,\\
6 & \text{ si } x=5\,,
\end{cases}
\]
alors avec \(x_0=5\) on a \(f(x_0)=6\) mais \(\lim_{x\to x_0}f(x)=5\):
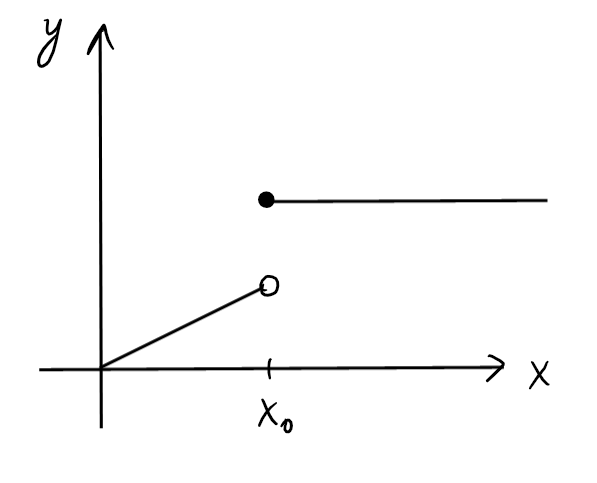
- Discontinuité de type ''saut'':
\(\lim_{x\rightarrow x_0^+} f(x)\) et
\(\lim_{x\rightarrow x_0^-} f(x)\) existent
mais ne sont pas égales
(et donc \(\lim_{x\rightarrow x_0} f(x)\) n'existe pas). Par exemple,
\[
f(x)=
\begin{cases}
\frac{x}{2} & \text{ si } x\lt 2,\\
2 & \text{ si } x\geqslant 2
\end{cases}
\]
en \(x_0=2\):
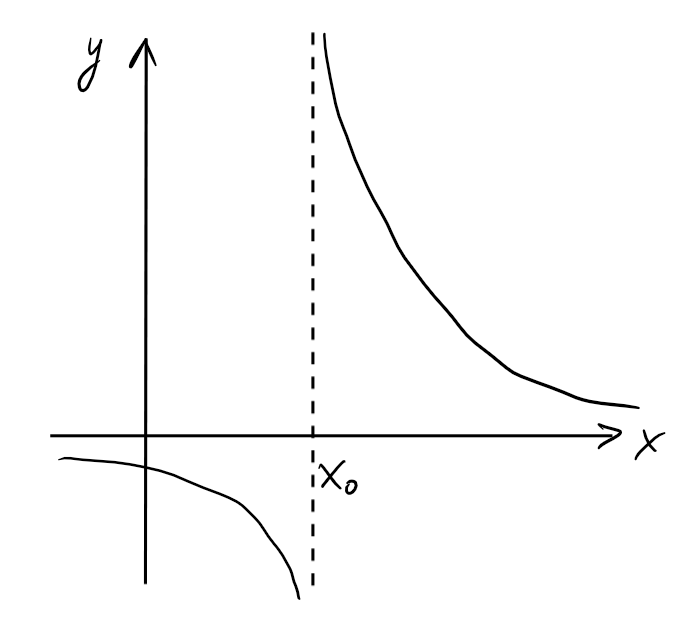
- Discontinuité de type infini:
Au moins une des limites
\(\lim_{x\rightarrow x_0^-} f(x)\),
\(\lim_{x\rightarrow x_0^+} f(x)\)
ou \(\lim_{x\rightarrow x_0} f(x)\)
est \(\pm \infty\).
Par exemple, \(f(x)=\frac{1}{x-2}\) est discontinue en \(x_0=2\).
On peut expliciter la définition de la continuité en remplaçant la limite par sa
définition:
\(f\) est continue en \(x_0\) si
\(\forall \varepsilon\gt 0\), \(\exists \delta\gt 0\) tel que
\[
|x-x_0|\leqslant \delta
\quad\Longrightarrow\quad
|f(x)-f(x_0)|\leqslant \varepsilon\,.
\]
Remarquons que pour la continuité, on s'intéresse justement à ce qui se passe en
\(x_0\), et on remplace donc la condition ''\(0\lt |x-x_0|\leqslant \delta\)'', dans la
définition de limite, par ''\(|x-x_0|\leqslant \delta\)''.
Soit \(I\) un intervalle ouvert. Une fonction \(f\) est dite continue sur \(I\) si elle est continue en \(x_0\) pour tout \(x_0\in I\).
L'ensemble de toutes les fonctions continues sur \(I\) est
noté \(C^0(I)\).
Intuitivement,
une fonction est continue sur \(I\) si on peut y tracer son graphe ''sans lever
le crayon''.
Exemple:
Montrons que \(f(x)=x^2\) est continue en tout \(x_0\). Soit
\(\varepsilon\gt 0\). On cherche \(\delta\gt 0\) tel que \(|x-x_0|\leqslant \delta
\Longrightarrow |f(x)-f(x_0)|\leqslant \varepsilon\).
On a
\[\begin{aligned}
|f(x)-f(x_0)|&=|x^2-x_0^2|\\
&=|(x-x_0)\cdot(x+x_0)|\\
&=|x-x_0|\cdot|x+x_0|\\
&=|x-x_0|\cdot|x-x_0+x_0+x_0|\\
&\leqslant|x-x_0|\cdot\left(|x-x_0|+|2x_0|\right)\\
&=|x-x_0|^2+|2x_0|\cdot |x-x_0|.
\end{aligned}\]
On doit donc choisir \(\delta\gt 0\) tel que
\[
|x-x_0|\leqslant\delta
\quad\Longrightarrow\quad
|x-x_0|^2+|2x_0|\cdot |x-x_0|
\leqslant \varepsilon\,.
\]
On a
\[
|x-x_0|\leqslant\delta
\quad\Longrightarrow\quad
|x-x_0|^2+|2x_0|\cdot |x-x_0|
\leqslant \delta^2+|2x_0|\cdot\delta\,.
\]
On peut donc prendre \(\delta\gt 0\) tel que \(\delta^2+|2x_0|\cdot\delta\leqslant \varepsilon\).
En exigeant que \(\delta\leqslant 1\), on a
\(\delta^2+|2x_0|\cdot\delta=\delta(\delta+|2x_0|)\leqslant \delta(1+2|x_0|)\), et
donc il suffit de prendre \(\delta\gt 0\) tel que
\(\delta(1+2|x_0|)\leqslant \varepsilon\),
c'est-à-dire
\(\delta\leqslant \frac{\varepsilon}{1+2|x_0|}\).
Ainsi, en prenant
\(0\lt \delta\leqslant \min\{1,\frac{\varepsilon}{1+2|x_0|}\}\),
on a
\[
|x-x_0|\leqslant\delta
\quad\Longrightarrow\quad
|f(x)-f(x_0)|\leqslant \varepsilon\,.
\]
Exemples:
- Soit \(f(x)=\sin(x)\), et soit \(x_0\in \mathbb{R}\) un point fixé.
Montrons que \(f\) est continue en \(x_0\).
Soit \(\varepsilon\gt 0\).
On cherche \(\delta\gt 0\) tel que \(|x-x_0|\leqslant \delta \Longrightarrow
|f(x)-f(x_0)|\leqslant \varepsilon\).
On remarque pour commencer que
\[\begin{aligned}
|f(x)-f(x_0)|&=|\sin(x)-\sin(x_0)|\\
&=\left|2\cos\left(\frac{x+x_0}{2}\right)\sin\left(\frac{x-x_0}{2}\right)\right|\\
&=2\left|\cos\left(\frac{x+x_0}{2}\right)\right|\cdot\left|\sin\left(\frac{x-x_0}{2}\right)\right|\\
&\leqslant 2\left|\sin\left(\frac{x-x_0}{2}\right)\right|\\
&\leqslant 2 \frac{|x-x_0|}{2}\\
&=|x-x_0|.
\end{aligned}\]
Prenons maintenant un \(\delta\) tel que
\(0\lt \delta\leqslant \varepsilon\). On a alors, pour ce \(\delta\), que
\[\begin{aligned}
|x-x_0|\leqslant \delta
\quad\Longrightarrow\quad
|f(x)-f(x_0)|
&\leqslant |x-x_0|\\
&\leqslant \delta\\
&\leqslant \varepsilon\,.
\end{aligned}\]
Ceci montre que \(f\)
est continue en \(x_0\). On a donc montré que \(f\in C^0(\mathbb{R})\).
- En utilisant l'identité
\[\cos(x) - \cos(x_0) = -2\sin\left(\frac{x+x_0}{2}\right)\sin\left(\frac{x-x_0}{2}\right),\]
on prouve de même que \(\cos(x)\) est continue en tout \(x_0\in\mathbb{R}\).
Soient \(f\) et \(g\) continues en \(x_0\). Alors les fonctions suivantes sont aussi continues en \(x_0\):
- \(\lambda f\) pour \(\lambda\in\mathbb{R}\),
- \(|f|\),
- \(f\pm g\),
- \(f\cdot g\),
- \(\frac{f}{g}\) (si \(g(x_0)\neq 0\)).
Ces propriétés sont conséquences des propriétés des limites. Par exemple,
\(f\) et \(g\) sont continues en \(x_0\) \(\iff\) \(\lim_{x\rightarrow x_0} f(x)=f(x_0)\) et \(\lim_{x\rightarrow x_0} g(x)=g(x_0)\). On a donc \(\lim_{x\rightarrow x_0} (f(x)+g(x))=f(x_0)+g(x_0)\), et donc \(\lim_{x\rightarrow x_0} (f+g)(x)=(f+g)(x_0)\), d'où \(f+g\) est continue en \(x_0\).
Exemples:
- En utilisant ces propriétés, la preuve de la continuité de \(f(x)=x^2\)
devient
immédiate: comme la fonction identité \(g(x) = x\) est continue (puisque pour
tout \(x_0\), on a
\(\lim_{x \to x_0} g(x) = \lim_{x \to x_0} x = x_0 = g(x_0)\)), on a que
\(f(x)=g(x)^2=g(x)g(x)\)
est continue en \(x_0\), étant donné que c'est un
produit de fonctions continues en \(x_0\).
- De même, comme
les fonctions constantes sont continues,
on en déduit que les polynômes sont des fonctions continues en tout
\(x_0\), puisque ce sont des sommes de produits de fonctions continues.
- Il en découle aussi que les fonctions rationnelles (de la forme
\(f(x) = \frac{P(x)}{Q(x)}\), où \(P\) et \(Q\) sont des polynômes)
sont continues sur leur domaine.
- \(\tan(x) = \frac{\sin(x)}{\cos(x)}\) est continue sur son domaine
puisqu'elle est donnée par le quotient de deux fonctions continues.
- \(\exp(x)\) et
\(\log(x)\) sont continues sur leurs domaines de définitions respectifs (on ne
le démontre pas).
Théorème:
Soit \(f\) définie sur un voisinage épointé de \(x_0\) telle que \(\lim_{x\rightarrow x_0} f(x)=L\in \mathbb{R}\), et soit \(g\) continue au point \(L\). Alors
\[\lim_{x\rightarrow x_0} g(f(x))=g(\lim_{x\rightarrow x_0} f(x))=g(L).\]
Le théorème ci-dessus dit qu'on peut ''passer les limites à l'intérieur d'une
fonction continue''.
Exemple:
Considérons la limite
\[
\lim_{x\to 0}\sqrt{1+\sin(x)}\,.
\]
On peut écrire \(\sqrt{1+\sin(x)}=g(f(x))\), où \(g(x)=\sqrt{x}\),
\(f(x)=1+\sin(x)\).
On sait que
\(\lim_{x\to 0}f(x)=1\), et puisque
\(g\) est continue en \(1\), on peut ''rentrer la limite dans \(g\)'':
\[
\lim_{x\to 0}\sqrt{1+\sin(x)}
=\sqrt{\lim_{x\to 0}(1+\sin(x))}
=\sqrt{1}=1\,.\]
Une conséquence du théorème:
Si \(f\) est continue en \(x_0\) et \(g\) est continue en \(f(x_0)\), alors la
composition \(g\circ f\) est continue en \(x_0\).
La caractérisation par les suites implique la caractérisation suivante de la
continuité.
Théorème:
\(f\) est continue en \(x_0\) \(\iff\) pour toute suite \((x_n)\) telle que \(x_n\rightarrow x_0\), on a \(\lim_{n\rightarrow \infty} f(x_n)=f(x_0)\).
On peut utiliser ce théorème pour montrer qu'une fonction n'est pas continue.
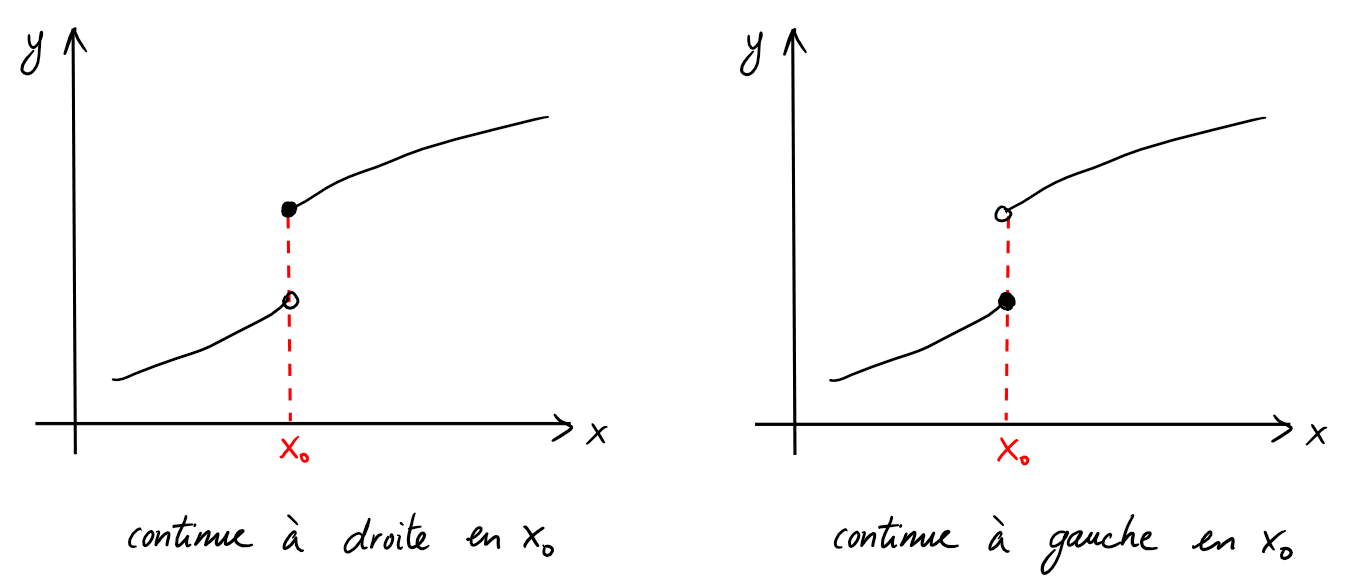
- Si \(\lim_{x\rightarrow x_0^+}f(x)=f(x_0)\), la fonction \(f\) est dite
continue à droite.
- Si \(\lim_{x\rightarrow x_0^-}f(x)=f(x_0)\), la fonction \(f\) est dite
continue à gauche.
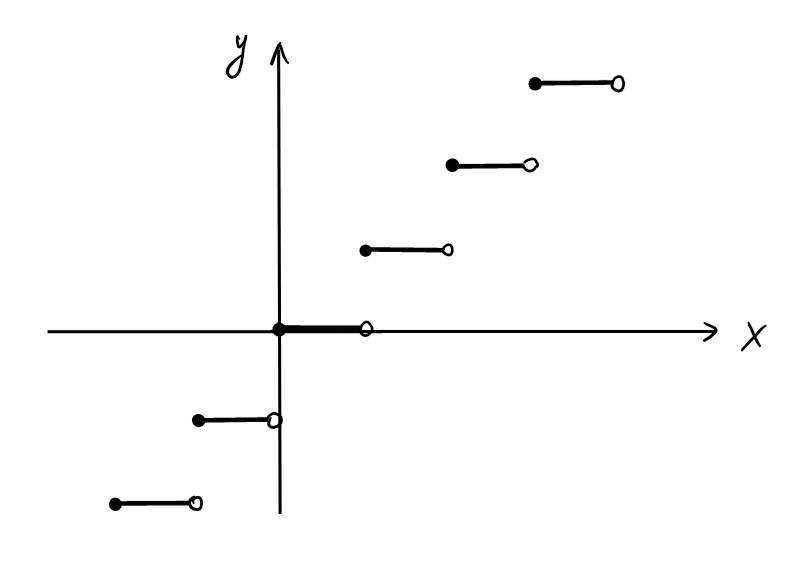
Exemples:
- \(f(x)=E(x)\) est continue à droite et discontinue à gauche en tout \(x_0\in \mathbb{Z}\).
En effet, si \(x_0\in\mathbb{Z}\),
\[
\lim_{x\rightarrow x_0^-}E(x)=E(x_0)-1=x_0-1\neq x_0=E(x_0)\,.
\]
- Soit \(f:[-2,+\infty[\to\mathbb{R}\) définie par
\[
f(x)=
\begin{cases}
\frac{\sqrt{2+x}-2}{x-2} & \text{ si } x\lt 2,\\
\frac{1}{4} & \text{ si } x= 2\\
2x^2-4 & \text{ si } x\gt 2.
\end{cases}
\]
Discutons de la continuité de \(f\) en \(x_0=2\). On a
\[\begin{aligned}
\lim_{x\rightarrow 2^-}f(x)&= \lim_{x\rightarrow 2^-}\frac{\sqrt{2+x}-2}{x-2}\\
&=\lim_{x\rightarrow 2^-}\frac{\left(\sqrt{2+x}-2\right)\left(\sqrt{2+x}+2\right)}{(x-2)\left(\sqrt{2+x}+2\right)}\\
&=\lim_{x\rightarrow 2^-} \frac{x-2}{(x-2)\left(\sqrt{2+x}+2\right)}\\
&=\lim_{x\rightarrow 2^-}\frac{1}{\sqrt{2+x}+2}=\frac{1}{4}, \text{ et}\\
\lim_{x\rightarrow 2^+}f(x)&= \lim_{x\rightarrow 2^+} 2x^2-4 =4.
\end{aligned}\]
On a \(\lim_{x\rightarrow 2^-}f(x)=\frac{1}{4}=f(2)\) et la fonction est donc continue à gauche en \(2\). Par contre, puisque \(\lim_{x\rightarrow 2^+}f(x)\neq f(2)\), la fonction n'est pas continue à droite.