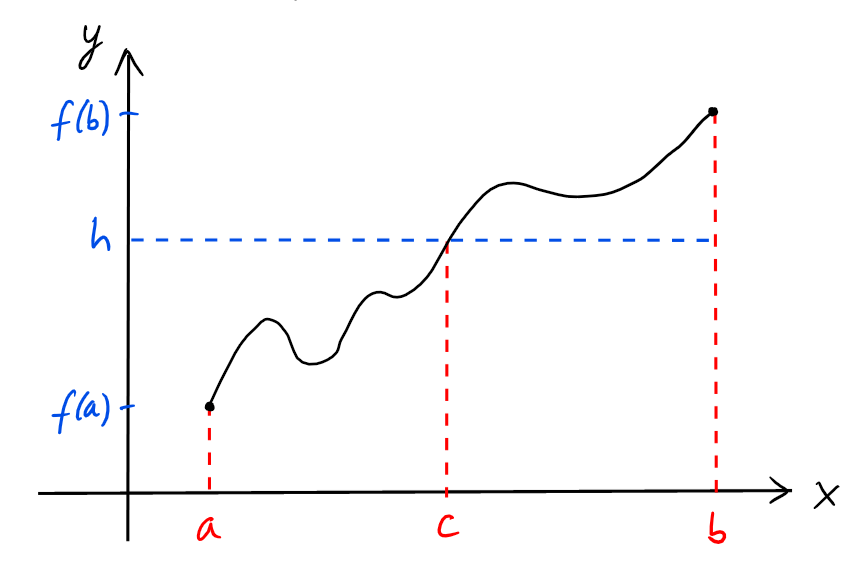
4.2 Théorème de la valeur intermédiaire
Une fonction \(f:[a,b]\rightarrow \mathbb{R}\) est dite continue si

Théorème:[Théorème de la valeur intermédiaire (TVI)] Soit \(f:[a,b]\rightarrow \mathbb{R}\) continue, telle que \(f(a)\lt f(b)\). Alors pour tout \(h\in \ ]f(a),f(b)[\), il existe \(c\in \ ]a,b[\) tel que \(f(c)=h\).

Soit \(f:[a,b]\rightarrow \mathbb{R}\) continue, telle que \(f(a)\lt f(b)\), et soit \(h\in \ ]f(a),f(b)[\). On va utiliser un algorithme de bissection pour construire \(c\in \ ]a,b[\) tel que \(f(c)=h\) comme une limite de suites. On procède par étapes:

Etape 1: Soit \(a_0 = a\) et \(b_0 = b\). On considère le milieu \(\frac{a_0+b_0}{2}\) de \([a_0, b_0]\).

  • Si \(f\left(\frac{a_0+b_0}{2}\right) = h\), on a trouvé \(c\in \ ]a,b[\) tel que \(f(c)=h\). Sinon,
  • si \(f\left(\frac{a_0+b_0}{2}\right) \lt h\), on pose \(a_1 = \frac{a_0+b_0}{2}\) et \(b_0 = b\)
  • si \(f\left(\frac{a_0+b_0}{2}\right) \gt h\), on pose \(a_1 = a_0\) et \(b_1 = \frac{a_0+b_0}{2}\).
Dans les deux derniers cas, on s'est ramené à un intervalle \([a_1, b_1]\) de longueur \(\frac{b-a}{2}\), avec \(f(a_1) \lt h\) et \(f(b_1) \gt h\).

Etape 2: On considère le milieu de l'intervalle \([a_1, b_1]\): soit on obtient un \(c\in \ ]a,b[\) tel que \(f(c)=h\), soit on se ramène à un intervalle \([a_2, b_2]\) de longueur \(\frac{b-a}{4}\), avec \(f(a_2) \lt h\) et \(f(b_2) \gt h\).

On répète cette procédure de telle sorte qu'à l'issue de l'étape \(n\), si on n'a pas encore trouvé un \(c\in \ ]a,b[\) tel que \(f(c)=h\), on a défini un intervalle \([a_n, b_n] \subset [a,b]\), de longueur \(\frac{b-a}{2^n}\), avec \(f(a_n) \lt h\) et \(f(b_n) \gt h\).

On obtient ainsi:
  • Une suite \((a_n)\) croissante et majorée par \(b\)
  • Une suite \(b_n\) décroissante et minorée par \(a\).
Ces deux suites convergent, et on a de plus que \[ \lim_{n \to \infty} (b_n - a_n) = \lim_{n \to \infty} \frac{b-a}{2^n} = 0\,, \] donc \(\lim_{n \to \infty} b_n = \lim_{n \to \infty} a_n \). On définit \[c = \lim_{n \to \infty} a_n = \lim_{n \to \infty} b_n.\] Il nous reste à prouver que \(f(c) = h\). Par la continuité de \(f\) et puisque \(a_n \to c\), le théorème de caractérisation de la continuité par les suites nous permet de dire que \(\lim_{n \to \infty} f(a_n) = f(c)\). De même, \(\lim_{n \to \infty} f(b_n)=f(c)\).

Or pour tout \(n\), \(f(a_n) \lt h\), donc \( \lim_{n \to \infty} f(a_n) \leqslant h\). De même, pour tout \(n\), \(f(b_n) \gt h\), donc \( \lim_{n \to \infty} f(a_n) \geqslant h\). Donc \(\lim_{n \to \infty} b_n = \lim_{n \to \infty} a_n \) implique que \[\lim_{n \to \infty} a_n = \lim_{n \to \infty} b_n = h\] et enfin que \(f(c) = h\).

On remarque que sans l'hypothèse de continuité, le résultat n'est plus vrai en général.

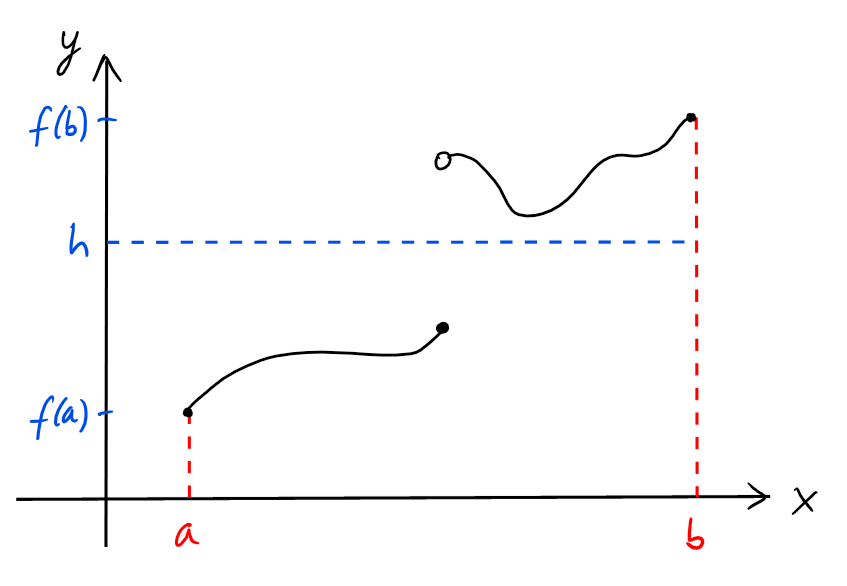
Exemple: On peut utiliser le TVI pour fournir une solution approximative d'une équation (et, en particulier, montrer qu'une solution existe). Considérons l'équation \(x^5=1-x\). On pose \(f(x)=x^5+x-1\), une fonction continue. Sur l'intervalle \([0,1]\), on a \[\begin{aligned} f(0)&=-1,\\ f(1)&=1. \end{aligned}\] On prend \(h:=0\). Par le TVI, il existe \(c\in \ ]0,1[\) tel que \(f(c)=h=0\). Ce \(c\) satisfait \(f(c)=c^5+c-1=0\), il est donc solution de \(f(x)=0\). On remarque que la longueur de l'intervalle \([0,1]\) est \(1\).

Comme \(f\left(\frac{1}{2}\right)= \left(\frac{1}{2}\right)^5+\frac{1}{2}-1=\frac{-15}{32}\lt 0\), on peut maintenant considérer \(\left[\frac{1}{2},1\right]\), un intervalle de longueur \(\frac{1}{2}\). De nouveau par le TVI pour \(h=0\), il existe \(c\in \ \left]\frac{1}{2},1\right[\) tel que \(f(c)=h=0\).

On continue de cette manière pour réduire à chaque fois la longueur de l'intervalle dans lequel se trouve la solution \(c\). Ainsi, on obtient une bonne approximation de cette solution, sans la connaître exactement.

La preuve du TVI utilise la même idée d'un algorithme de bissection.

On remarque qu'on peut utiliser le TVI pour localiser un point d'intersection de deux courbes à un certain degré de précision. Si les deux courbes sont données par \(y=g(x)\) et \(y=h(x)\), alors on considère la fonction \(f(x)=g(x)-h(x)\) et on étudie les points où \(f(x)\) s'annule en utilisant le TVI.

Un polynôme de degré impair possède toujours une racine.

Considérons un polynôme de degré impair, \[ p(x)=a_{2n+1}x^{2n+1}+a_{2n}x^{2n}+a_{2n-1}x^{2n-1}+\cdots +a_0\,, \] avec \(a_{2n+1}\neq 0\).

Si \(a_{2n+1}\gt 0\), alors \(\lim_{x\rightarrow +\infty} p(x)=+\infty\) et \(\lim_{x\rightarrow -\infty} p(x)=-\infty\). On a donc \(M\gt 0\) tel que \(p(M)\gt 0\) et \(N\lt 0\) tel que \(p(N)\lt 0\). En appliquant le TVI sur l'intervalle \([N,M]\), on a qu'il existe \(c\in ]N,M[\) tel que \(p(c)=0\).

Si \(a_{2n+1}\lt 0\), alors \(\lim_{x\rightarrow +\infty} p(x)=-\infty\) et \(\lim_{x\rightarrow -\infty} p(x)=+\infty\), et on peut adapter le même argument.

Théorème: Soit \(f:[a,b]\to\mathbb{R}\) une fonction continue.

Considérons le premier cas, dans lequel \(f\) est strictement croissante. Dans ce cas, \(f(a)\leqslant f(x) \leqslant f(b)\) pour tout \(x\in [a,b]\), et donc \(\mathrm{Im} (f)\subset [f(a),f(b)]\). Puis, si on fixe une valeur intermédiaire \(h\), \(f(a)\lt h \lt f(b)\), le Théorème de la valeur intermédiaire garantit l'existence d'un \(x\in ]a,b[\) tel que \(f(x)=h\), ce qui implique que \(h\in\mathrm{Im} (f)\). Ainsi, \(]f(a),f(b)[\subset \mathrm{Im} (f)\). Puisque \(f(a),f(b)\in \mathrm{Im} (f)\), on a aussi \([f(a),f(b)]\subset \mathrm{Im} (f)\). On conclut donc que \(\mathrm{Im} (f)=[f(a),f(b)]\).

On sait maintenant que \(f:[a,b]\to \mathrm{Im} (f)\) est surjective. Mais étant strictement croissante, elle est également injective. Elle est donc bijective.

Dernière compilation: 2024-06-03 (22:36:08)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)