Analyse A (MAN) | G. Burmeister, S. Dubuis (EPFL)

Un ensemble est une collection bien définie d'objets/éléments distincts.

Souvent, on définit un ensemble \(E\) en listant les éléments qu'il contient:

Exemples:

\(E=\{\bigstar,\clubsuit,\spadesuit\}\). Notons que la façon dont les éléments sont listés n'importe pas: \(\{\bigstar,\clubsuit,\spadesuit\}\) et \(\{\spadesuit,\bigstar,\clubsuit\}\) définissent le même ensemble \(E\).
Ensembles contenant une infinité d'éléments: \[\begin{aligned} \mathbb{N}&=\{0,1,2,3,\dots\}\\ \mathbb{N}^*&=\{1,2,3,\dots\}\\ \mathbb{Z}&=\{\dots,-3,-2,-1,0,1,2,3,\dots\}\\ \mathbb{Q}&=\left\{\frac{p}{q}\,\big|\,p\in\mathbb{Z},q\in \mathbb{N}^*\right\} \end{aligned}\]

Exemple: L'ensemble des entiers positifs pairs est \[ E=\{2,4,6,8,\dots\}\,, \] et peut être décrit à l'aide d'une propriété, à savoir que c'est l'ensemble des entiers positifs \(x\) qui peuvent s'écrire comme un multiple de \(2\), c'est-à-dire pour lesquels il existe un entier \(k\) tel que \(x=2k\): \[ E=\{x\in \mathbb{N}\,|\,\exists k\in\mathbb{N}\,,x=2k\}\,. \]

On écrit ''\(x\in E\)'' pour indiquer que \(x\) est un élément de \(E\), ou que \(x\) appartient à \(E\). On écrira aussi ''\(x\not\in E\)'' pour indiquer que \(x\) n'est pas un élément de \(E\).
l'ensemble vide est l'ensemble ne contenant aucun élément. On le note \(\varnothing\). On a donc \(E\neq\varnothing\) si et seulement si \(\exists\, x\in E\) (\(E\) n'est pas vide si et seulement si il existe (au moins) un \(x\) dans \(E\)).
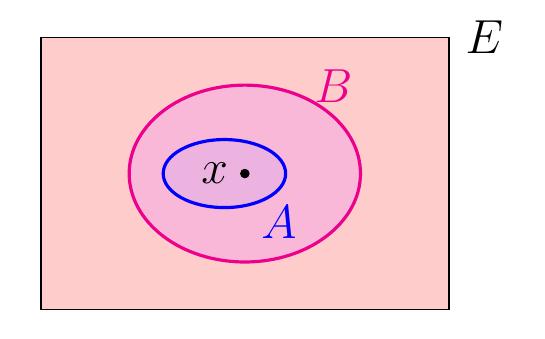
Inclusion: On dit qu'un ensemble \(A\) est un sous-ensemble de \(E\), et on note \(A\subset E\), si et seulement si \(\forall\, x\in A, x\in E\) (quel que soit \(x\) appartenant à \(A\), alors \(x\) appartient aussi à \(E\)).

Exemple: Si \(E=\{\bigstar,\clubsuit,\spadesuit\}\), alors

\(\clubsuit\in E\) mais \(\blacklozenge\not\in E\)
Si \(A=\{\clubsuit,\spadesuit\}\), alors \(A\subset E\).
Si \(B=\{\clubsuit,\blacklozenge\}\), alors \(B\not\subset E\).

Remarque: Il est important de faire attention avec l'usage des symboles ''\(\in\)'' et ''\(\subset\)''. Lorsqu'on parle d'un élément \(x \in E\), ce ''\(x\)'' est considéré comme un individu, alors que lorsqu'on écrit ''\(\{x\}\)'', on parle de l'ensemble contenant le seul élément \(x\). On écrit alors \(\{x\}\subset E\).

Exemples:

\( \mathbb{N}^\ast\subset \mathbb{N} \subset \mathbb{Q} \subset \mathbb{R} \)
\(\mathbb{Q} \not \subset \mathbb{N}\)
\(0\in \mathbb{N}\), \(0\not \in \mathbb{N}^*\)
\(-\frac32\not \in\mathbb{N}\), \(-\frac32\in\mathbb{Q}\)
\(\sqrt{2}\not \in \mathbb{Q}\), \(\sqrt{2}\in\mathbb{R}\)

Remarque:

Le symbole ''\(\subset\)'' ne représente pas forcément une inclusion stricte. Il est donc correct d'écrire ''\(A\subset A\)''.
L'inclusion est souvent utilisée pour caractériser l'égalité entre deux ensembles: \[ A=B \quad\Leftrightarrow\quad A\subset B \quad \text{et}\quad B\subset A\,. \]

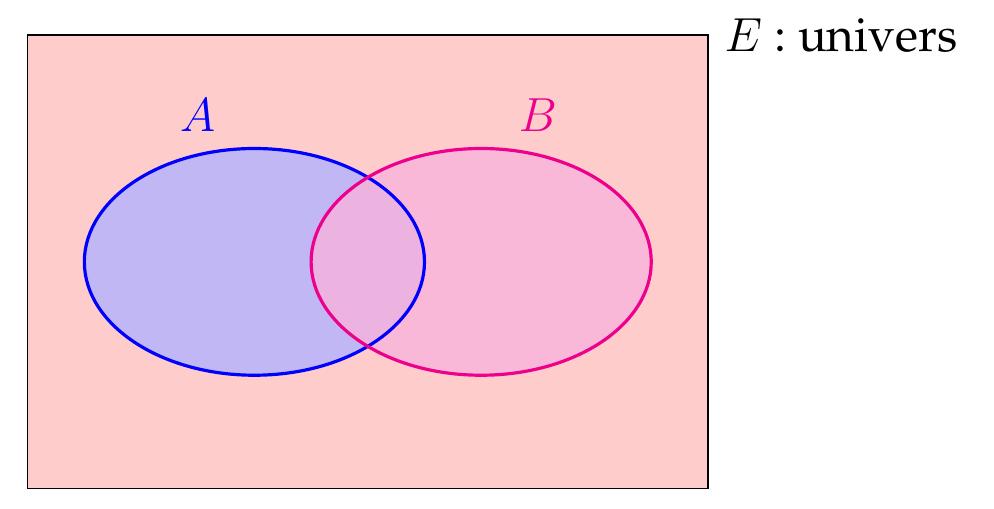
On travaille en général dans un ensemble de référence \(E\), non-vide, nommé univers, et on raisonne sur des sous ensembles de \(E\). On représente souvent des sous-ensembles \(A\subset E\) et \(B\subset E\) dans un diagramme de Venn:

Union, intersection

Rappelons quelques autres sous-ensembles de \(E\) qui peuvent être formés à l'aide d'ensembles donnés \(A\) et \(B\).

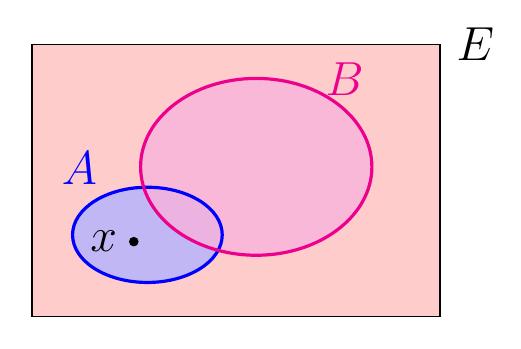
L'intersection de \(A\) et \(B\) est l'ensemble des éléments de \(E\) appartenant à \(A\) et à \(B\): \[ A\cap B = \{ x\in E \,|\, x\in A \text{ et }x\in B\}\,. \]
L'union de \(A\) et \(B\) est ensemble des éléments de \(E\) appartenant à \(A\) ou à \(B\) (ou aux deux, on dit que c'est un ''ou non-exclusif''): \[ A\cup B = \{ x\in E \,|\, x\in A \text{ ou }x\in B\}\,. \]

Exemple: Si \(A=\{\bigstar,\clubsuit,\spadesuit,\blacklozenge,0\}\), \(B=\{-1,0,\sqrt{2}\}\), alors

\(A\cap B=\{0\}\)
\(A\cup B= \{-1,0,\sqrt{2},\bigstar,\clubsuit,\spadesuit,\blacklozenge\}\).

Exemple: Si \(A=\left]-\infty,1\right]\), \(B=\left]0,2\right[\), \(C=\left]1,3\right]\), \(D=\left[3,4\right]\) alors

\(A\cap B=\left]0,1\right]\)
\(A\cap C=\varnothing\)
\(A\cup C=\left]-\infty,3\right]\)
\(B\cap C=\left]1,2\right[\)
\(B\cup C=\left]0,3\right]\)
\(A\cap D=\varnothing\)
\(B\cup D=\left]0,2\right[\cup \left[3,4\right]\) (pas de façon plus compacte de l'écrire!)
\(C\cap D= \{3\}\)

Exemples:

Si \(A=]0,1]\), \(B=[0,2]\), alors \(A\cap B=A\).
\(\mathbb{Q} \cap \mathbb{R}=\mathbb{Q}\)
\(\mathbb{N} \cap \mathbb{Q}=\mathbb{N}\)

Lorsqu'on prend l'union/intersection de plusieurs ensembles, on aura parfois recours à une notation indicielle semblable à celle utilisée pour les sommes et les produits. Plus précisément, pour une famille finie d'ensembles \(A_1,A_2,\dots,A_n\), on définit \[\begin{aligned} \bigcup_{k=1}^nA_k&=A_1\cup A_2\cup \cdots \cup A_n\,.\\ \bigcap_{k=1}^nA_k&=A_1\cap A_2\cap \cdots \cap A_n\,. \end{aligned}\] On a des notations semblables dans le cas de familles infinies (dites dénombrables): \[\begin{aligned} \bigcup_{k=0}^\infty A_k &= \bigcup_{k\in\mathbb{N}}A_k =A_0\cup A_1\cup A_2\cup \cdots \\ \bigcap_{k=0}^\infty A_k &= \bigcap_{k\in\mathbb{N}}A_k =A_0\cap A_1\cap A_2\cap \cdots \,, \end{aligned}\] ou encore \[\begin{aligned} \bigcup_{k\in\mathbb{Z}}A_k &=\cdots \cup A_{-1}\cup A_0\cup A_1\cup \cdots \\ \bigcap_{k\in\mathbb{Z}}A_k &=\cdots \cap A_{-1}\cap A_0\cap A_1\cap \cdots \,. \end{aligned}\]

Exemple: Si \(A_k=[k,k+1]\), alors \[\begin{aligned} \bigcup_{k\in \mathbb{N}}A_k &= [0,1]\cup [1,2]\cup [2,3]\cup\cdots =\mathbb{R}_+\,,\\ \bigcap_{k\in \mathbb{N}}A_k &= [0,1]\cap [1,2]\cap [2,3]\cap\cdots =\varnothing\,,\\ \bigcup_{k\in \mathbb{Z}}A_k &=\cdots\cup[-1,0]\cup [0,1]\cup [1,2]\cup\cdots =\mathbb{R}\,. \end{aligned}\]

Complémentaire

Parfois, lorsqu'il n'y a pas d'ambigüité sur l'univers \(E\), \(C_E(A)\) est aussi noté \(\overline{A}\) ou \(A^c\). On peut donc écrire que \[ \overline{\varnothing}=E\,,\qquad \overline{E}=\varnothing\,. \] On a toujours l'équivalence \[ x\not \in A \quad\Leftrightarrow\quad x\in \overline{A} \] Pour deux ensembles \(A,B\) quelconques, on définit aussi le complémentaire de \(A\) dans \(B\): \[ C_B(A)=\{x\in B \,|\, x\not\in A \} \]

Exemple: Si \(A=\{\bigstar,\clubsuit,\spadesuit\}\), \(B=\{\clubsuit,\spadesuit,\blacklozenge\}\), alors

\(A\cap B=\{\clubsuit,\spadesuit\}\)
\(A\cup B=\{\bigstar,\clubsuit,\spadesuit,\blacklozenge\}\)
\(C_A(B)=\{\bigstar\}\)
\(C_B(A)=\{\blacklozenge\}\)
\(C_A(A)=\varnothing\)

Exemples:

\(C_{\mathbb{N}}(\mathbb{N}^*)=\{0\}\)
\(C_{\mathbb{Z}}(\mathbb{N})=\{\dots,-3,-2,-1\}\)
\(C_{\mathbb{R}}(\mathbb{Q})=\) tous les nombres irrationnels

Lemme: Pour tous \(A,B\subset E\),

\(\overline{\overline{A}}=A\).
Si \(A\subset B\), alors \(\overline{B}\subset \overline{A}\).
\(\overline{A\cap B} = \overline{A}\cup \overline{B}\).
\(\overline{A\cup B} = \overline{A}\cap \overline{B}\).

Preuve:

Evident.
En effet, \[ x\in \overline{B} \quad\Leftrightarrow\quad x\not \in B \quad\Rightarrow\quad x\not \in A \quad\Leftrightarrow\quad x \in \overline{A} \]
En effet, \[\begin{aligned} x\in \overline{A\cap B} &\quad\Leftrightarrow\quad x\not\in A\cap B \\ &\quad\Leftrightarrow\quad x\not \in A \text{ ou } x\not \in B \\ &\quad\Leftrightarrow\quad x\in \overline{A} \text{ ou } x \in \overline{B} \\ &\quad\Leftrightarrow\quad x\in \overline{A}\cup \overline{B}\,. \end{aligned}\]
Pour y voir plus clair, posons \(\overline{A}=A'\), \(\overline{B}=B'\). Par le point précédent, on peut écrire \[\begin{aligned} \overline{\overline{A}\cap\overline{B}} &=\overline{A'\cap B'}\\ &=\overline{A'}\cup \overline{B'}\\ &=\overline{\overline{A}}\cup \overline{\overline{B}}\\ &=A\cup B\,. \end{aligned}\] Ainsi, \[ \overline{A}\cap \overline{B} =\overline{\overline{\overline{A}\cap \overline{B}}} =\overline{A\cup B}\,. \]

Dans un univers \(E\), \[\begin{aligned} A \subset B &\quad\Leftrightarrow\quad \forall\,x\in A,\, x\in B \\ &\quad\Leftrightarrow\quad A\cap\overline{B}=\varnothing \\ &\quad\Leftrightarrow\quad \overline{A} \cup B = E \end{aligned}\]

1.1 Notions de théorie des ensembles

Union, intersection

Complémentaire