Analyse A (MAN) | G. Burmeister, S. Dubuis (EPFL)

1.2 Propriétés et propositions

Introduction

En sciences, il est important de développer un langage univoque pour communiquer des faits et/ou analyser des résultats. Ce langage est celui de la logique mathématique. Voici quelques exemples :

Un résultat mathématique : le théorème de Pythagore. Pour tout triangle rectangle, la somme des carrés des cathètes est égale au carré de l'hypothénuse.
Une observation physique : sous les bonnes conditions, l'écoulement d'un fluide est régi par les équations de Navier-Stokes : \[ \rho \frac{\partial u }{\partial t} + \rho u\cdot \nabla u - \mu \Delta u + \nabla p = \rho f \]
Un projet en architecture : pour réduire les coûts environnementaux de construction de nouveaux bâtiments, on réutilise les matériaux d'anciens bâtiments qui ne sont plus en fonction.

Tous ces résultats, projets, observations s'expriment sous la forme de conditions, causes, buts qui impliquent un résultat, un modèle, une démarche.

Propriétés et ensembles

Une "phrase logique" se compose d'un objet ou d'un groupe d'objets, pris dans un référentiel sur lequel on applique une propriété. Le référentiel est l'ensemble des objets sur lesquels on définit des propriétés. Par exemple, la phrase "\(\sqrt{2}\) est irrationnel" se compose de

\(\sqrt{2}\) : un élément, ici un nombre réel pris dans le référentiel \(\mathbb{R}\).
La propriété "est irrationnel", appliquée à \(\sqrt{2}\).

Pour l'instant, nous avons juste construit une phrase, à prendre comme un assemblage de mots, sans se soucier de sa valeur de vérité, c'est-à-dire si elle est vraie ou fausse. Par exemple, on peut tout à fait écrire la phase "\(\sqrt{2}\) est rationnel". Il s'agira par la suite de déterminer s'il est correct d'affirmer "\(\sqrt{2}\) est rationnel".

Formellement, voici comment on peut écrire une propriété appliquée à un élément d'un référentiel.

Soit un référentiel \(E\) et \(P\) une propriété définie sur \(E\). La phrase "\(x\in E\) possède la propriété \(P\)" se note \(P(x)\). Cette écriture s'appelle le langage propositionnel.

Exemple: On choisit \(E=\mathbb{R}\). Soient \(P_1\) la propriété "est rationnel" et \(P_2\) la propriété est irrationnel".

La phrase "\(\sqrt{2}\) est rationnel" se note \(P_1(\sqrt{2}).\)
La phrase "\(\sqrt{2}\) est irrationnel" se note \(P_2(\sqrt{2}).\) .

Souvent, on écrit ces phrases dans le langage ensembliste, qui est un langage pratique pour effectuer des calculs logiques ou des raisonnements :

Exemple: Pour \(E=\mathbb{R}\).

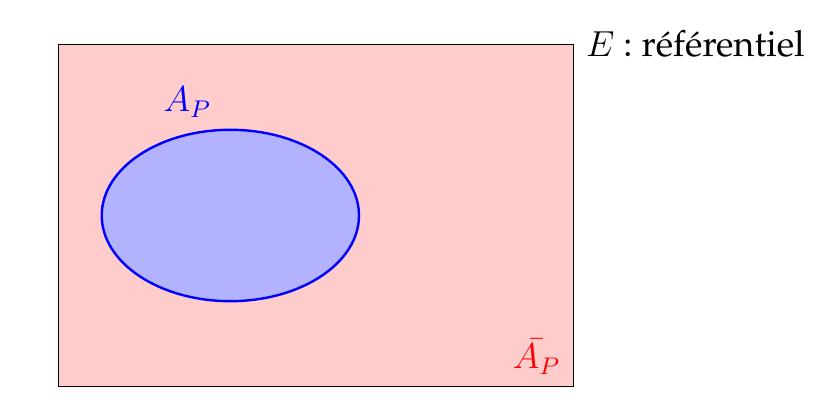
La phrase "\(\sqrt{2}\) est rationnel" se note \(\sqrt{2} \in \mathbb{Q}\).
La phrase "\(\sqrt{2}\) est irrationnel" se note \(\sqrt{2} \in \mathbb{R}\setminus \mathbb{Q}\).

Formellement, à toute propriété \(P\) définie sur \(E\), on peut associer un ensemble \(A_P\subset E\): \[A_P=\{x\in E \,|\, P(x) \}\ = \{x\in E \,|\, x \text{ possède la propriété }P \}\,.\] La phrase "\(x\) possède \(P\)" s'écrit alors comme \(x\in A_P\).

De même qu'on peut écrire la phrase "\(x\) possède la propriété \(P\)", on peut écrire la phrase "\(x\) ne possède pas la propriété \(P\)". La négation de la propriété \(P\) est notée \(\text{non}P\) et la phrase "\(x\) ne possède pas la propriété \(P\)" se note \(\text{non}P(x)\).

En langage ensembliste : \[A_{\text{non}P} = \{x\in E \,|\, \text{non}P(x) \}=C_{E}(A_P)=\bar{A}_P.\] \(\bar{A}_P\) est l'ensemble des \(x\) ne possédant pas la propriété \(P\). C'est le complémentaire de \(A_P\) dans \(E\).

En langage ensembliste, on utilise le diagramme de Venn pour représenter \(A_P\) et son complémentaire :

Considérons à présent une autre propriété \(Q\) définie sur \(E\) et \(A_Q\) son ensemble associé. Représentons la situation comme un diagramme de Venn :

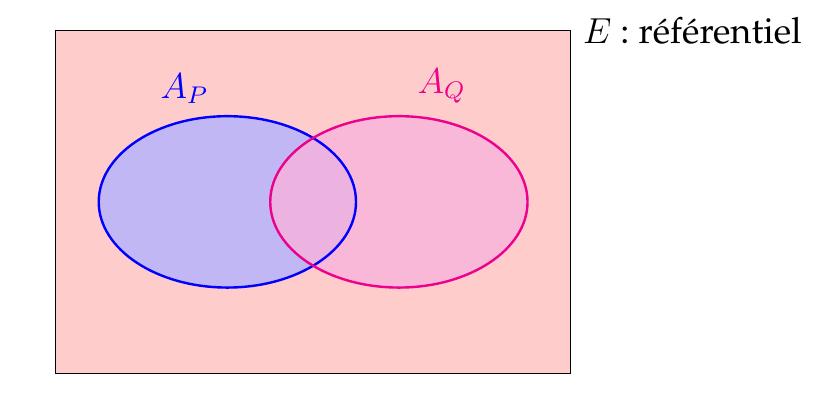
On peut combiner la propriété \(P\) avec \(Q\) :

\(x\) possède la propriété \((P\text{ et }Q)\), noté \((P\text{ et }Q)(x)\) ou \((P(x)\text{ et }Q(x))\), si \(x\) possède à la fois la propriété \(P\) et la propriété \(Q\). L'ensemble des \(x\) possèdant la propriété \((P\text{ et }Q)\) est \(A_{(P\text{ et }Q)}=A_P\cap A_Q\): \[A_{(P\text{ et }Q)}=A_P\cap A_Q=\{x\in E \,|\, P(x) \text{ et } Q(x) \}\,.\]
\(x\) possède la propriété \((P\text{ ou }Q)\), noté \((P\text{ ou }Q)(x)\) ou \((P(x)\text{ ou }Q(x))\), si \(x\) possède au moins l'une des deux propriétés (soit P, soit Q, soit les deux). L'ensemble des \(x\) possédant la propriété \((P\text{ ou }Q)\) est \(A_{(P\text{ ou }Q)}=A_P\cup A_Q\): \[A_{(P\text{ ou }Q)}=A_P\cup A_Q=\{x\in E \,|\, P(x) \text{ ou } Q(x) \}\,.\]
Négation de \(P\text{ et } Q\) : \(\text{non}\bigl(P\text{ et }Q\bigr)\) est \(\bigl(\text{non}P\text{ ou }\text{non}Q\bigr)\). En effet : \[\overline{A_P \cap A_Q} = \bar{A}_P\cup\bar{A}_Q \]
Négation de \(P\text{ ou }Q\): \(\text{non}\bigl(P\text{ ou }Q\bigr)\) est \(\bigl(\text{non}P\text{ et }\text{non}Q\bigr)\). En effet : \[\overline{A_P \cup A_Q} = \bar{A}_P\cap\bar{A}_Q\]

Remarque: On dit que \(P\) et \(Q\) sont incompatibles (elles ne peuvent pas être satisfaites simultanément) si et seulement si \(A_P \cap A_Q = \varnothing\).

Règles de calcul logique I:

\(\text{non}(P\text{ et }Q) = \text{non}P \text{ ou non}Q\)
\(\text{non}(P\text{ ou }Q) = \text{non}P \text{ et non}Q\)

Propositions

Soit \(P\) une propriété définie sur un référentiel \(E\) et \(A_P\) son ensemble associé correspondant.

Une proposition \(T\) est une affirmation énoncée à propos des éléments de \(E\).

On peut séparer les propositions en trois grandes familles.

Une proposition simple affirme qu'un élément particulier \(x_0\) de \(E\) possède la propriété \(P\): \[ T:\, P(x_0) \] En langage ensembliste, \(T:\, x_0\in A_P\).
Exemple: \(T\): \(\sqrt{2}\) est irrationnel.
Une proposition universelle affirme que tout \(x\) dans le référentiel \(E\) possède la propriété \(P\): \[ T:\, \forall\,x\in E,\, P(x) \] En langage ensembliste, \(T:\, A_P = E\).
Exemple: \(T:\forall x \in \mathbb{R}, x^2 \geqslant 0.\)
Une proposition existentielle affirme qu'au moins un élément de \(E\) possède la propriété \(P\) \[ T:\, \exists\,x\in E,\, P(x) \] En langage ensembliste, \(T:\,A_P \neq \varnothing\), ou encore \(T:\,\exists x\in E, x\in A_P\).
Exemple: \(T:\exists x \in \mathbb{R}, x^2=2.\)

Exprimons les négations de ces trois types de propositions:

Négation d'une proposition simple: \(x_0\) ne possède pas \(P\). \[ \text{non}T:\, \text{non}P(x_0) \] En langage ensembliste, \(\text{non}T\): \(x_0\not\in A_P\) ou encore \(x_0\in\bar{A}_P\).
Exemple: \(\text{non}T\): \(\sqrt{2}\) est rationnel.
Négation d'une proposition universelle: il existe \(x\in E\) t.q. \(x\) ne possède pas \(P\). \[\text{non}T:\, \exists\,x\in E,\, \text{non}P(x) \] En langage ensembliste, \(\text{non}T\): \(A_P \neq E\) ou encore \(\bar{A}_P \neq \varnothing\).
Exemple: \(\text{non}T:\exists x \in \mathbb{R}, x^2 <0.\)
Négation d'une proposition existentielle: quel que soit \(x\in E\), \(x\) ne possède pas \(P\). \[ \text{non}T:\, \forall\,x\in E,\, \text{non}P(x) \] En langage ensembliste, \(\text{non}T\): \(A_P=\varnothing\) ou encore \(\bar{A}_P = E\).
Exemple: \(\text{non}:\forall x\in\mathbb{R}, x^2 \neq 2.\)

À présent, on peut parler de valeur de vérité de l'affirmation \(T\): elle est soit vraie, soit fausse. Elle est vraie si et seulement si \(\text{non}T\) est fausse, et elle est fausse si et seulement si \(\text{non}{T}\) est vraie.

Remarque: Prendre garde à l'importance du référentiel: soit la propriété \(P(x):x^2=-1\). La proposition \[T:\exists x\in E, P(x)\] est fausse si \(E=\mathbb{R}\), mais vraie si \(E=\mathbb{C}\).

Règles de calcul logique II

\(\text{non}\left( \forall x \in E, P(x)\right)\) est \(\exists x \in E,\text{non}P(x)\)
\(\text{non}\left( \exists x \in E, P(x)\right)\) est \(\forall x \in E,\text{non}P(x)\)

Implications et équivalences

Un structure importante pour énoncer des résultats en sciences est l'implication. On observe un certain résultat si certaines conditions sont réunies.

Soient \(P\) et \(Q\) deux propriétés définies sur \(E\), \(A_P\) et \(A_Q\) les ensembles correspondants. L'affirmation "si \(x\) possède \(P\), alors \(x\) possède \(Q\)" s'écrit : \[P(x) \Rightarrow Q(x).\] On peut construire la proposition universelle : \[T:\forall x\in E, P(x) \Rightarrow Q(x).\] Souvent, on notera \(P\Rightarrow Q\) au lieu de \(T\).

En langage ensembliste, la proposition universelle \(P\Rightarrow Q\) exprime que tous les éléments de \(A_P\) sont aussi éléments de \(A_Q\): \[P\Rightarrow Q:\forall\,x\in A_P,\, x\in A_Q \] qui peut aussi s'écrire comme \[P\Rightarrow Q:\forall\,x\in E, \; \text{ si }x\in A_P,\, \text{ alors }x\in A_Q \] ou encore \[P\Rightarrow Q:A_P \subset A_Q.\]

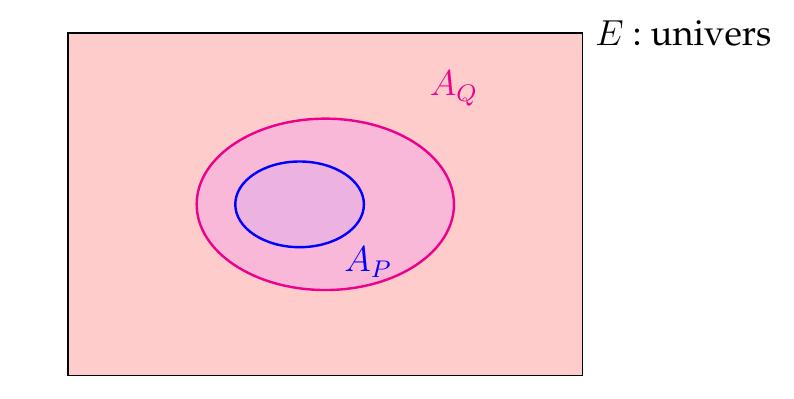
On constate que la condition \(P\) est plus restrictive que \(Q\). Tout \(x\) qui possède \(P\) possède nécessairement \(Q\), mais il y a des \(x\) qui peuvent posséder la propriété \(Q\) sans posséder la propriété \(P\).

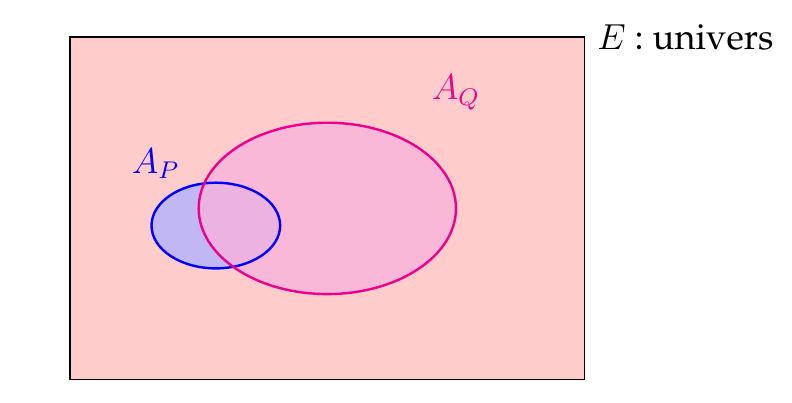
La proposition \(Q \Rightarrow P\) est appelée la réciproque de \(P\Rightarrow Q\). En langage ensembliste, on écrit \(Q \Rightarrow P:\forall\,x\in A_Q,\, x\in A_P \) ou encore \(A_Q \subset A_P\,.\)

On dit que \(P\) et \(Q\) sont équivalentes si et seulement si \(\bigl( P \Rightarrow Q \text{ et } P \Leftarrow Q\bigl)\), noté \(P \Leftrightarrow Q\).

En langage ensembliste, on aura \(\bigl( A_P \subset A_Q \text{ et } A_Q \subset A_P \bigl)\) c'est-à-dire \(\bigl( A_P=A_Q\bigl)\).

Le symbole \(\Leftrightarrow\) peut aussi s'utiliser pour comparer des propositions. Pour deux propositions \(T_1,T_2\), \(T_1 \Leftrightarrow T_2\) signifie que \(T_1\) et \(T_2\) sont équivalentes : elles partagent la même valeur de vérité. \(T_1\) est vraie si et seulement si \(T_2\) est vraie, et \(T_1\) est fausse si et seulement si \(T_2\) est fausse.

Il est important de savoir comment nier une implication. On a le résultat suivant : \[ \text{non}(\forall x\in E, P(x)\Rightarrow Q(x)) \Leftrightarrow \exists x \in E, P(x) \text{ et non}Q(x).\] En effet : \[\begin{aligned} \text{non}(\forall x\in E, P(x)\Rightarrow Q(x)) &\Leftrightarrow \text{non}\bigl( \forall\,x\in A_P,\, x\in A_Q )\\ &\Leftrightarrow A_P \not\subset A_Q \\ &\Leftrightarrow \exists\,x\in A_P,\, x\not\in A_Q \\ &\Leftrightarrow \exists\,x\in E,\,x\in A_P \text{ et } x\not\in A_Q \\ &\Leftrightarrow \exists\,x\in E,\, \bigl(P(x)\text{ et } \text{non}Q(x) \bigr)\,. \end{aligned}\]

La négation d'une implication est donc une proposition existentielle. A retenir :

Règles de calcul logique III:

\(\text{non}\left(\forall x \in E, P(x)\Rightarrow Q(x)\right) \Leftrightarrow \left( \exists x \in E, P(x) \text{ et non}Q(x)\right).\) Sous forme compacte : \(\text{non}(P\Rightarrow Q) \Leftrightarrow P \text{ et non}Q\).

Exemple: Un exemple important: la négation de la définition de limite. La définition de la limite d'une suite est: \[a_n \text{ converge vers } a \Leftrightarrow \lim_{n\rightarrow\infty} a_n = a\] \[\Leftrightarrow \] \[ \left(T:\, \forall\,\varepsilon>0,\, \exists\, N\in\mathbb{N} \text{ tel que } \forall n\in \mathbb{N}, \,n\geqslant N \Rightarrow |a_n-a|<\varepsilon\,\right). \] Considérons non("\(a_n\) converge vers \(a\)"). On va décomposer la proposition \(T\) et la nier par étape :

\(T: \forall \varepsilon >0, A(\varepsilon)\).
\(A(\varepsilon) : \exists N\in\mathbb{N}, B(N)\).
\(B(N) : \forall n\in\mathbb{N}, P(n) \Rightarrow Q(n)\).
\(P(n):n\geqslant N, \quad Q(n): \vert a_n -a \vert < \varepsilon.\)

On nie chaque partie indépendamment:

\(\text{non}T: \exists \varepsilon >0, \text{non}A(\varepsilon)\).
\(\text{non}A(\varepsilon) : \forall N\in\mathbb{N}, \text{non}B(N).\)
\(\text{non}B(N): \exists n \in \mathbb{N}, P(n) \text{ et } \text{non}Q(n).\)
\(\text{non}Q(n) : \vert a_n - a \vert \geqslant \varepsilon.\)

On récrit alors la négation bout à bout : \[\text{non}T: \exists \varepsilon>0, \forall N \in \mathbb{N}, \exists n \in \mathbb{N}, n\geqslant N \text{ et } \vert a_n-a\vert \geqslant \varepsilon.\]