Une théorie mathématique se construit sur des règles que l'on se donne au départ
(les axiomes et définitions)
et sur la logique. A partir des axiomes, on utilise le langage
logique pour déduire de nouveaux résultats, appelés propositions ou théorèmes.
Dans un référentiel, une proposition a une valeur de vérité:
elle est soit vraie, soit fausse.
Exemple: Sur le référentiel \(E=\mathbb{R}\), considérons les affirmations
Dans le but de montrer qu'une affirmation est vraie ou fausse, nous présenterons cinq méthodes de preuve:
Le but ici est de
montrer qu'une proposition universelle \(T:\forall x \in E ,
P(x)\Rightarrow Q(x)\) est vraie.
Pour un \(x\) quelconque, on montre que l'implication
\(P(x)\Rightarrow Q(x)\) est vraie en montrant que le contenu de \(P(x)\)
peut être utilisé directement, et développé de façon à impliquer
\(Q(x)\). Ceci se fait souvent en introduisant
une suite d'implications intermédiaires plus simples, toutes vraies:
\[\begin{aligned}
P(x)\Rightarrow \, & T_1(x)\\
&\Downarrow\\
& T_2(x)\\
&\Downarrow\\
&\,\, \vdots \\
&\Downarrow\\
&\,T_n(x)\,\Rightarrow Q(x)\,.
\end{aligned}\]
Les implications intermédiaires sont
introduites en détaillant naturellement les
éléments contenus dans l'affirmation de départ.
Exemple: Démontrons que l'affirmation de l'exemple du dessus, \(T\): ''le carré de tout entier pair est pair'', est vraie. Prenons un \(a\in\mathbb{Z}\), quelconque, et développons: \[\begin{aligned} a\text{ est pair} & \Rightarrow \exists\,k\in\mathbb{Z},\, a=2k \\ & \Rightarrow \exists\,k\in\mathbb{Z},\, a^2=(2k)^2=2\cdot \underbrace{2k^2}_{\in\mathbb{Z}} \\ & \Rightarrow \exists\,\ell\in\mathbb{Z},\, a^2=2\, \ell \\ & \Rightarrow \text{$a^2$ est pair}. \end{aligned}\] Ici, la première affirmation intermédiaire a seulement consisté à expliciter ce que signifie ''être pair'' (à savoir: pouvoir être écrit comme un multiple de \(2\)).
Le but ici est également de montrer qu'une proposition universelle est vraie, à l'aide de sa contraposée.
Exemple: La contraposée de la proposition ''s'il pleut, je sors avec mon parapluie'' est ''si je sors sans parapluie, c'est qu'il ne pleut pas''.
Remarquons
qu'une proposition est équivalente à sa contraposée:
\(T \Leftrightarrow C\).
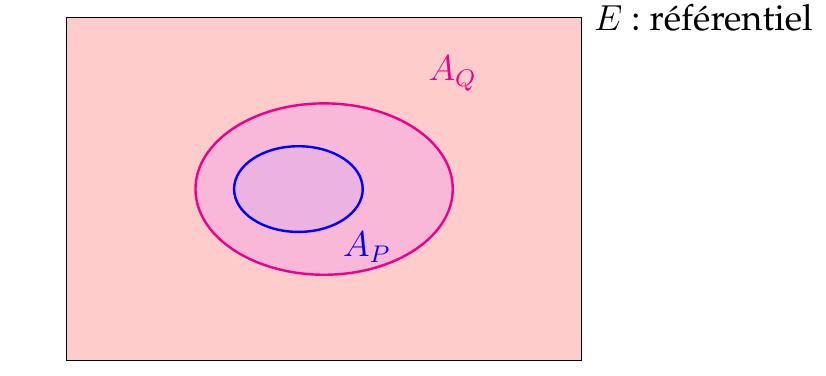
En langage ensembliste, cette équivalence s'écrit:
\[
A_P \subset A_Q
\qquad\Leftrightarrow\qquad
\overline{A_Q} \subset \overline{A_P}\,.
\]
( Tout
ce qui est dans \(A_P\) est aussi dans \(A_Q\) si et seulement si tout ce
qui n'est pas dans \(A_Q\) n'est pas non plus dans \(A_P\).
)

Comme \(T\) et sa contraposée sont équivalentes, on peut montrer que \(T\) est vraie en montrant que \(C\) est vraie, ce qui est parfois plus simple, comme dans l'exemple ci-dessous.
Exemple: Démontrons que
\[
T:\; \forall\,a\in \mathbb{Z}, \;\text{si $a^2$ est pair, alors $a$ est pair}
\]
est vraie. (Pas facile para la méthode directe, essayez!)
Ecrivons la contraposée de \(T\):
\[
C:\; \forall\,a\in\mathbb{Z}, \;\text{si $a$ est impair, alors $a^2$ est impair}\,,
\]
et montrons que \(C\) est vraie, par la méthode directe. Fixons
\(a\in\mathbb{Z}\). On a:
\[\begin{aligned}
\text{$a$ est impair}
& \Rightarrow \exists\,k\in\mathbb{Z},\, a=2k+1 \\
& \Rightarrow \exists\,k\in\mathbb{Z},\, a^2=(2k+1)^2=2\cdot ( \underbrace{2k^2+2k}_{\in\mathbb{Z}}) +1 \\
& \Rightarrow \exists\,\ell\in\mathbb{Z},\, a^2=2\, \ell+1 \\
& \Rightarrow \text{$a^2$ est impair}.
\end{aligned}\]
Donc \(C\) est vraie, et donc \(T\) est vraie également.
Remarque: Ne pas confondre la contraposée avec la négation et la réciproque! En effet, rappelons que pour une affirmation universelle \(T:\) \(\forall x\in E\), \(P(x)\Rightarrow Q(x)\), on a
Remarquons pour commencer qu'en toute généralité, une affirmation est fausse
(resp. vraie) si
et seulement si sa négation est vraie (resp. fausse).
Le but ici est de montrer qu'une proposition universelle
\[
T:\,\forall x\in E,\, P(x)
\]
est fausse en montrant que sa négation est vraie.
Or pour montrer que
\[
\text{non}T:
\exists x_0\in E,\, \text{non}P(x_0)
\]
est vraie, il suffit d'exhiber un \(x_0\in E\) qui ne satisfait pas \(P\);
ce \(x_0\) est appelé contre-exemple.
Exemple: Par ce qu'on a vu dans un exemple précédent, la proposition
\[
T:\forall a\in \mathbb{Z},
a^2 \text{ pair }
\Rightarrow
a \text{ impair }
\]
est fausse. Mais une autre façon de montrer que \(T\)est fausse est de
considérer sa négation,
\[\text{non}T :
\exists a_0\in\mathbb{Z}, a_0^2
\text{ pair et }
a_0
\text{ pair}\,.
\]
et de remarquer que
\(\text{non}T\) est vraie, puisqu'en prenant \(x_0=2\), on a
\(x_0^2=4\) et \(2\) est pair.
Remarquons pourtant que:
Exemple:
Considérons
l'affirmation \(T\): toute suite réelle \(x_n\) dont le carré
\({x_n}^2\) converge est elle-même convergente
.
Montrons que \(T\) est fausse, en considérant sa négation \(\text{non} T\):
il existe une suite \(x_n\) divergente telle que \({x_n}^2\) converge
.
Comme contre-exemple, il suffit de
prendre \(x_n=(-1)^n\), qui est divergente, alors que son
carré \({x_n}^2=+1\) est une suite constante, et donc convergente.
Exemple:
Considérons l'affirmation \(T\): la somme de deux irrationnels est
irrationnelle
.
Sa négation est \(\text{non}T\): il existe deux irrationnels dont la somme
est rationnelle
, et elle est vraie puisqu'on peut par exemple
prendre \(x=-\sqrt{2}\) et \(y=\sqrt{2}\)
sont tous deux irrationnels, mais leur somme \(x+y=0\) est rationnelle. Donc
\(T\) est fausse.
On a déjà dit qu'une façon de montrer
qu'une proposition \(T\) est vraie est de montrer que sa
négation, \(\text{non}T\), est fausse.
L'idée de la méthode de preuve par l'absurde est la suivante:
on montre que \(\text{non}T\) est fausse en montrant qu'elle ne peut pas être
vraie, dans le sens suivant: supposer que \(\text{non}T\) est vraie mène à une
conclusion absurde, en contradiction avec les hypothèses de départ.
Remarquons que de manière très générale, une proposition peut toujours
s'écrire sous la forme d'une implication, \(T:H\Rightarrow C\), qui comporte
Pour montrer qu'une implication
\[
T:H\Rightarrow C
\]
est
vraie, la méthode consiste à montrer que si \(\text{non}T\) est vraie, alors on
arrive à une contradiction. Dit encore autrement, puisque
\[
\text{non }T: H \text{ et non }C\,,
\]
on démontre que sous les hypothèses \(H\),
\(\text{non} T\) est impossible car en contradiction avec \(H\).
Voyons un exemple classique.
Exemple: Montrons que l'affirmation \(\sqrt{2}\) est irrationnel
, c'est-à-dire
\[
T:\,\sqrt{2}\not\in \mathbb{Q}\,,
\]
est vraie. Pour la démontrer par l'absurde, on considère
\[
\text{non T}: \sqrt{2} \in \mathbb{Q}\,.
\]
Si \(\text{non} T\) est vraie, cela signifie que l'on
peut choisir \(a,b\in \mathbb{N}^*\) tels que
\[\frac{a}{b}=\sqrt{2}\,.
\]
Remarquons que l'on peut supposer que la fraction \(\frac{a}{b}\) est
irréductible, c'est-à-dire que \(a\) et \(b\) n'ont aucun diviseur en commun.
Ensuite, élevons \(\frac{a}{b}=\sqrt{2}\) au carré, pour obtenir
\[
\frac{a^2}{b^2}=2
\quad \Leftrightarrow \quad
a^2 = 2b^2.
\]
Ceci implique que \(a^2\) est pair.
Par ce que nous avions montré plus haut, cela implique
que \(a\) est pair, et donc qu'il peut s'écrire comme
\(a=2c\) pour un certain \(c\in \mathbb{Z}\).
Donc on a finalement que
\[a^2=(2c)^2=4c^2 = 2b^2
\quad \Rightarrow \quad
2c^2 = b^2.
\]
Donc \(b^2\) est pair, et ceci implique que \(b\) est pair à son tour. Donc
\(b=2d\) pour un certain \(d\in\mathbb{N}\). Donc on en déduit que \(a\) et \(b\) sont
pairs tous les deux, et donc qu'ils ont un diviseur commun: \(2\).
Ceci est en contradiction avec notre hypothèse de départ.
Par conséquent, \(\text{non}T\) ne peut pas être vraie, elle est donc fausse, et
\(T\) est vraie: \(\sqrt{2}\) est irrationnel.
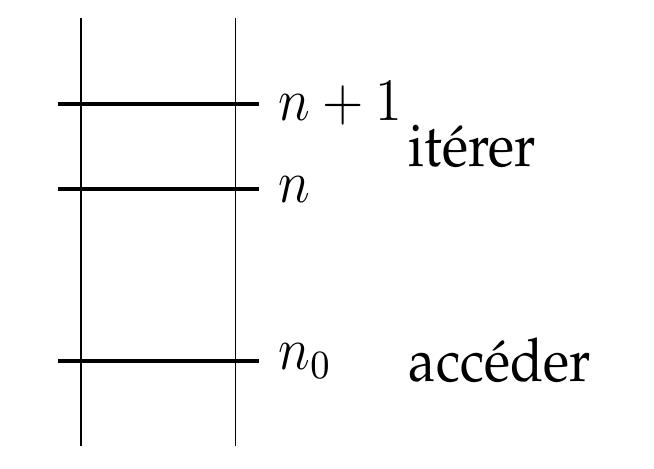
But: montrer qu'une proposition \(P(n)\) dépendant d'un entier positif \(n\) est vraie pour tout \(n\) à partir d'une valeur \(n_0\): \[\forall\,n\geqslant n_0,\, P(n) \text{ vraie}.\] L'idée est la suivante. Imaginons un petit bonhomme qui doit gravir un escalier infiniment haut. Quelles sont les facultés qu'il doit posséder?
Exemple: Soit \(S_n\) définie par \[S_n= 1\cdot 1! + 2\cdot 2! + 3\cdot 3! + \cdots + n\cdot n! = \sum_{k=1}^n k\cdot k!\,.\] Démontrer \[\forall\,n\in\mathbb{N}^\ast,\, S_n=(n+1)!-1\,.\] Notons \(P(n):\, S_n=(n+1)!-1\).