5.2 Logarithme
On définit le logarithme naturel
\(\ln : \mathbb{R}^{*}_+ \rightarrow \mathbb{R}\) par
\[\ln(x) = \int_1^x \frac{1}{t}\,dt.\]
Géométriquement, \(\ln(x)\) représente l'aire algébrique de la portion du plan
délimité par le graphe de \(f(t)=\frac{1}{t}\) et les droites \(t=1,t=x,y=0.\)
De par sa définition,
- \(\ln(1)=0\)
- \(\ln(x) \gt 0 \Leftrightarrow x\gt 1\)
- \(\ln(x) \lt 0 \Leftrightarrow x\lt 1\)
Le logarithme étant défini comme la fonction-aire associée à
\(f(t)=\frac{1}{t}\), le Théorème Fondamental
de l'Analyse garantit
qu'il est dérivable sur \(]0,+\infty[\), et qu'en plus
\[\ln'(x) =
\left(
\int_1^x \frac{1}{t}\,dt
\right)'
=
\frac{1}{x}\,.\]
En particulier, \(\ln(x)\) est strictement croissante, puisque sa dérivée
est \(\frac{1}{x}\gt 0\) pour tout \(x\gt 0\).
La propriété fondamentale
La propriété la plus importante du logarithme est de transformer des
produits en sommes:
Théorème:
Si \(x,y\gt 0\), alors
\[
\ln(x\cdot y) = \ln(x) + \ln(y)\,.
\]
Preuve:
Fixons \(x,y\gt 0\).
En utilisant la relation de Chasles,
\[\begin{aligned}
\ln(x\cdot y) - \ln(y)
&=\int_{1}^{xy} \frac{1}{t}dt - \int_{1}^{y} \frac{1}{t} dt \\
&= \int_{y}^{xy} \frac{1}{t}dt\,.
\end{aligned}\]
Introduisons la nouvelle variable \(u=t/y\), qui donne \(dt=y\,du\), et donc
\[
\int_{y}^{xy} \frac{1}{t}dt
= \int_{1}^x \frac{1}{uy}y\,du
= \int_{1}^x \frac{1}{u}du
= \ln(x)\,,
\]
et donc la formule est démontrée.
Remarquons que l'opération qui transforme
\(\int_1^x\frac{1}{t}\,dt\)
en
\(\int_y^{yx}\frac{1}{t}\,dt\)
correspond à un "glissement" de la portion du plan sous la
courbe entre \(1\) et \(x\):
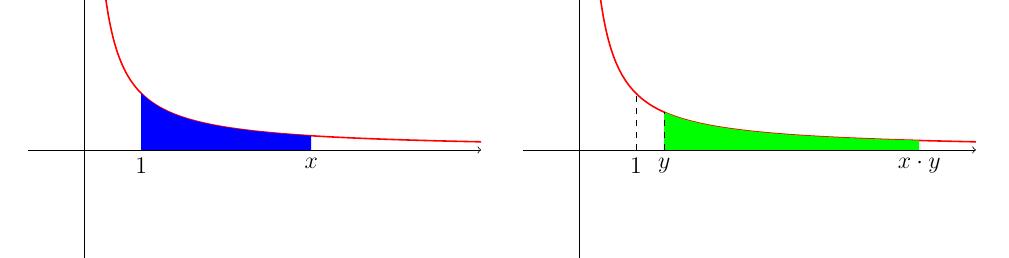
Le changement de variable que l'on a opéré dans l'intégrale correspond à
appliquer à l'aire bleue la transformation
\[
T_y:\mathbb{R}^2 \to \mathbb{R}^2\,,
\]
qui a tout couple \((a,b)\) fait correspondre le couple
\((ya, \frac{b}{y})\).
Par exemple le couple \((1,1)\) est envoyé sur
\((y,1/y)\), et \((x,1/x)\) est envoyé
sur \((yx,1/yx)\). On peut montrer que cette
transformation préserve les aires, puisqu'elle
est linéaire et que sa matrice relativement à la
base canonique est donnée par
\[ \begin{pmatrix}
y & 0 \\ 0 &\frac{1}{y}
\end{pmatrix}
\]
dont le déterminant vaut \(1\).
L'aire bleue est égale à \( \ln(x)\), l'aire verte vaut \(\ln(xy)-\ln(y)=\)(aire
entre \(xy\) et 1)-(aire entre \(y\) et 1). Le calcul intégral plus haut revient
à montrer que ces aires sont égales.
On conclut de la propriété précédente :
- \(\forall x\gt 0\),
\(\ln\left(\frac{1}{x}\right) =-\ln(x)\)
- \(\forall x,y\gt 0\),
\(\ln\left(\frac{x}{y}\right) = \ln(x)-\ln(y)\)
- \(\forall x\gt 0\), \(\forall n\in\mathbb{N},\) \(\ln(x^n)=n\ln(x)\).
Preuve:
- Si \(x\gt 0\),
\[
0=\ln(1)
=\ln\left(x \cdot \frac{1}{x}\right)
=\ln(x)+\ln\left(\frac{1}{x}\right)\,,
\]
et donc
\( \ln\left(\frac{1}{x}\right) =-\ln(x)\)
-
\(
\ln\left(\frac{x}{y}\right)
=\ln\left( x \cdot \frac{1}{y}\right)
=\ln(x)+\ln\left(\frac{1}{y}\right)
=\ln(x)-\ln(y)
\)
- La propriété est vérifiée
pour \(n=2\), puisque
\[
\ln(x^2)=\ln(x\cdot x)=\ln(x)+\ln(x)=2\ln(x)\,.
\]
Si elle est vraie pour \(n\), alors
\[
\ln(x^{n+1})=\ln(x^n\cdot x)=
\ln(x^n)+\ln(x)
=n\ln(x)+\ln(x)=(n+1)\ln(x)\,,
\]
donc elle est vraie aussi pour \(n+1\).
La dernière propriété s'étend à des puissances négatives \(n\lt 0\). En effet,
si \(n=-m\), \(m\in \mathbb{N}\), alors
\[\begin{aligned}
\ln(x^{n})
=\ln(x^{-m})
= \ln\left(\frac{1}{x^m}\right)
&=-\ln(x^m) \\
&= (-m)\ln(x)
= n\ln(x)\,.
\end{aligned}\]
Elle s'étend également à des exposants rationnels;
on retiendra la règle de calcul:
pour tout \(\alpha\in \mathbb{Q}\),
\[\ln(x^\alpha) = \alpha\ln(x)\,,\quad x\gt 0\]
Injectivité
Puisque \(\ln:\mathbb{R}_+^*\to \mathbb{R}\)
est strictement croissante, elle est injective.
On a donc les équivalences suivantes, utiles pour la résolution
d'équations/inéquations: pour tout \(u,v\gt 0\),
\[\begin{aligned}
\ln(u)=\ln(v)
&\quad\Leftrightarrow\quad
u=v \\
\ln(u) \lt \ln(v)
&\quad\Leftrightarrow\quad
u \lt v\\
\ln(u) \leqslant \ln(v)
&\quad\Leftrightarrow\quad u \leqslant v
\end{aligned}\]
Exemple:
Résolvons
\[
\ln(x+1)+\ln(x+2)=\ln(2)
\]
Les logarithmes sont bien définis lorsque
\(x\in D_{\text{déf}}\), où
\[
D_{\text{déf}}
=\{x\in \mathbb{R}\,|\,x+1\gt 0\text{ et }x+2\gt 0\}
=]-1,+\infty[\,.
\]
Sur \(D_{\text{déf}}\),
\[\begin{aligned}
\ln(x+1)+\ln(x+2)=\ln(2)
&\iff \ln\left((x+1)(x+2)\right)=\ln(2)\\
&\iff (x+1)(x+2)=2\\
&\iff x(x+3)=0\,,
\end{aligned}\]
et donc
\[
S=D_{\text{déf}}\cap\{0,-3\}=\{0\}\,.
\]
Exemple:
Résolvons
\[ 2\ln(x)\gt \ln(x+2)\,.
\]
Notons d'abord que les deux deux membres de l'inégalité sont bien définis
lorsque \(x\in D_{\text{déf}}\), où
\[D_{\text{déf}}=\{x\in \mathbb{R}\,|\,x\gt 0\text{ et }x+2\gt 0\}
=]0,+\infty[\,.
\]
Sur \(D_{\text{déf}}\), on a maintenant
\[\begin{aligned}
2\ln(x)\gt \ln(x+2)
&\iff \ln(x^2)\gt \ln(x+2)\\
&\iff x^2\gt x+2\\
&\iff x^2- x-2\gt 0\\
&\iff (x+1)(x-2)\gt 0\,.
\end{aligned}\]
L'ensemble solution est donc
\[\begin{aligned}
S
&=D_{\text{déf}}\cap\left(]-\infty,-1[\cup]2,\infty[\right)\\
&=]2,\infty[\,.
\end{aligned}\]
Exemple:
Résolvons
\[ \ln(x^2)\gt \ln(x+2)\,.
\]
Notons d'abord que les deux deux membres de l'inégalité sont bien définis
lorsque \(x\in D_{\text{déf}}\), où
\[D_{\text{déf}}=\{x\in \mathbb{R}\,|\,x\neq 0\text{ et }x+2\gt 0\}
=]-2,0[\cup]0,+\infty[\,.
\]
Sur \(D_{\text{déf}}\), on a maintenant
\[\begin{aligned}
\ln(x^2)\gt \ln(x+2)
&\iff x^2\gt x+2\\
&\iff (x+1)(x-2)\gt 0\,.
\end{aligned}\]
L'ensemble solution est donc
\[
S
=D_{\text{déf}}\cap\left(]-\infty,-1[\cup]2,\infty[\right)
=]-2,-1[\cup ]2,\infty[\,.
\]
Surjectivité
On a dit plus haut que \(\ln(x)\) est strictement croissante, mais ceci ne dit
pas quel est son comportement lorsque \(x\to+\infty\) ou \(x\to 0^+\).
Lemme:
\(\ln:\mathbb{R}_+^*\to \mathbb{R}\) n'est pas majorée, car
\[
\lim_{x\rightarrow + \infty} \ln(x) = +\infty\,,
\]
et pas minorée, car
\[
\lim_{x\rightarrow 0^{+}} \ln(x) = -\infty\,.
\]
Preuve:
En termes géométriques, la limite
\[
\lim_{x\rightarrow + \infty} \ln(x)
\]
représente l'aire de la région sous le graphe de \(f(t)=\frac1t\), entre \(t=1\)
et l'infini.
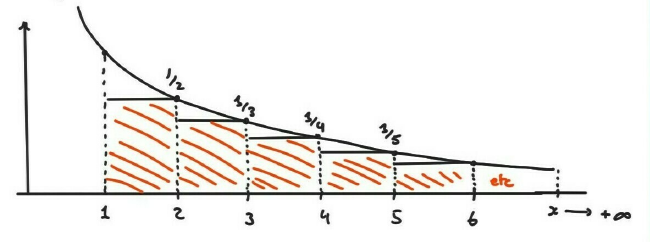
Considérons une famille infinie
de rectangles, tous de largeur égale à
\(1\), situés sous le graphe de \(f(t)=\frac{1}{t}\):
L'aire du \(k\)ème rectangle, dont la base est l'intervalle \([k,k+1]\), a une
aire égale à \(1\cdot \frac{1}{k+1}\).
Puisque tous ces rectangles sont sous le graphe,
\[
\lim_{x\rightarrow + \infty} \ln(x)
\geqslant
\frac12+\frac13+\frac14+\frac15+\frac16+\frac17+\frac18+\frac19+\frac1{10}+\cdots
\]
(Cette somme infinie est appelée la
série harmonique.)
On groupe les termes de la somme en paquets, comme suit:
\[\begin{aligned}
&\left(
\frac12
\right)\\
+&
\left(
\frac13+\frac14
\right)\\
+&
\left(
\frac15+\dots+\frac18
\right)\\
+&
\left(
\frac19+\cdots+\frac{1}{16}
\right)\\
+&\cdots\\
+&
\left(
\frac{1}{2^{k-1}+1}+\cdots+\frac{1}{2^k}
\right)\\
+&\cdots
\end{aligned}\]
On remarque que la somme que représente le \(2\)ème paquet peut être minorée
comme suit:
\[
\frac13+\frac14
\geqslant
\frac14+\frac14
=
2\cdot \frac14
=\frac{1}{2}
\]
Pour le troisième paquet, qui contient \(4\) termes,
\[\begin{aligned}
\frac15+\dots+\frac18
&= \frac15+\frac16+\frac17+\frac18\\
&\geqslant \frac18+\frac18+\frac18+\frac18\\
&=4\cdot \frac{1}{8}
=\frac12
\end{aligned}\]
On peut faire de même pour
le \(k\)ème paquet: c'est une somme de \(2^{k-1}\) termes, et comme chaque terme
est plus grand que le dernier du paquet,
\[\begin{aligned}
\frac{1}{2^{k-1}+1}+\cdots+\frac{1}{2^k}
&\geqslant
\frac{1}{2^{k}}+\cdots+\frac{1}{2^k}\\
&=2^{k-1}\cdot \frac{1}{2^k}=\frac12\,.
\end{aligned}\]
Ceci montre que la somme totale est plus grande qu'une somme d'une infinité de
paquets. Comme chaque paquet représente une somme d'au moins \(\frac12\), ceci
montre que
\[
\frac12+\frac13+\frac14+\frac15+\frac16+\frac17+\frac18+\frac19+\frac1{10}+\cdots=
+\infty\,,
\]
et donc que
\[
\lim_{x\rightarrow + \infty} \ln(x) =+\infty
\]
Pour la deuxième limite, le changement de variable \(x=\frac{1}{s}\) implique
\[
\lim_{x\to 0^+}\ln(x)
=
\lim_{s\to +\infty}\ln\left(\frac{1}{s}\right)
=
-\lim_{s\to +\infty}\ln(s)
=-\infty\,.
\]
Comme \(\ln:\mathbb{R}_+^*\to \mathbb{R}\) est dérivable, elle est continue. Les limites au
borne du domaine \(\mathbb{R}_+^*\), dans le lemme ci-dessus, et le Théorème des valeurs
intermédiaires, impliquent que \(\mathrm{Im} (\ln)=\mathbb{R}\).
On en conclut que \(\ln\) est surjective.
En particulier,
il existe un nombre \(x\) tel que \(\ln(x)=1\). On note
ce nombre \(e\).
Exemple:
Résolvons l'inéquation
\[
\ln(1-x) + \ln(x) \leqslant 2\,.
\]
Commençons par le domaine de définition: pour que \(\ln(1-x)\) et \(\ln(x)\)
soient bien définis, il faut que \(1-x\) et \(x\) soient simultanément dans le
domaine du logarithme:
\[ D_{\text{déf}}
= \left\{x\in\mathbb{R} | 1-x\gt 0 \text{ et } x\gt 0 \right\}
= ]0,1[\,.
\]
Sur \(D_{\text{déf}}\),
\[\begin{aligned}
\ln(1-x) + \ln(x) \leqslant 2
& \quad\Leftrightarrow\quad \ln((1-x)x) \leqslant 2\cdot 1 \\
& \quad\Leftrightarrow\quad \ln((1-x)x) \leqslant 2 \ln(e) \\
& \quad\Leftrightarrow\quad \ln((1-x)x) \leqslant \ln(e^2) \\
& \quad\Leftrightarrow\quad (1-x)x \leqslant e^2 \\
&\quad\Leftrightarrow\quad x^2 -x + e^2 \geqslant 0 \,.
\end{aligned}\]
Puisque \(\Delta=(-1)^2-4e^2\lt 0\) et puisque
le coefficient devant \(x^2\) est \(1\gt
0\), on a que tout \(x\in D_{\text{déf}}\) est solution.
Donc \(S=D_{\text{déf}}=]0,1[\).