5.4 Base quelconque

L'exponentielle et le logarithme des deux dernières sections permet de généraliser la notion de puissance à des exposants réels (jusqu'à présent, nous pouvions comprendre \(a^p\) avec \(p\in\mathbb{Q}\) mais pas \(a^x\) avec \(x\) un irrationnel).

Soit \(a\gt 0\). On définit l'exponentielle de base \(a\) comme la fonction \[\begin{aligned} \exp_a:\mathbb{R}& \to \mathbb{R}\\ x& \mapsto \exp_a(x)=\exp(x\ln(a)) \end{aligned}\]

De par sa définition, \(\exp_a\) hérite des mêmes propriétés que \(\exp\). On a par exemple la propriété fondamentale: \[ \exp_a(x+y)=\exp_a(x)\cdot \exp_a(y)\,. \] Ceci implique pour tout entier \(n\), \(\exp_a(n)=a^n\), et donc nous mène à utiliser la notation suivante: \[ a^x:= \exp_a(x)\,. \] L'exponentielle de base \(a\) est également dérivable, et \[ (a^x)' =\left(\exp(x\ln(a))\right)' =\exp(x\ln(a))\left(x\ln(a)\right)' =\underbrace{a^x}_{\gt 0}\ln(a)\,. \] Ainsi,

  1. si \(0\lt a\lt 1\), alors \(\ln(a)\lt 0\) et \(a^x\) est strictement décroissante,
  2. si \(a=1\), alors \(\ln(a)=0\) et \(a^x\) est constante (égale à \(1\)),
  3. si \(a\gt 1\), alors \(\ln(a)\gt 0\) et \(a^x\) est stricement croissante.

Sur l'animation ci-dessous, on observe ce changement de monotonicité en faisant varier la base \(a\):

Remarquons que \[\lim_{x\rightarrow +\infty} a^x = \left\{\begin{array}{c} +\infty, \quad a\gt 1 \\ 0, \quad a\lt 1 \end{array}\right.\] \[\lim_{x\rightarrow -\infty} a^x = \left\{\begin{array}{c} 0, \quad a\gt 1 \\ +\infty, \quad a\lt 1 \end{array}\right.\]

Logarithme en base \(a\gt 0\)

Pour une base \(a\gt 0\), différente de \(1\), la fonction \(\exp_a:\mathbb{R}\to\mathbb{R}^*_+\) est bijective. Elle admet donc une réciproque:

Pour une base \(a\gt 0\), \(a\neq 1\), la réciproque de \(\exp_a:\mathbb{R}\to\mathbb{R}^*_+\) est appelée logarithme en base \(a\): \[\begin{aligned} \log_a : \mathbb{R}^{*}_+ &\rightarrow \mathbb{R} \\ x &\mapsto y = \log_a(x) \end{aligned}\]

On a donc, par définition, \[ a^x=y \quad \Leftrightarrow \quad x=\log_a(y) \]

Par construction (il est la réciproque d'une fonction de type exponentielle), le logarithme de base \(a\) partage les propriétés et les règles de calcul du logarithme naturel. En particulier \(\log_a(1) =0\) et \(\log_a(a) =1\).

On peut en fait toujours l'exprimer à l'aide de \(\ln\):

\(\forall a\gt 0\), \(a\neq 1\), \[ \log_a(x) =\frac{\ln(x)}{\ln(a)}, \qquad\forall x \gt 0\,. \]

Si \(y=\log_a(x)\), alors \[\begin{aligned} y=\log_a(x) &\quad\Leftrightarrow\quad a^y = x \\ &\quad\Leftrightarrow\quad e^{y\ln(a)} = e^{\ln(x)} \\ & \quad\Leftrightarrow\quad y\ln(a) = \ln(x)\\ &\quad\Leftrightarrow\quad y = \frac{\ln(x)}{\ln(a)} \end{aligned}\]

On a en particulier que \[ \left(\log_a(x) \right)' =\left(\frac{\ln(x)}{\ln(a)}\right)' = \frac{1}{\ln(a)}\frac{1}{x}\,. \] Donc

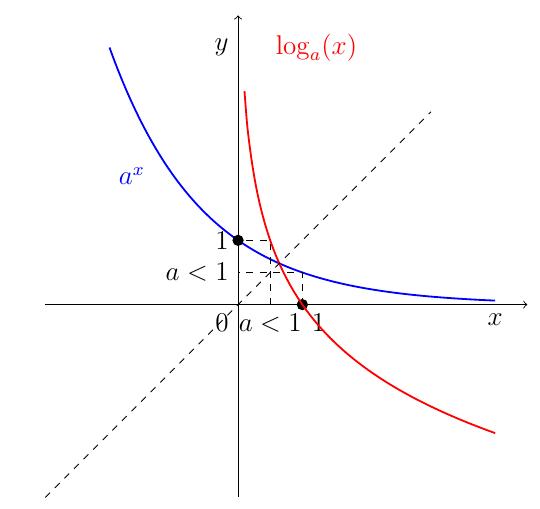
Le graphe de \(\log_a\) s'obtient par symétrie d'axe \(x=y\) à partir du graphe de \(a^x\) (en gris):

On observe en particulier que \[\lim_{x\rightarrow +\infty} \log_a(x) = \left\{\begin{array}{c} +\infty, \quad a\gt 1 \\ -\infty, \quad a\lt 1 \end{array}\right.\] \[\lim_{x\rightarrow 0^{+}} \log_a(x) = \left\{\begin{array}{c} -\infty, \quad a\gt 1 \\ +\infty, \quad a\lt 1 \end{array}\right.\]

Exemple: Soit \(a\in\mathbb{R}^{*}_+\setminus\{1\}\). Résolvons \[ \log_a(x) + \log_a(x-2a) \geqslant 2 + \log_a(3)\,. \] La base \(a\) joue donc le rôle d'un paramètre.

Commençons par \[ D_{\text{déf}} = \left\{x\in\mathbb{R} | x\gt 0 \text{ et } x-2a\gt 0\right\} = ]2a,+\infty [\,. \] Sur \(D_{\text{Déf}}\), \[\begin{aligned} \log_a(x) + \log_a(x-2a) &\geqslant 2 + \log_a(3) \\ &\Leftrightarrow \log_a(x(x-2a)) \geqslant 2\cdot 1 + \log_a(3) \\ &\Leftrightarrow \log_a(x(x-2a)) \geqslant 2\log_a(a) + \log_a(3) \\ &\Leftrightarrow \log_a(x(x-2a)) \geqslant \log_a(a^2)+ \log_a(3) \\ &\Leftrightarrow \log_a(x(x-2a)) \geqslant \log_a(3a^2) \end{aligned}\] On distingue à présent les cas:

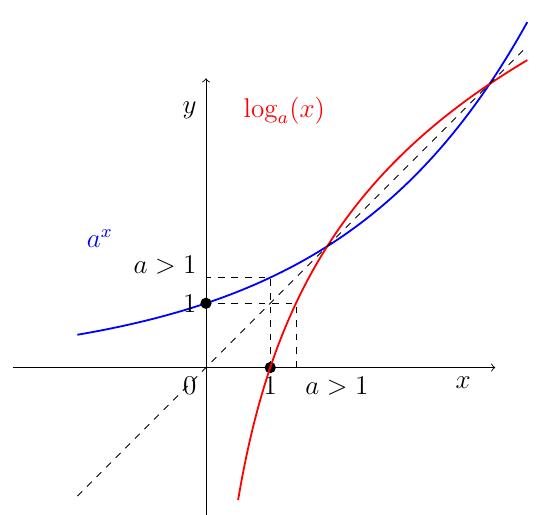
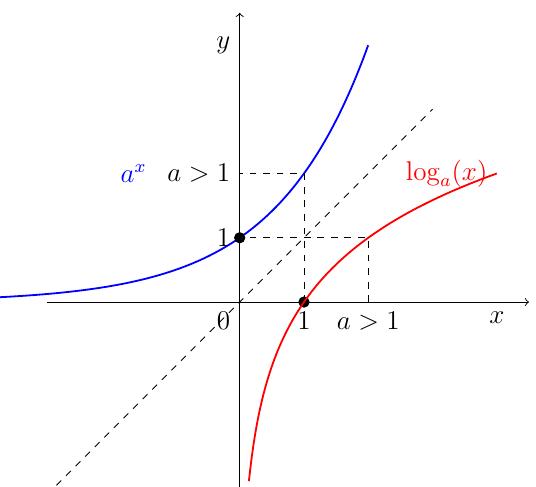
En résumé, \[ S= \begin{cases} ]2a,3a] & \text{ si } 0\lt a\lt 1\,,\\ [3a,+\infty[ & \text{ si } a\gt 1\,. \end{cases} \]

A propos des graphes de \(\log_a(x)\) et \(a^x\)

À titre de curiosité, on discute des positions relatives des graphes du logarithme et de l'exponentielle, lorsqu'on change la base \(a\). Cette discussion peut s'accompagner de l'animation du dessus, dans laquelle on peut faire varier \(a\).

  1. Cas où \(0\lt a\lt 1\): les courbes se croisent au moins une fois, sur la droite \(x=y\).
  2. Cas où \( 1\lt a \lt e^{\frac{1}{e}}\): les courbes se croisent deux fois sur la droite \(x=y\).
  3. Cas où \(a=e^{\frac{1}{e}}\): les courbes se croisent une fois sur la droite \(x=y\).
  4. Cas où \(a \gt e^{\frac{1}{e}}\) : les courbes ne se croisent pas.

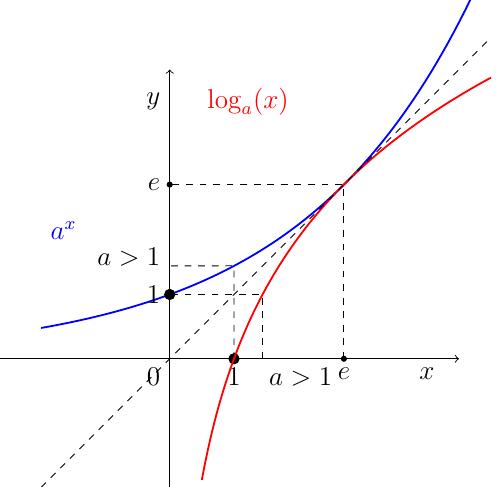
Remarque: On remarque que dans dans certains cas, il existe un nombre \(x_0\) (ou deux) tel que \[x_0=a^{x_0}=\log_a(x_0).\] On appelle ce \(x_0\) un point fixe. On peut par exemple calculer la valeur critique de la base \(a\) pour laquelle il n'y a plus de points fixes. La situation "limite" est quand les graphes de \(a^x\) et \(\log_a(x)\) se croisent en un seul point sur la droite \(x=y\) et sont tangents en ce point à la droite (qui est de pente 1). Ceci amène à résoudre (par exemple) les équations : \[x_0 = \log_a(x_0) = \frac{\ln(x_0)}{\ln(a)}, \quad \log_a^{'}(x_0)= \frac{1}{\ln(a)x_0}=1.\] En résolvant par rapport \(\ln(a)\) et \(x_0\), on trouve finalement \[x_0=e, \quad \ln(a) = \frac{1}{e} \Leftrightarrow a=e^{\frac{1}{e}}.\]

Dernière compilation: 2025-06-01 (06:48:34)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)