3.2 Les fonctions trigonométriques
Sinus, cosinus
Soient \(\alpha \in \mathbb{R}\) un angle trigonométrique, et soit \(P(\alpha)\)
son point associé, de coordonnées \((x,y)\).
- On définit le cosinus de \(\alpha\), noté \(\cos(\alpha)\), comme
l'abcisse de \(P(\alpha)\):
\[\cos(\alpha)=x.\]
- On définit le sinus de \(\alpha\), noté \(\sin(\alpha)\), comme
l'ordonnée de \(P(\alpha)\):
\[\sin(\alpha)=y.\]
L'animation ci-dessous permet d'illustrer ces fonctions, pour des angles
\(\alpha\in[0,2\pi[\):
Les propriétés suivantes sont conséquences directes
des définitions du sinus et du cosinus.
Pour tout \(\alpha \in \mathbb{R}\),
-
\(\cos(\alpha)\in [-1,1]\),
\(\sin(\alpha) \in [-1,1]\)
- \(\cos^2(\alpha) + \sin^2(\alpha)=1\)
- Si \(P(\alpha)\in I\), \(\cos(\alpha)\geqslant 0\), \(\sin(\alpha) \geqslant 0\).
- Si \(P(\alpha)\in II\), \(\cos(\alpha)\leqslant 0,\sin(\alpha) \geqslant 0\).
- Si \(P(\alpha)\in III\), \(\cos(\alpha)\leqslant 0\), \(\sin(\alpha) \leqslant 0\).
- Si \(P(\alpha)\in IV\), \(\cos(\alpha) \geqslant 0, \sin(\alpha) \leqslant 0\).
- Comme \(P(\alpha+k2\pi) = P(\alpha)\)
\(\forall k\in \mathbb{Z}\), on a que pour tout \(k \in \mathbb{Z}\),
\[\begin{aligned}
\cos(\alpha + k 2 \pi) &= \cos(\alpha)\,,\\
\sin(\alpha + k 2 \pi) &= \sin(\alpha)\,.
\end{aligned}\]
On dit que ces fonctions sont périodiques,
de période \(2\pi\).
Elles ne sont donc ni monotones, ni injectives.
De plus, les propriétés et les symétries du cercle trigonométrique impliquent
les relations suivantes:
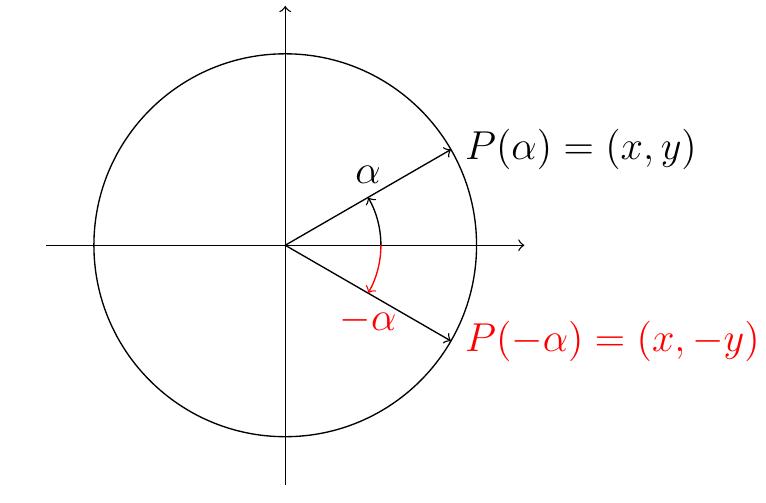
- Angles opposés (symétrie axiale d'axe \(Ox\)):
\[
\cos(-\alpha) = \cos(\alpha)
\qquad
\sin(-\alpha)=-\sin(\alpha)
\]
En d'autres termes: \(x\mapsto \cos(x)\) est une fonction paire, et \(x\mapsto
\sin(x)\) est une fonction impaire.
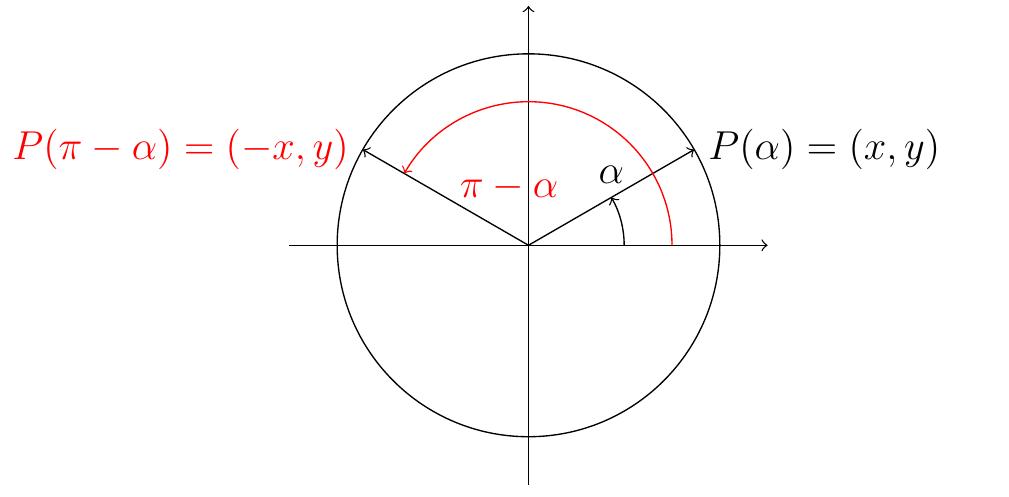
- Angles supplémentaires (symétrie axiale d'axe \(Oy\)):
\[
\cos(\pi - \alpha) = - \cos(\alpha)
\qquad
\sin(\pi-\alpha) = \sin(\alpha)
\]
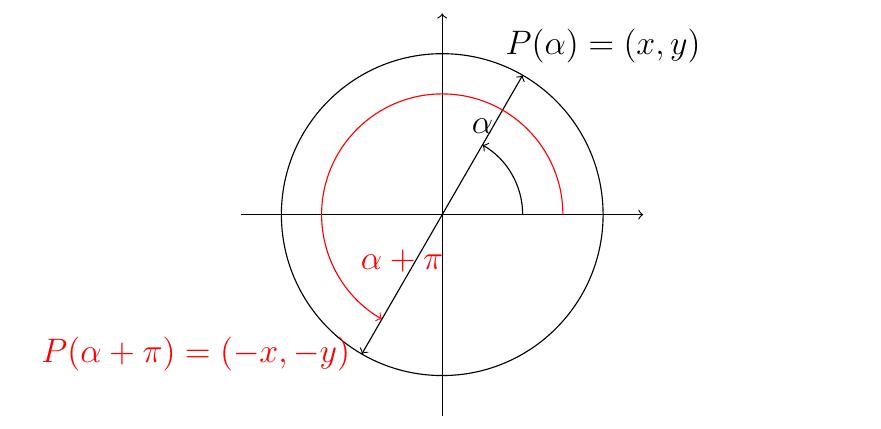
- Angles diamétralement opposés (symétrie centrale):
\[
\cos( \alpha+ \pi) = - \cos(\alpha)
\qquad
\sin(\alpha+\pi) = -\sin(\alpha)
\]
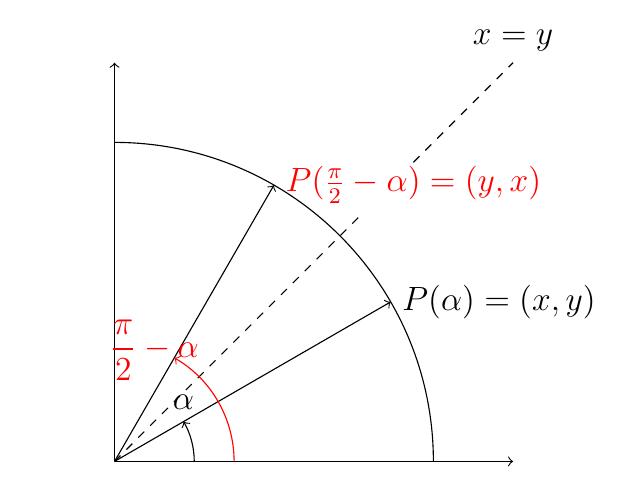
- Angles complémentaires (symétrie axiale d'axe \(x=y\)):
\[
\cos\left(\frac{\pi}{2}-\alpha\right)=\sin(\alpha)
\qquad
\sin\left(\frac{\pi}{2}-\alpha\right)=\cos(\alpha)
\]
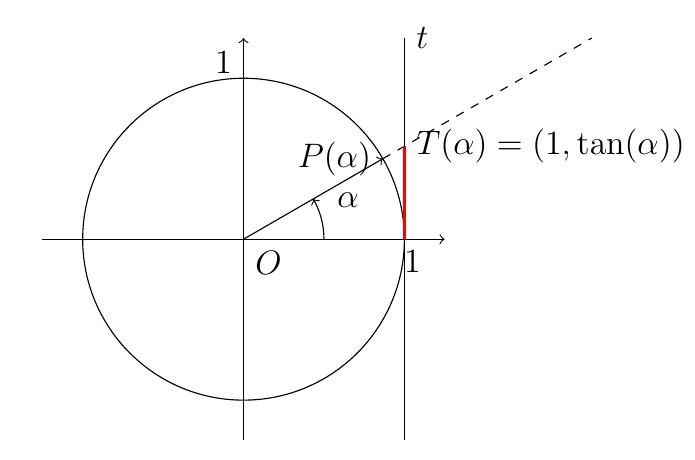
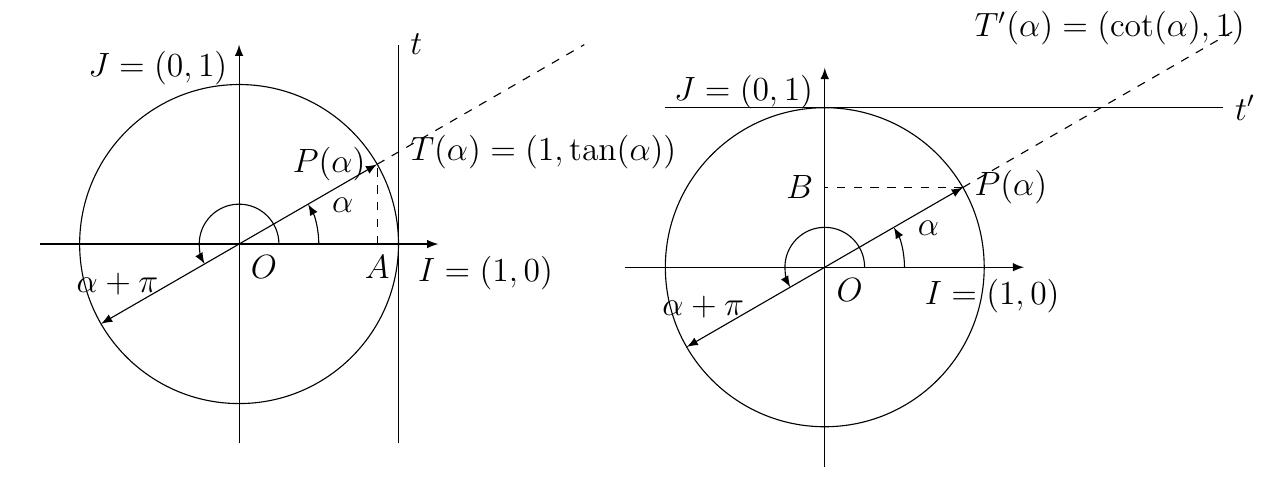
Tangente et cotangente
Soit \(t\) la droite perpendiculaire à l'axe \(Ox\) en \((1,0)\),
soit
\(\alpha\) un angle trigonométrique et \(P(\alpha)\) son point associé sur le
cercle. Soit \(T(\alpha)=(1,y)\) le point d'intersection de \(t\) avec la droite
\(OP(\alpha)\).
La tangente de l'angle \(\alpha\), notée \(\tan(\alpha)\), est définie comme
l'ordonnée du point \(T(\alpha)\).
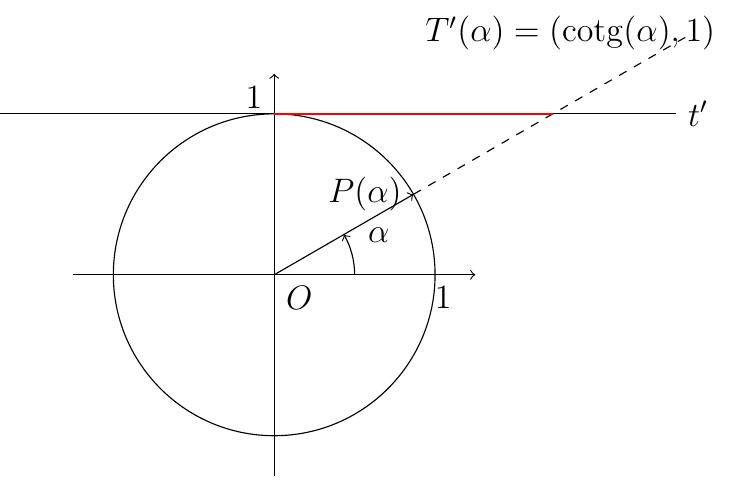
Soit \(t'\) la droite perpendulaire à l'axe \(Oy\) en \((0,1)\),
soit
\(\alpha\) un angle trigonométrique et \(P(\alpha)\) son point associé sur le
cercle. Soit \(T'(\alpha)=(x,1)\) le point d'interesection de \(t'\) avec la
droite \(OP(\alpha)\).
La cotangente de l'angle \(\alpha\), notée
\(\cot(\alpha)\), est définie comme l'abcisse du point \(T'(\alpha)\).
On a les propriétés suivantes:
- La tangente n'est pas définie pour
\(\alpha = \frac{\pi}{2} + k\pi\), \(\forall k \in \mathbb{Z}\).
Donc son domaine de définition est
\(D_{\tan}=\mathbb{R}\setminus\left\{ \frac{\pi}{2} + k\pi,k \in \mathbb{Z}\right\}\).
- La cotangente n'est pas définie pour \(\alpha=k\pi, \forall k \in \mathbb{Z}\).
Donc son domaine de définition est
\(D_{\cot}=\mathbb{R}\setminus\left\{ k\pi,k \in \mathbb{Z}\right\}\).
- Pour tout \(k \in \mathbb{Z}\),
\[\begin{aligned}
\tan(\alpha + k\pi) = \tan(\alpha)\qquad \forall \alpha\in D_{\tan}\,\\
\cot(\alpha+k\pi) = \cot(\alpha)\qquad \forall \alpha\in D_{\cot}\,.
\end{aligned}\]
Ces fonctions sont périodiques, de période \(\pi\).
- Sur \(D_{\tan}\),
\[
\tan(\alpha) = \frac{\sin(\alpha)}{\cos(\alpha)}\,.
\]
- Sur \(D_{\cot}\),
\[
\cot(\alpha) = \frac{\cos(\alpha)}{\sin(\alpha)}=\frac{1}{\tan(\alpha)}\,.
\]
-
Ces fonctions sont impaires:
\[
\tan(-\alpha)=-\tan(\alpha)\,,\qquad
\cot(-\alpha)=-\cot(\alpha)\,.
\]
On a aussi les symétries suivantes:
- \(\tan(\pi-\alpha) = -\tan(\alpha)\),
\(\cot(\pi-\alpha)=-\cot(\alpha)\).
- \(\tan\left(\frac{\pi}{2}-\alpha\right)
= \cot(\alpha)\) et
\(\cot\left(\frac{\pi}{2}-\alpha\right) = \tan(\alpha)\).
Fonctions trigonométriques pour des angles remarquables
Les fonctions trigonométriques, à l'origine, sont faites pour résoudres des
problèmes de géométrie élémentaire.
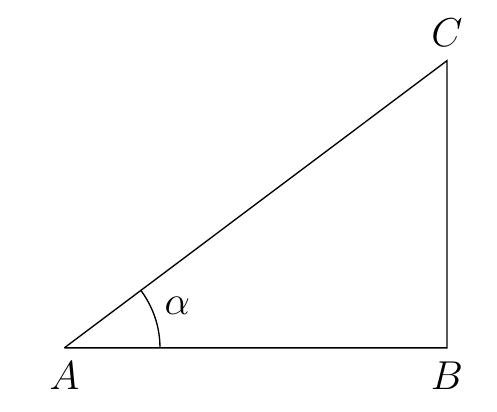
Si on considère un triangle rectangle,
on remarque que les fonctions trigonométriques représentent la proportionnalité
constante existant
entre les longueurs de certaines paires de côtés:
\[\begin{aligned}
\cos(\alpha) &= \frac{\text{côté adjacent}}{\text{hypothénuse}}=\frac{AB}{AC}\\
\sin(\alpha) &= \frac{\text{côté opposé}}{\text{hypothénuse}}=\frac{BC}{AC}\\
\tan(\alpha) &= \frac{\text{côté opposé}}{\text{côté adjacent}}=\frac{BC}{AB}\\
\end{aligned}\]
Ceci permet de calculer les valeurs des fonctions trigonométriques, pour
des angles particuliers, dits remarquables.
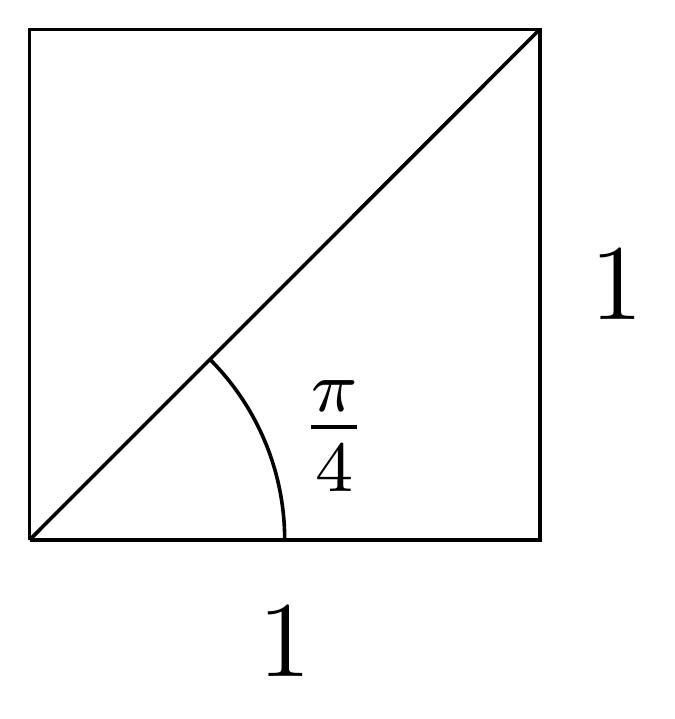
- Pour l'angle
\(\frac{\pi}{4}\), considérons un carré de côté \(1\):
Par le Théorème de Pythagore, la diagonale de ce carré
vaut \(\sqrt{2}\), et donc
\[
\cos\left(\frac{\pi}{4}\right)
=\sin\left(\frac{\pi}{4}\right)
=\frac{1}{\sqrt{2}}
=\frac{\sqrt{2}}{2}
\]
(Dans la dernière égalité, on a multiplié la fraction par
\(1=\frac{\sqrt{2}}{\sqrt{2}}\).)
Aussi,
\[
\tan\left(\frac{\pi}{4}\right)=1\,.
\]
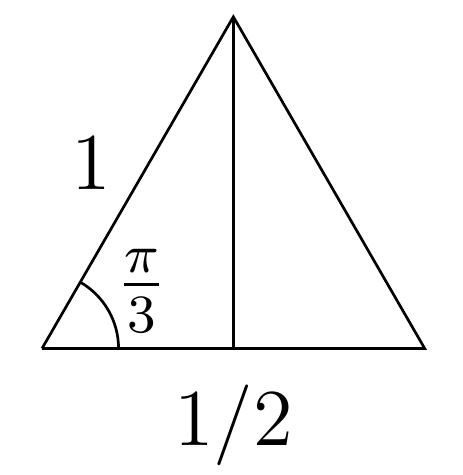
- Pour l'angle \(\frac{\pi}{3}\), considérons
un triangle équilatéral de côté \(1\):
La hauteur de ce triangle est de longueur
\(\frac{\sqrt{3}}{2}\), et elle intersecte le côté horizontal en son milieu.
On a donc
\[
\cos\left(\frac{\pi}{3}\right)
=\frac{1}{2},\qquad
\sin\left(\frac{\pi}{3}\right)
=\frac{\sqrt{3}}{2}\,,
\qquad
\tan\left(\frac{\pi}{3}\right)=
\frac{\sqrt{3}/2}{1/2}=
\sqrt{3}\,.
\]
On peut obtenir les valeurs des fonctions trigonométriques pour l'angle
\(\frac{\pi}{6}\) de la même façon.
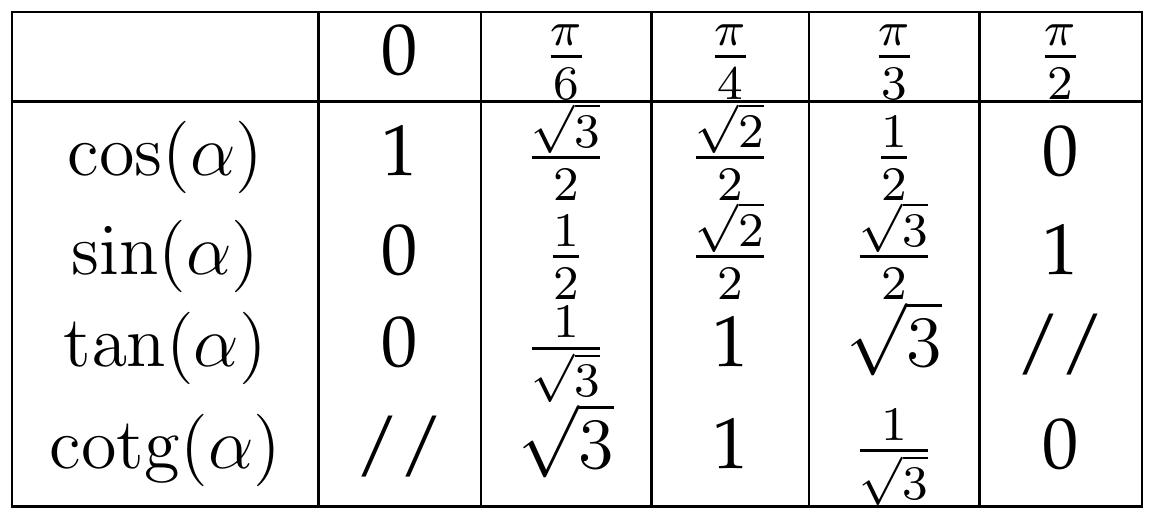
Résumons ce qu'on a obtenu jusqu'à présent dans le tableau suivant.
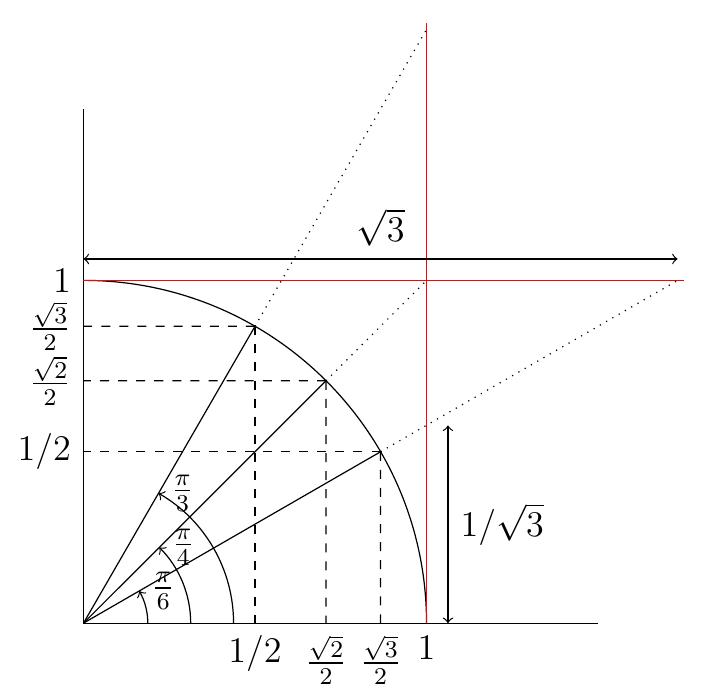
Représentation et construction géométrique des angles remarquables dans le
premier quadrant: