3.3 Les 4 équations élémentaires
On va présenter la résolution de chacune des quatre
équations trigonométriques élémentaires, qui sont:
\[
\cos(x)=a, \quad
\sin(x)=a, \quad
\tan(x)=a, \quad
\cot(x)=a.
\]
- A l'avenir quand nous traiterons des équations plus complexes, la
stratégie sera toujours de se ramener à l'une de ces équations élémentaires.
- La résolution est basée sur la nature du cercle trigonométrique qui
implique que des angles différents peuvent avoir des cosinus et sinus
identiques. (Par exemple, deux angles supplémentaires ont le même sinus, deux
angles opposés ont le même cosinus.)
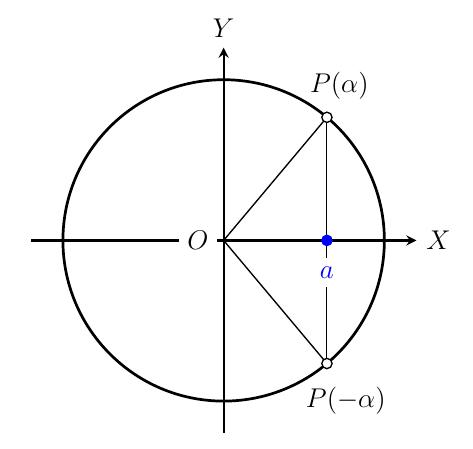
L'équation \(\cos(x)=a\)
- L'équation possède des solutions si \(a\in[-1,1]\).
- L'équation est bien définie pour tout \(x\in\mathbb{R}\).
- On cherche un angle \(\alpha\) tel que \(\cos(\alpha)=a\) (par exemple parmi les valeurs remarquables).
- On doit donc résoudre \(\cos(x)=\cos(\alpha)\). Deux cosinus sont égaux si les angles sont les mêmes ou sont opposés, le tout à \(2\pi\) près.
- Solution :
\[\cos(x)=\cos(\alpha) \quad\Leftrightarrow\quad
x=\alpha + k2\pi \quad\text{ ou }\quad x=-\alpha + k2\pi, \quad k\in \mathbb{Z}.\]
Exemple:
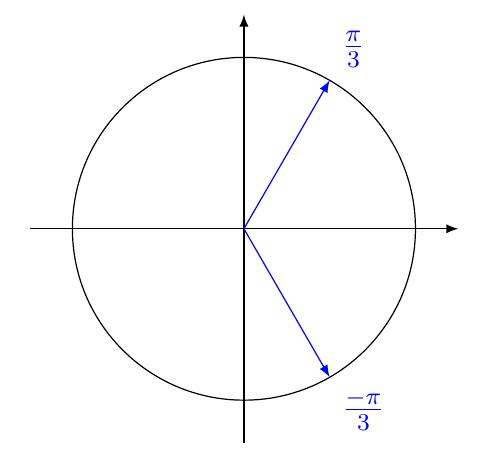
Résoudre pour \(x\in\mathbb{R}\): \(\cos(x)=\frac{1}{2}\).
On sait que \(\cos\left(\frac{\pi}{3}\right)=\frac{1}{2}.\)
On résout donc
\(\cos(x)=\cos\left(\frac{\pi}{3}\right)\)
et on a deux familles de solutions:
\[
x=\frac{\pi}{3} + k2\pi \quad \text{ ou }\quad
x=-\frac{\pi}{3} + k2\pi, \quad k\in \mathbb{Z}\,.
\]
Et donc
\[
S=\left\{ \pm \frac{\pi}{3} + k2\pi, k\in \mathbb{Z}\right\}\,.
\]
Exemple:
Résoudre pour \(x\in\mathbb{R}\) : \(\cos(2x)=\frac{1}{2}\).
On pose \(y=2x\) et on commence par résoudre
\(\cos(y)=\frac{1}{2}\).
On trouve deux familles de solutions
\[
y_1= \frac{\pi}{3} + k2\pi
\quad\text{ ou }\quad
y_2=- \frac{\pi}{3} + k2\pi, \quad k\in \mathbb{Z}\,.
\]
Chaque famille génère un point associé sur le cercle.
En repassant dans la variable \(x\), on trouve donc
\[
2x= \frac{\pi}{3} + k2\pi
\quad\text{ ou }\quad
2x=- \frac{\pi}{3} + k2\pi,\quad
k\in \mathbb{Z}\]
et donc
\[x_1=\frac{\pi}{6} + k\pi \quad\text{ ou }\quad
x_2=-\frac{\pi}{6} + k\pi, \quad k\in \mathbb{Z}.\]
Afin de visualiser, représentons certaines solutions sur le cercle.
On peut par exemple prendre les solutions \(x_1\) et \(x_2\), pour \(k=0,1,2\).
On voit que les deux familles de solutions génèrent ici 4 points associés, et
non plus seulement deux. Chaque famille génère en fait un couple de points
diamétralement opposés (à cause du \(k\pi\), qui représente
des demi-tours supplémentaires).
Exemple:
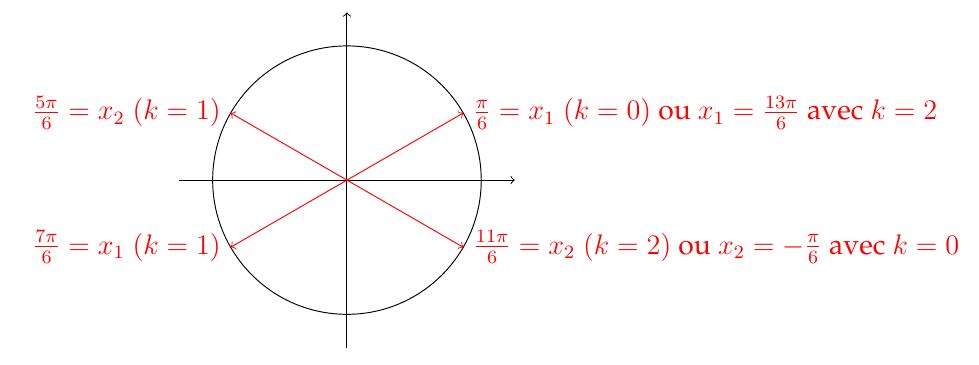
Résoudre pour \(x\in\left[0,2\pi\right]\) : \(\cos(2x)=\frac{1}{2}\).
L'équation est la même qu'avant, mais la contrainte ''\(x\in\left[0,2\pi\right]\)''
impose de garder seulement les solutions appartenant à cet intervalle.
- On résout tout d'abord le problème pour \(x\in\mathbb{R}\). Par ce qui précède,
on a trouvé que
\[
x_1=\frac{\pi}{6} + k\pi,
\quad\text{ ou }\quad
x_2=-\frac{\pi}{6} + k\pi, \quad k\in \mathbb{Z}\,.\]
- On résout maintenant sur l'intervalle \(\displaystyle
\left[0,2\pi\right]\). Il faut chercher \(k\) pour que \(x_1\) et \(x_2\)
appartiennent à cet intervalle.
On procède en s'aidant de la représentation : on se place en zéro et
on tourne dans le sens trigonométrique jusqu'à atteindre \(2\pi\) et on capture
au passage tous les angles qui nous intéressent.
On peut donc choisir \(x_1\) avec \(k=0,1\) et \(x_2\) avec \(k=1,2\). Pour les
autres \(k\), on sort de l'intervalle \([0,2\pi]\).
On conclut donc que
\(S=\left\{\frac{\pi}{6},\frac{5\pi}{6},\frac{7\pi}{6},\frac{11\pi}{6}\right\}.\)
Exemple:
Résoudre pour \(x\in\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) :
\(\cos(2x)=\frac{1}{2}\).
Comme avant on résout tout d'abord le problème pour \(x\in\mathbb{R}\) et on trouve
\[
x_1=\frac{\pi}{6} + k\pi,
\quad\text{ ou }\quad
x_2=-\frac{\pi}{6} + k\pi, \quad k\in \mathbb{Z}\,.
\]
Cette fois, on ne garde que les angles compris dans l'intervalle \(\displaystyle
\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\). On procède par visualisation
- La solution \(x=\frac{\pi}{6}\) et la solution \(x=-\frac{\pi}{6}\) sont
dans le bon intervalle (\(k=0\))
- L'intervalle \(\left[-\frac{\pi}{2},\frac{\pi}{2}\right]\) est l'union des
quadrants \(IV\) et \(I\). Des angles dont les points associés seront dans
\(II\cup III\) seront à exclure.
- L'ensemble des angles solutions de l'équation donnent 4 points associés
sur le cercle. Tous les angles qui génèrent les deux points associés dans le
demi-cercle de gauche sont à exclure. Par conséquent, on doit juste s'intéresser
aux solutions dans le demi-cercle de droite. Comme on a déjà les deux solutions
\(x=\frac{\pi}{6}\) et \(x=-\frac{\pi}{6}\) qui sont dans le bon intervalle,
tous les autres angles qui envoient sur ces mêmes points seront soit strictement
plus petit que \(\frac{-\pi}{2}\) soit strictement plus grand que
\(\frac{\pi}{2}\).
On conclut donc que \(S=\left\{\frac{\pi}{6},-\frac{\pi}{6}\right\}.\)
Exemple:
Résoudre pour \(x\in\left[-4\pi,-3\pi\right]\) : \(\cos(2x)=\frac{1}{2}\).
Même exemple que le précédent mais cette fois on cherche les \(x\) dans un autre
intervalle. On voit que cette fois on doit prendre des points dans le quadrant
\(I\) ou \(II\). Pour s'aider, on représente les points sur un tour de cercle
entre \(-2\pi\) et \(0\). On rappelle les solutions
\[x_1=\frac{\pi}{6} + k\pi,\text{ ou } x_2=-\frac{\pi}{6} + k\pi, k\in \mathbb{Z}.\]
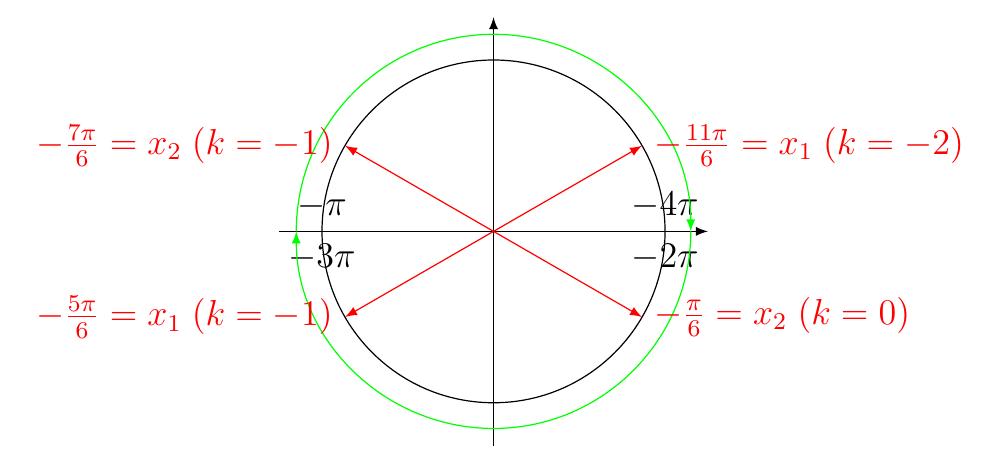
Il faut choisir le bon nombre de demi-tours/tours à faire pour être dans le bon
intervalle. Ici on peut prendre \(x_1\) avec \(k=-4\) et \(x_2\) avec \(k=-3\).
En effet, \(\frac{\pi}{6} \in [0,\pi]\) et donc en faisant 2 tours dans le sens
anti-trigonométrique (i.e \(-4\pi\)) on arrive dans l'intervalle
\([-4\pi,-3\pi]\). De même, \(\frac{-\pi}{6}\in[-\pi,0]\). En faisant trois
demi-tours dans le sens horaire (i.e \(-3\pi\)), on arrive dans le bon
intervalle. Comme on a trouvé deux angles dans \([-4\pi,-3\pi]\) qui génèrent
les deux points du demi-supérieur, on les a tous trouvé.
On prend alors comme solution \(\frac{\pi}{6} -4\pi = -\frac{23\pi}{6}\) et
\(\frac{-\pi}{6}-3\pi=-\frac{19\pi}{6}\), et donc
\(S=\left\{-\frac{19\pi}{6},-\frac{23\pi}{6}\right\}\).
L'équation \(\sin(x)=a\)
- L'équation possède des solutions si \(a\in[-1,1]\).
- L'équation est bien définie pour tout \(x\in\mathbb{R}\).
- On cherche un angle \(\alpha\) tel que \(\sin(\alpha)=a\) (par exemple parmi les valeurs remarquables).
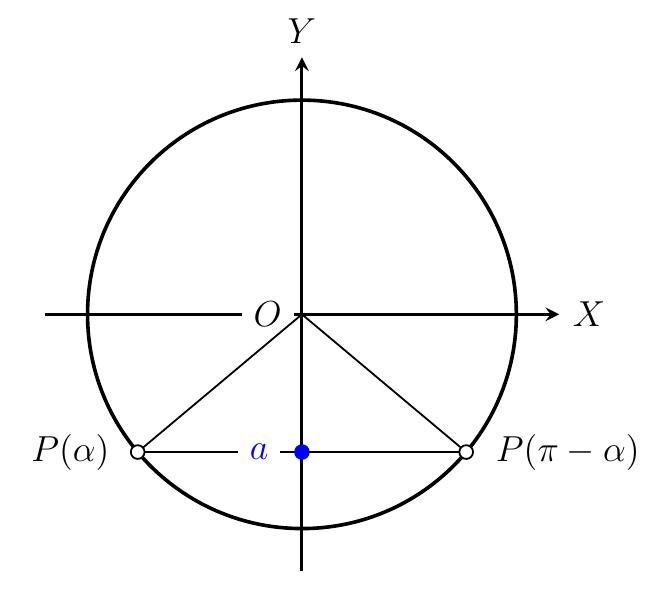
- On doit donc résoudre \(\sin(x)=\sin(\alpha)\). Deux sinus sont égaux si les angles sont les mêmes ou sont supplémentaires, le tout à \(2\pi\) près.
- Solution :
\[\sin(x)=\sin(\alpha) \quad\Leftrightarrow\quad
x=\alpha + k2\pi \quad\text{ ou }\quad x=\pi-\alpha + k2\pi, \quad k\in \mathbb{Z}.\]
Exemple:
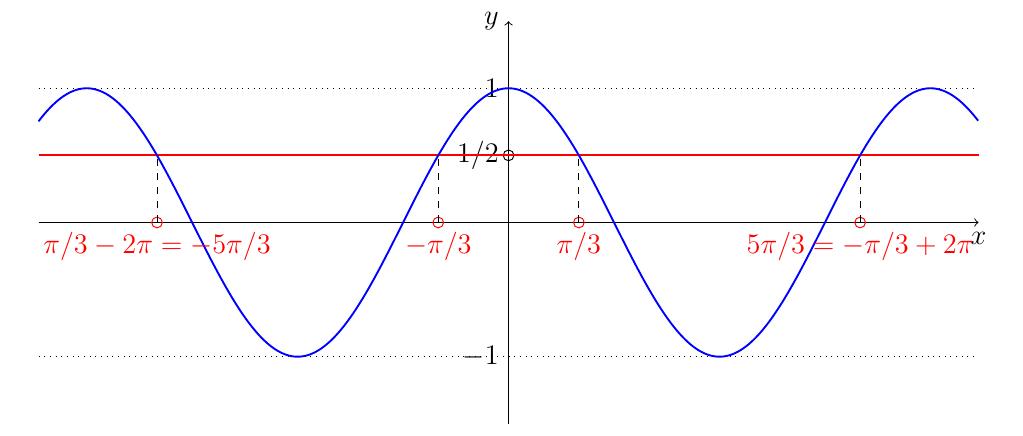
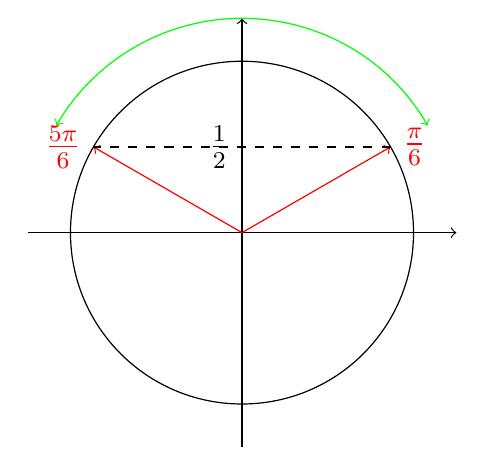
Résoudre pour \(x\in\mathbb{R}\) : \(\sin(x) \geqslant \frac{1}{2}\).
On cherche \(\alpha\) tel \(\sin(\alpha)=\frac{1}{2}\). On peut choisir par
exemple \(\alpha=\frac{\pi}{6}\). On doit donc résoudre
\[\sin(x) \geqslant \sin\left(\frac{\pi}{6}\right).\]
L'erreur serait de dire que \(x\geqslant \frac{\pi}{6}\) mais attention, les
fonctions trigonométriques ne sont pas monotones. Il est utile de considérer ce
qui se passe sur le cercle trigonométrique.
On représente dans le cercle des angles
supplémentaires pour lequel le sinus vaut \(\frac{1}{2}\).
Les points situés sur la partie verte du cercle ont des ordonnées plus grandes
que \(\frac{1}{2}\), donc les angles associés ont leur sinus plus grand que
\(\frac{1}{2}\). On doit donc choisir
\[ \frac{\pi}{6} + k2\pi \leqslant x \leqslant \frac{5\pi}{6} + k2\pi, k \in \mathbb{Z}.\]
On a donc
\(\displaystyle S=\bigcup_{k\in\mathbb{Z}} \left[\frac{\pi}{6} +k2
\pi,\frac{5\pi}{6}+k2\pi\right].\)
L'équation \(\tan(x)=a\)
- L'équation possède des solutions \(\forall a \in \mathbb{R}\).
- Le domain de définition est \(\displaystyle D_{\text{tan}}=\mathbb{R} \setminus\left\{ \frac{\pi}{2}+k\pi,k\in\mathbb{Z}\right\}.\)
- On cherche un angle \(\alpha\) tel que \(\tan(\alpha)=a\) (par exemple parmi les valeurs remarquables).
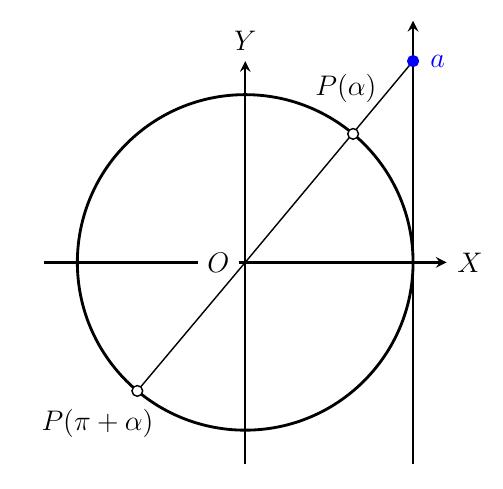
- On doit donc résoudre \(\tan(x)=\tan(\alpha)\). Deux tangentes sont égales si les angles sont les mêmes ou diffèrent d'un demi-tour.
- Solution :
\[\tan(x)=\tan(\alpha) \quad\Leftrightarrow\quad
x=\alpha + k\pi, \quad k\in \mathbb{Z}.\]
Exemple:
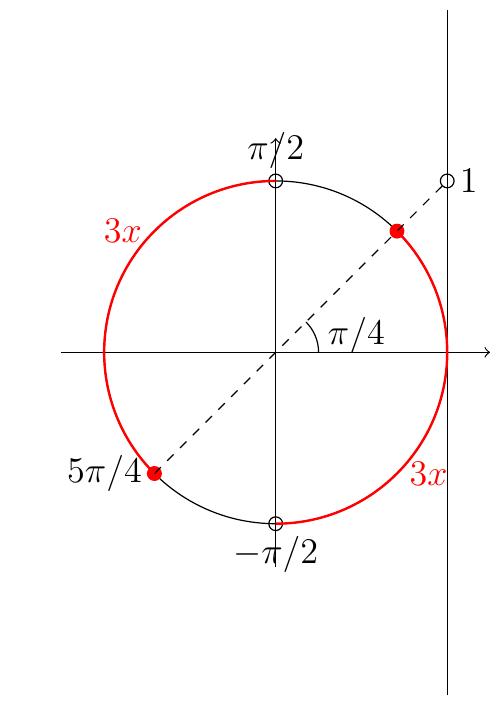
- Résoudre pour \(x\in \mathbb{R}\) : \(\tan(3x)\leqslant 1\). Considérons encore une
fois le cercle trigonométrique.
On pose d'abord \(y=3x\) et on résout
\(\tan(y)\leqslant 1\).
Les angles associés aux points situés sur les portions rouges auront des tangentes inférieures à 1. On a donc
\[ -\frac{\pi}{2} + k\pi < y \leqslant \frac{\pi}{4} + k\pi.\] Notez que le \(+k\pi\) permet de considérer les deux zones rouges d'un coup (l'une étant la rotation d'un demi-tour de l'autre) ainsi que tous les demi-tours supplémentaires. Notez aussi l'inégalité stricte à gauche car \(\frac{-\pi}{2}+k\pi\) n'est pas dans le domaine de définition de la tangente.
On a donc finalement
\[ -\frac{\pi}{6} + k\frac{\pi}{3} < x \leqslant\frac{\pi}{12} + k\frac{\pi}{3}\]
et
\[S=\bigcup_{k\in\mathbb{Z}}
\left]
-\frac{\pi}{6}+k\frac{\pi}{3},\frac{\pi}{12}+k\frac{\pi}{3}
\right]\,.
\]
Représentons certains de ces angles (par exemple pour \(k=0,1,2,3,4,5)\)):
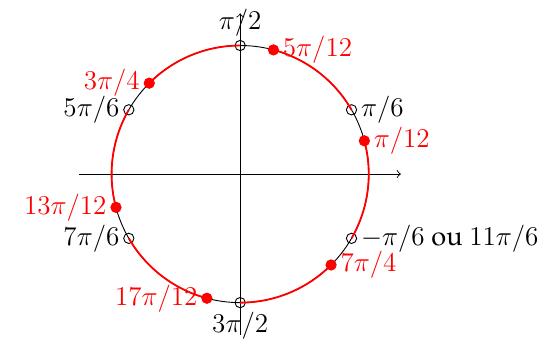
- Résoudre pour \(x\in[0,2\pi]\) : \(\tan(3x)\leqslant 1\).
On prend les solutions obtenues précédemment, et on "filtre" les intervalles pour qu'ils appartiennent tous à \([0,2\pi]\). On réfléchit géométriquement. On se place en \(0\) dans le cercle trigonométrique et on tourne jusqu'à \(2\pi\). On a donc
\[S =\left[0,\frac{\pi}{12}\right] \cup \left]\frac{\pi}{6},\frac{5\pi}{12}\right]\cup \left]\frac{\pi}{2},\frac{3\pi}{4}\right]\cup \left]\frac{5\pi}{6},\frac{13\pi}{12}\right]\cup \left]\frac{7\pi}{6},\frac{17\pi}{12}\right]\cup \left]\frac{3\pi}{2},\frac{7\pi}{4}\right]\cup \left]\frac{11\pi}{6},2\pi\right].\]
On doit faire attention au fait que l'intervalle \(\displaystyle \left]\frac{-\pi}{6},\frac{\pi}{12}\right]\) n'est pas entièrement contenu dans \([0,2\pi]\). Il faut donc "exploser" l'intervalle en prenant chaque partie dans le bon tour du cercle trigonométrique.
L'équation \(\cot(x)=a\)
- L'équation possède des solutions \(\forall a \in \mathbb{R}\).
- Le domain de définition est \(\displaystyle D_{\text{cot}}=\mathbb{R} \setminus\left\{ k\pi,k\in\mathbb{Z}\right\}.\)
- On cherche un angle \(\alpha\) tel que \(\cot(\alpha)=a\) (par exemple parmi les valeurs remarquables).
- On doit donc résoudre \(\cot(x)=\cot(\alpha)\). Deux cotangentes sont égales si les angles sont les mêmes ou diffèrent d'un demi-tour.
- Solution :
\[\cot(x)=\cot(\alpha)
\quad\Leftrightarrow\quad
x=\alpha+k\pi, \quad k\in \mathbb{Z}.\]