3.4 Formules trigonométriques

Préparation: une rotation dans le plan

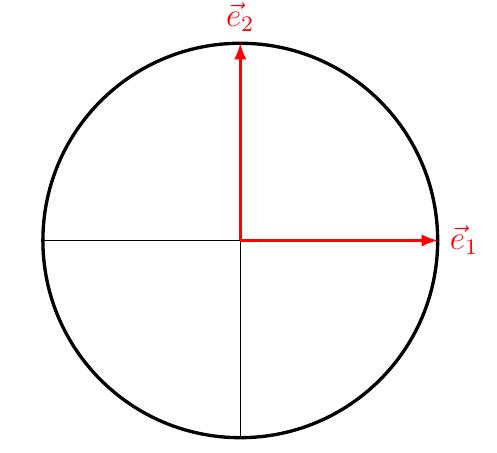
Considérons le cercle trigonométrique dans le repère orthonormé canonique \((\vec{e}_1,\vec{e}_2)\):

Si on fait tourner le repère d'un angle \(\beta\), on obtient deux nouveaux vecteurs \(\vec{f}_1\) et \(\vec{f}_2\):

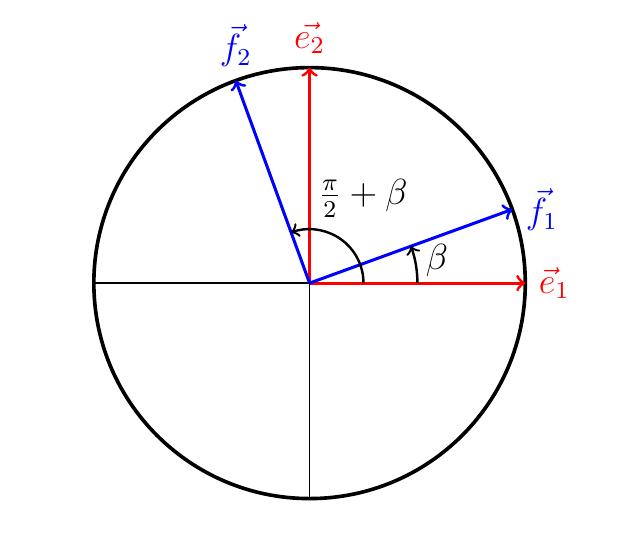
Ces derniers s'écrivent \[ \vec{f}_1 = \cos(\beta) \vec{e}_1 + \sin(\beta)\vec{e}_2\,, \] et \[ \vec{f}_2 = \cos(\tfrac{\pi}{2}+\beta) \vec{e}_1 + \sin(\tfrac{\pi}{2}+\beta)\vec{e}_2 =-\sin(\beta) \vec{e}_1 + \cos(\beta)\vec{e}_2\,. \] Prenons maintenant un angle \(\alpha\in \mathbb{R}\), et son point associé \(P(\alpha)\) sur le cercle. Relativement au repère \((\vec{e}_1,\vec{e}_2)\), \[ \overrightarrow{OP(\alpha)}= \cos(\alpha)\vec{e}_1 + \sin(\alpha)\vec{e}_2\,. \] Après une rotation d'angle \(\beta\), \(P(\alpha)\) devient \(P(\alpha+\beta)\):

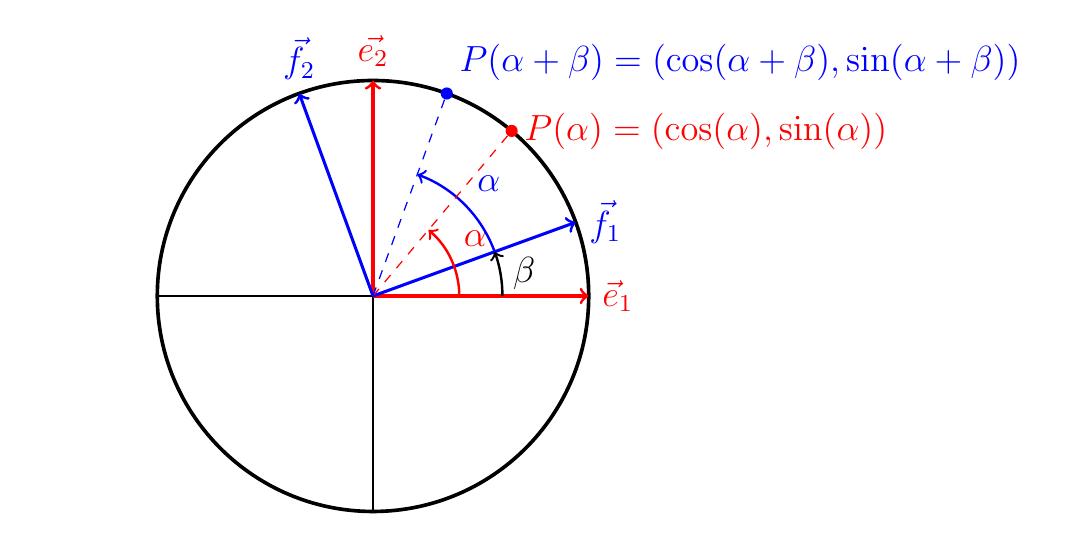
Relativement à \((\vec{e}_1,\vec{e}_2)\), \[ \overrightarrow{OP(\alpha + \beta)}=\cos(\alpha+\beta) \vec{e}_1 + \sin(\alpha+\beta)\vec{e}_2\,. \] Mais, relativement à \((\vec{f}_1,\vec{f}_2)\), \[ \overrightarrow{OP(\alpha + \beta)}=\cos(\alpha) \vec{f}_1 + \sin(\alpha)\vec{f}_2\,, \] et en utilisant les relations données plus haut, exprimant les vecteurs de \((\vec{f}_1,\vec{f}_2)\) en fonction de ceux de \((\vec{e}_1,\vec{e}_2)\), et en réarrangeant, cette dernière devient \[\begin{aligned} &\overrightarrow{OP(\alpha + \beta)}\\ &= \cos(\alpha) \bigl(\cos(\beta) \vec{e}_1 + \sin(\beta)\vec{e}_2\bigr) +\sin(\alpha) \bigl(-\sin(\beta) \vec{e}_1 + \cos(\beta)\vec{e}_2\bigr)\\ &=\bigl(\cos(\alpha) \cos(\beta) - \sin(\alpha)\sin(\beta)\bigr)\vec{e}_1 + \bigl(\sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta)\bigr)\vec{e}_2. \end{aligned}\] Comme les composantes de \(\overrightarrow{OP(\alpha + \beta)}\) relativement au repère \((\vec{e}_1,\vec{e}_2)\) sont uniques, on en déduit que \[\begin{aligned} \cos(\alpha + \beta) &=\cos(\alpha) \cos(\beta) - \sin(\alpha)\sin(\beta) \\ \sin (\alpha + \beta) &=\sin(\alpha)\cos(\beta) + \cos(\alpha)\sin(\beta) \end{aligned}\]

Conséquence: formules d'addition

L'argument algébrique/géométrique de la section précédente nous a amené aux formules d'addition: \[\begin{aligned} \cos(x+y)&=\cos(x)\cos(y)-\sin(x)\sin(y)\\ \sin(x+y)&=\sin(x)\cos(y)+\cos(x)\sin(y)\,. \end{aligned}\] Celles-ci impliquent aussi une formule d'addition pour la tangente, puisque \[\begin{aligned} \tan (x + y) &=\frac{\sin(x+y)}{\cos(x+y)}\\ &= \frac{\sin(x)\cos(y)+\cos(x)\sin(y)}{\cos(x)\cos(y)-\sin(x)\sin (y)}\\ &= \frac{\tan(x)+\tan(y)}{1-\tan(x)\tan(y)}\,. \end{aligned}\] (Dans la troisième ligne on a divisé numérateur et dénominateur par \(\cos(x)\cos(y)\).)

En remplaçant \(y\) par \(-y\) dans les formules d'addition et en utilisant les propriétés de parité, on obtient aussi \[\begin{aligned} \sin(x-y)&=\sin(x)\cos(y)-\cos(x)\sin(y)\\ \cos(x-y)&=\cos(x)\cos(y)+\sin(x)\sin(y)\\ \tan(x-y)&=\frac{\tan(x)-\tan(y)}{1+\tan(x)\tan(y)} \end{aligned}\] D'autres expressions utiles se déduisent des formules d'addition.

• Formules pour le double d'un angle ou Formules de duplication. En prenant \(x=y\) dans les formules d'addition, on a d'une part que \[ \sin(2x)=2\sin(x)\cos(x)\,, \] et d'autre part que \[ \cos(2x)=\cos^2(x)-\sin^2(x) =1-2\sin^2(x) =2\cos^2(x)-1 \]
• Formules de bissection. En remplaçant \(x\) par \(x/2\) dans les formules du double d'un angle: \[\begin{aligned} \sin^2(\tfrac{x}{2})&=\frac{1-\cos(x)}{2}\\ \cos^2(\tfrac{x}{2})&=\frac{1+\cos(x)}{2}\\ \tan^2(\tfrac{x}{2})&=\frac{1-\cos(x)}{1+\cos(x)} \end{aligned}\]
• Formules de transformation produit-somme. \[\begin{aligned} \cos (x) \cdot \cos (y) &= \tfrac{1}{2}[\,\cos (x+y) + \cos (x-y)\,]\\ \sin (x) \cdot \sin (y) &= -\tfrac{1}{2} [\,\cos (x+y) - \cos (x-y)\,]\\ \sin (x) \cdot \cos (y) &= \tfrac{1}{2} [\,\sin (x+y) + \sin (x-y)\,] \end{aligned}\] (On démontre ces formules en partant du terme de droite, auquel on applique les formules du haut.)
• Formules de transformation somme-produit. En remplaçant \(x\) par \(\frac{x+y}{2}\) et \(y\) par \(\frac{x-y}{2}\) dans les formules de produit-somme, \[\begin{aligned} \cos(x)+\cos(y) &=2\cos(\tfrac{x+y}{2})\cos(\tfrac{x-y}{2})\\ \cos(x)-\cos(y) &=-2\sin(\tfrac{x+y }{2})\sin(\tfrac{x-y}{2}) \end{aligned}\] et \[\begin{aligned} \sin(x)+\sin(y) &=2\sin(\tfrac{x+y}{2})\cos(\tfrac{x-y}{2})\\ \sin(x)-\sin(y) &=2\cos(\tfrac{x+y }{2})\sin(\tfrac{x-y}{2}) \end{aligned}\]
• Expressions des fonctions trigonométriques en fonction de \(\tan (\frac{x}{2})\). À partir des formules de bissections et de double d'un arc, \[\begin{aligned} \sin x &= \frac{2 \tan (\frac{x}{2})}{1 + \tan^2 (\frac{x}{2})}\\ \cos x &= \frac{1 - \tan^2 (\frac{x}{2})}{1 + \tan^2 (\frac{x}{2})} \\ \tan x &= \frac{2 \tan (\frac{x}{2})}{1 - \tan^2 (\frac{x}{2})} \end{aligned}\]

Application : dérivées des fonctions trigonométriques

A l'aide des formules de transformation somme-produit, on peut obtenir les expressions des dérivées des fonctions trigonométriques: \[\begin{aligned} (\sin(x))' &= \cos(x), \\ (\cos(x))' &= -\sin(x), \\ (\tan(x))' &= 1 + \tan^2(x) = \frac{1}{\cos^2(x)}\,. \end{aligned}\] En effet, \[\begin{aligned} (\sin(x))' &= \lim_{y\rightarrow x}\frac{\sin(y)-\sin(x)}{y-x} \\ &= \lim_{y\rightarrow x} \frac{2\cos\left(\frac{y+x}{2}\right)\sin \left(\frac{y-x}{2}\right)}{y-x} \\ &= \left( \lim_{y\rightarrow x} \cos\bigl(\tfrac{y+x}{2}\bigr) \right) \left( \lim_{y\rightarrow x} \frac{\sin\left(\frac{y-x}{2}\right)}{\frac{y-x}{2}} \right) =\cos(x) \cdot 1=\cos(x)\,. \end{aligned}\] On en déduit, par la formule de la dérivation d'une composée, que \[ (\cos(x))' =\bigl(\sin(\tfrac{\pi}{2}-x)\bigr)' =\cos(\tfrac{\pi}{2}-x)\cdot (-1) =-\sin(x)\,, \] et par la formule de dérivation d'un quotient, \[\begin{aligned} (\tan(x))' &= \left(\frac{\sin(x)}{\cos(x)}\right)'\\ &= \frac{\cos(x)\cos(x)-\sin(x)(-\sin(x))}{\cos^2(x)}\\ &= \frac{1}{\cos^2(x)}=1+\tan^2(x)\,. \end{aligned}\] De même on peut calculer que \[ (\cot(x))' =\frac{-1}{\sin^2(x)} =-1-\cot^2(x)\,. \]

Application : calcul de valeurs remarquables supplémentaires

De manière générale, on peut calculer à présent les cosinus et sinus de tout angle de la forme \(\frac{\alpha}{2^n}, n\in \mathbb{N}\) pour \(\alpha\) une valeur remarquable dans le premier quadrant. On pourra obtenir les cosinus et sinus de ces angles dans les autres quadrants en utilisant les propriétés des cosinus et sinus (symétriques par rapport aux axes et par rapport à l'origine).

Application : factorisation en équations/inéquations plus simples

Equations et inéquations trigonométriques linéaires

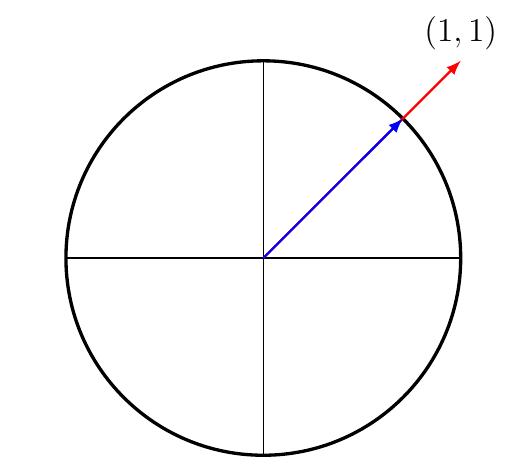
Exemple: Résolvons l'inéquation \[\cos(x) + \sin(x) \gt 1,\qquad x\in]-4\pi,-\pi[\,. \] On commence par résoudre le problème sans contrainte (pour \(x\in \mathbb{R}\)). La stratégie est la même que précédemment. Idéalement, on aimerait un angle \(\alpha\) tel que \(\sin(\alpha)=\cos(\alpha)=1\) afin d'écrire le membre de droite comme une seule fonction trigonométrique. On observe cependant qu'un tel angle n'existe pas car le point \((1,1)\) n'appartient pas au cercle trigonométrique.

En considérant le vecteur reliant l'origine à \((1,1)\) et en divisant par sa norme qui vaut \(\sqrt{2}\), on obtient un nouveau vecteur de norme 1 dont l'extrémité est le point \((1/\sqrt{2},1/\sqrt{2})=(\sqrt{2}/2,\sqrt{2}/2)\) se trouve sur le cercle trigonométrique et dont les coordonnées peuvent être exprimées comme le cosinus et le sinus d'un angle. On a donc fait une normalisation.

En divisant chaque côté de l'inéquation par \(\sqrt{2}\), elle devient \[ \tfrac{\sqrt{2}}{2}\cos(x)+\tfrac{\sqrt{2}}{2}\sin(x) \gt \tfrac{\sqrt{2}}{2} \] qui puisque \(\frac{\sqrt{2}}{2}=\sin(\frac{\pi}{4})=\cos(\frac{\pi}{4})\) se simplifie encore en \[ \sin\left(\tfrac{\pi}{4}+x\right) \gt \sin(\pi/4)\,. \] On visualise dans le cercle trigonométrique,

pour trouver \[ \tfrac{\pi}{4} + k2\pi \lt \tfrac{\pi}{4}+x \lt \tfrac{3\pi}{4} + k2\pi, \qquad k\in\mathbb{Z}\] et donc l'ensemble solution sans contrainte est \[E = \bigcup_{k\in\mathbb{Z}} \left] k2\pi,\tfrac{\pi}{2} + k2\pi\right[\,.\] Finalement, on ne garde que les \(x\in E\) qui satisfont la contrainte \(x\in ]-4\pi,-\pi[\), pour obtenir \[S = \left]-4\pi,-\tfrac{7\pi}{2}\right[ \cup \left]-2\pi,-\tfrac{3\pi}{2}\right[.\]

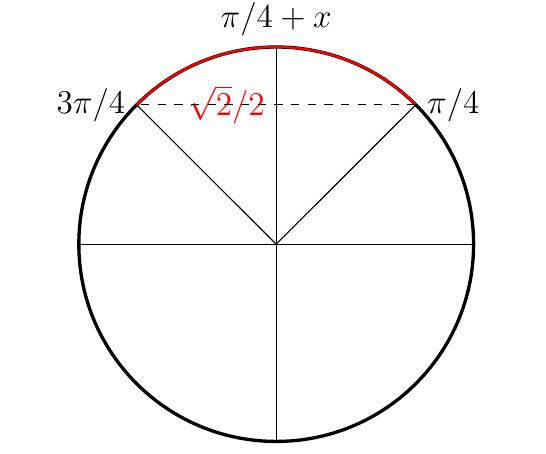
Dans un cadre plus général, la méthode utilisée dans l'exemple précédent suggère que pour résoudre une équation de la forme \[a \cos(x) + b\sin(x) = c\,,\] où \(a,b,c\in\mathbb{R}\), on pourra procéder comme suit:

1. On normalise l'équation en divisant par \(\sqrt{a^2 + b^2}\) (la norme de \(\overrightarrow{OP}\), avec \(P=(a,b)\)): \[ \frac{a}{\sqrt{a^2 + b^2}}\cos(x) + \frac{b}{\sqrt{a^2+b^2}}\sin(x) = \frac{c}{\sqrt{a^2+b^2}}\,. \]
2. Si \(\frac{c}{\sqrt{a^2+b^2}}\in[-1,1]\), on peut résoudre le problème (il faut que ce nombre soit le sinus ou le cosinus d'un angle, un critère simple est de vérifier si \(a^2 + b^2 \leqslant c^2 \Leftrightarrow -1 \leqslant \frac{c}{\sqrt{a^2+b^2}} \leqslant 1\)).
3. On choisit un \(\alpha\) tel que (par exemple) \(\sin(\alpha) = \frac{a}{\sqrt{a^2 + b^2}}\) et \(\cos(\alpha) = \frac{b}{\sqrt{a^2 + b^2}}\).
4. On utilise la formule \[\sin(\alpha)\cos(x) + \cos(\alpha)\sin(x) = \sin(\alpha+x).\]
5. On cherche \(\beta\) tel que (ici on choisit le sinus) \(\sin(\beta) =\frac{c}{\sqrt{a^2+b^2}}\)
6. Finalement on résout \[\sin(\alpha + x) = \sin(\beta).\]

---

Dernière compilation: 2025-06-01 (06:48:34)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)