3.5 Fonctions trigonométriques réciproques

On définit ici les fonctions réciproques des fonctions trigonométriques, on énonce certaines de leurs propriétés, en particulier on calcule leurs dérivées.

Fonction réciproque du sinus

La fonction sinus, vue comme définie sur tout \(\mathbb{R}\), \[\begin{aligned} \sin:\mathbb{R} &\to[-1,1]\\ x&\mapsto \sin(x)\,, \end{aligned}\] est surjective mais pas injective, puisque par exemple des angles supplémentaires ont le même sinus.

On peut par contre la rendre injective en restreignant son domaine.

En effet, si on se restreint à prendre des angles qui sont dans \(IV\cup I\) ou \(II\cup III\) (demi-cercle de gauche ou de droite), c'est à dire dans un intervalle du type \(\left[ \frac{-\pi}{2}+ k\pi, \frac{\pi}{2}+k\pi\right]\) pour un \(k\in\mathbb{Z}\), alors la fonction \[\begin{aligned} \sin:\left[ -\tfrac{\pi}{2} + k\pi, \tfrac{\pi}{2}+k\pi\right] &\to[-1,1]\\ x&\mapsto \sin(x) \end{aligned}\]

est
  1. injective puisque des angles distincts dans son domaine ont des images distinctes,
  2. surjective puisque pour tout \(y\in [-1,1]\) il existe un \(x\in\left[ -\frac{\pi}{2} + k\pi, \frac{\pi}{2}+k\pi\right]\) tel que \(\sin(x)=y\).
  1. Un intervalle du type \(\left[ -\frac{\pi}{2} + k\pi, \frac{\pi}{2}+k\pi\right]\) s'appelle une détermination du sinus. Le sinus y est à la fois injectif et surjectif dans \([-1,1]\), et donc bijectif.
  2. L'intervalle pour \(k=0\), \(\left[ -\frac{\pi}{2} , \frac{\pi}{2}\right]\), s'appelle la détermination principale du sinus.

Une détermination est donc un intervalle sur lequel la fonction \(\sin\) possède une réciproque. La convention est de choisir la détermination principale pour définir une fois pour toute une réciproque:

On définit l'arc sinus comme la réciproque de \[\begin{aligned} \sin:\left[-\tfrac{\pi}{2},\tfrac{\pi}{2}\right] &\to[-1,1]\\ x&\mapsto y=\sin(x)\,. \end{aligned}\] On la note \[\begin{aligned} \arcsin : [-1,1]&\to \left[ \tfrac{-\pi}{2} , \tfrac{\pi}{2}\right] \\ y &\mapsto x = \arcsin(y)\,, \end{aligned}\] où \(x\) est l'unique \(x\in [-\frac{\pi}{2},\frac{\pi}{2}]\) tel que \(\sin(y)=x\).

Comme on sait, le graphe d'une fonction réciproque s'obtient en réfléchissant celui de la fonction à travers la diagonale \(y=x\):

Par définition, \[\begin{aligned} \arcsin(\sin(x))&=x\,\qquad \forall x\in [-\tfrac{\pi}{2},\tfrac{\pi}{2}]\,,\\ \sin(\arcsin(y))&=y\,\qquad \forall y\in [-1,1]\,. \end{aligned}\]

Exemples:

  1. \(\sin(\arcsin(\frac{2}{3}))=\frac23\)
  2. \(\arcsin(\sin(-\frac{\pi}{7}))=-\frac{\pi}{7}\)
  3. \(\arcsin(\sin(\frac{7\pi}{6}))=\)? Puisque \(\frac{7\pi}{6}\notin \left[ \frac{-\pi}{2} , \frac{\pi}{2}\right]\), on doit d'abord trouver l'unique \(x\in[-\frac{\pi}{2},\frac{\pi}{2}]\) tel que \[ \sin\left(\tfrac{7\pi}{6}\right)=\sin(x)\,. \] Cet angle est \(x=-\frac{\pi}{6}\). Donc \[ \arcsin\left(\sin\left(\tfrac{7\pi}{6}\right)\right) = \arcsin\left(\sin\left(-\tfrac{\pi}{6}\right)\right) =-\tfrac{\pi}{6} \]

Avoir une réciproque bien définie pour le sinus permet maintenant de résoudre plus d'équations.

Pour tout \(a\in[-1,1]\), on a \[\sin(x)=a \quad \Leftrightarrow \quad x = \left\{ \begin{array}{l} \arcsin(a) + k2\pi,k \in \mathbb{Z}\,, \\ \text{ou} \\ \pi - \arcsin(a) + k2\pi, k \in \mathbb{Z}\,. \end{array} \right. \]

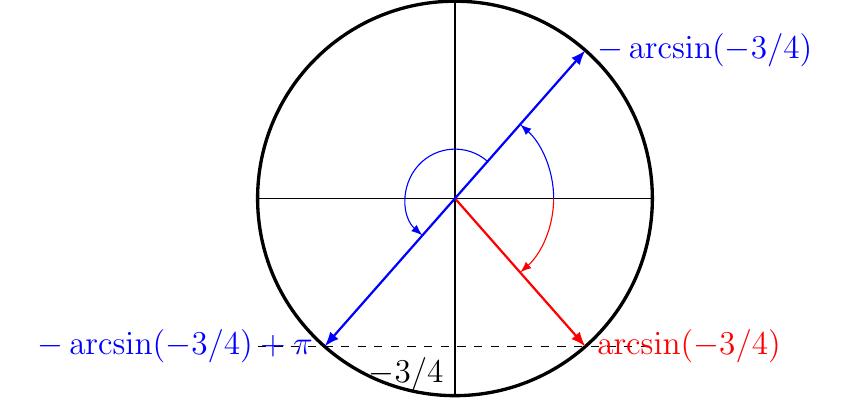
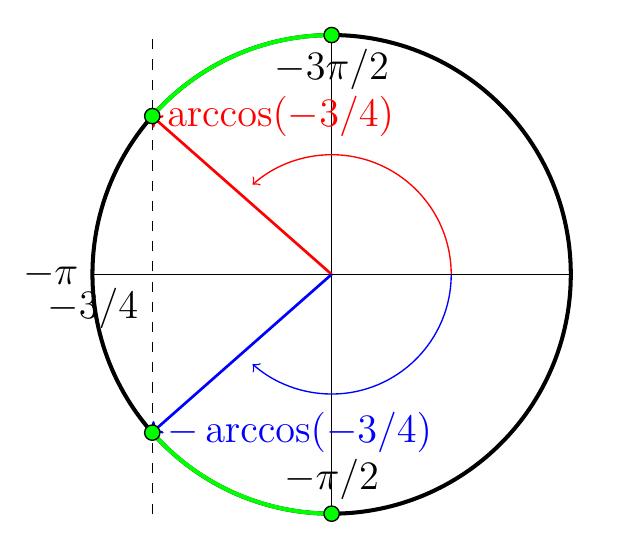
Exemple: Résolvons \[ \sin(x)=-\tfrac{3}{4}\,,\qquad x\in[\pi,2\pi] \]

  1. On résout d'abord sur \(\mathbb{R}\) (sans contrainte). Puisque \(-\frac23\in[-1,1]\), on sait que l'angle \(\alpha=\arcsin(-\frac34)\) permet de récrire l'équation: \[ \sin(x)=\sin(\alpha) \] On a donc comme solutions \[x_1=\arcsin\left(-\tfrac{3}{4}\right) + k2\pi \quad\text{ ou }\quad x_2=\pi-\arcsin\left(-\tfrac{3}{4}\right) + k2\pi\,.\] Plaçons ces solutions sur le cercle trigonométrique.
  2. L'arcsinus d'un nombre négatif est négatif, donc \({\color{red}\arcsin(-\frac34)}\in\left[-\frac{\pi}{2},0\right]\). Pour sélectionner la solution \(x_1\) qui appartient à \([\pi,2\pi]\), on doit donc prendre \(k=1\), à savoir \[ x_1=\arcsin\left(-\tfrac{3}{4}\right) + 2\pi \,. \] Aussi, puisque \(\pi-\arcsin(-\frac34) \in \left[\pi,\frac{3\pi}{2}\right]\subset[\pi,2\pi]\), on peut doit prendre la solution \(x_2\) avec \(k=0\).
En résumé, les solutions de l'équation avec contrainte sont: \[ S= \left\{ \arcsin\left(-\tfrac{3}{4}\right)+2\pi, \pi-\arcsin\left(-\tfrac{3}{4}\right) \right\}\,. \]

Lemme:

  1. Sur \([-1,1]\), \(\arcsin(x)\) est une fonction impaire.
  2. Pour tout \(x\in[-1,1]\), \(\cos(\arcsin(x)) = \sqrt{1-x^2}\)

  1. Si \(x\in[-1,1]\), alors \(-x\in [-1,1]\), et donc \[\sin(\arcsin(-x)) = -x = -\sin(\arcsin(x))=\sin(-\arcsin(x)).\] Dans la dernière égalité on a utilisé le fait que le sinus est impair. Or sur \(\left[ \frac{-\pi}{2} , \frac{\pi}{2}\right]\), \(\sin(x)\) est injective, et donc \[\sin(\arcsin(-x))=\sin(-\arcsin(x)) \quad \Rightarrow \quad \arcsin(-x) = -\arcsin(x)\,. \]
  2. Par la relation \(\sin^2(\alpha)+\cos^2(\alpha)=1\), on a que \[\cos^2(\arcsin(x)) = 1 - \sin^2(\arcsin(x)) = 1-x^2\] Or \(\arcsin(x)\) est un angle dans le quadrant I ou IV, et donc son cosinus est positif, ce qui implique \[ \cos(\arcsin(x)) = +\sqrt{1-x^2}\,. \]

Lemme: L'arc sinus est dérivable sur \(]-1,1[\), et \(\forall x\in ]-1,1[\), \[ \left(\arcsin(x)\right)' = \frac{1}{\sqrt{1-x^2}} \]

On ne montrera pas que \(\arcsin(x)\) est dérivable. Mais pour savoir ce qu'est sa dérivée, on peut partir de \[\sin(\arcsin(x))=x\qquad \forall x\in ]-1,1[\,, \] et dériver des deux côtés de l'équation, et utiliser la règle de dérivation pour une fonction réciproque, \[ \cos(\arcsin(x)) \cdot (\arcsin(x))'=1 \,, \] qui donne \[ (\arcsin(x))'=\frac{1}{\cos(\arcsin(x))}=\frac{1}{\sqrt{1-x^2}} \]

Ce qui vient d'être fait pour le sinus peut être adapté pour les autres fonctions trigonométriques.

Fonction réciproque du cosinus

Vue comme définie sur tout \(\mathbb{R}\), \[\begin{aligned} \cos:\mathbb{R} &\to[-1,1]\\ x&\mapsto \cos(x)\,, \end{aligned}\] est surjective mais pas injective, puisque par exemple des angles opposés ont le même cosinus.

  1. Un intervalle du type \(\left[ k\pi, (k+1)\pi\right]\) pour \(k\in\mathbb{Z}\) s'appelle une détermination du cosinus. Les cosinus y est à la fois injectif et surjectif dans \([-1,1]\), et donc bijectif.
  2. L'intervalle pour \(k=0\), \(\left[ 0, \pi\right]\), s'appelle la détermination principale du cosinus.
On définit l'arc cosinus comme la réciproque de \[\begin{aligned} \cos:[0,\pi] &\to[-1,1]\\ x&\mapsto y=\cos(x)\,. \end{aligned}\] On la note \[\begin{aligned} \arccos : [-1,1]&\to \left[0 , \pi\right] \\ y &\mapsto x = \arccos(y)\,, \end{aligned}\] où \(x\) est l'unique élément de \([0,\pi]\) tel que \(\cos(x)=y\).

Son graphe:

Par définition, \[\begin{aligned} \arccos(\cos(x))&=x\,\qquad \forall x\in [0,\pi]\,,\\ \cos(\arccos(y))&=y\,\qquad \forall y\in [-1,1]\,. \end{aligned}\]

Pour tout \(a\in[-1,1]\), on a \[ \cos(x)=a \quad \Leftrightarrow \quad x=\left\{ \begin{array}{l} \arccos(a) + k2\pi,\quad k \in \mathbb{Z} \\ ou \\ - \arccos(a) + k2\pi,\quad k \in \mathbb{Z}. \end{array} \right. \]

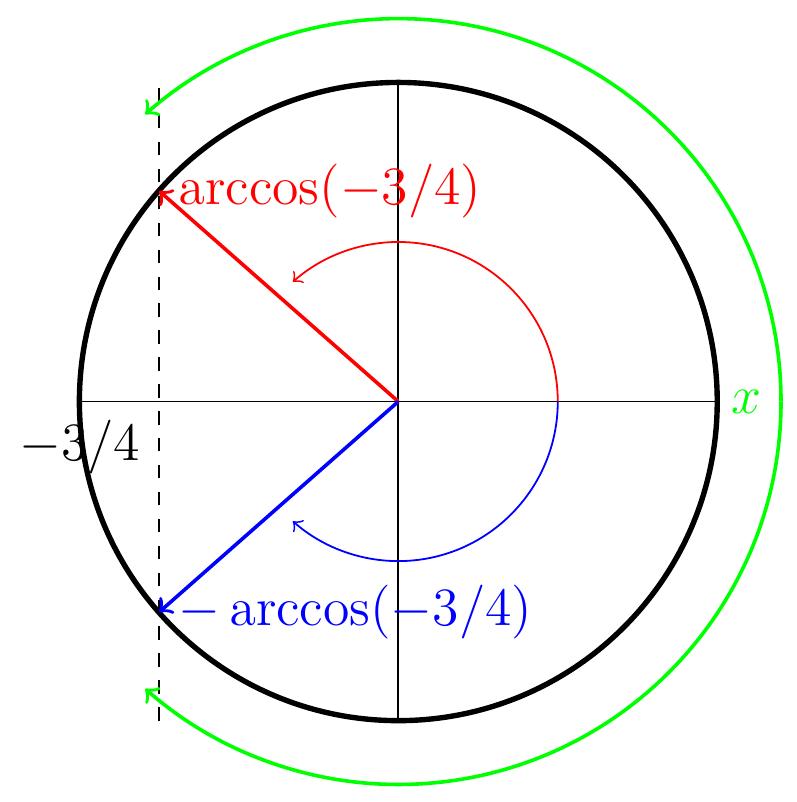
Exemple: Résolvons \[ \cos(x) \geqslant -\tfrac{3}{4}\,,\qquad x\in\left[\tfrac{-3\pi}{2},\tfrac{-\pi}{2}\right] \]

  1. Commençons par étudier le problème sans contrainte, \(x\in \mathbb{R}\). En posant \(\alpha=\arccos(-\frac34)\), l'inéquation devient \[ \cos(x)\geqslant \cos(\alpha)\,, \] donc les solutions sont \[ -\arccos(-\tfrac34) + k2\pi \leqslant x \leqslant \arccos(-\tfrac34)+k2\pi, \qquad k\in \mathbb{Z}.\]
  2. On doit maintenant choisir les solutions dans l'intervalle \(\left[\frac{-3\pi}{2},\frac{-\pi}{2}\right]\). Sur le cercle cela laisse les zones dans les quadrants II et III:
    \(-\arccos(-3/4) \in [-\pi,\frac{-\pi}{2}] \subset \left[\frac{-3\pi}{2},\frac{-\pi}{2}\right]\), donc l'angle est bien placé. \(\arccos(-3/4) \in \left[ \frac{\pi}{2},\pi\right]\), il faut donc faire un tour du cercle dans le sens anti-trigonométrique pour l'amener dans \(\left[-\frac{3\pi}{2},-\pi\right] \subset \left[\frac{-3\pi}{2},\frac{-\pi}{2}\right]\). On garde donc les intervalles \[S = \left[-\tfrac{3\pi}{2},\arccos(-\tfrac34)-2\pi\right] \cup \left[-\arccos(-\tfrac34),-\tfrac{\pi}{2}\right]\,. \]

Lemme:

  1. Pour tout \(x\in[-1,1]\), \(\arccos(-x) =\pi- \arccos(x)\).
  2. Pour tout \(x\in[-1,1]\), \(\sin(\arccos(x)) = \sqrt{1 - x^2}\)

  1. En effet, si \(x\in [-1,1]\), alors \(-x\in [-1,1]\), et donc \[\cos(\arccos(-x)) = -x = -\cos(\arccos(x))=\cos(\pi-\arccos(x)).\] Or sur \(\left[ 0 , \pi\right]\), le cosinus est injectif et donc \[\cos(\arccos(-x))=\cos(\pi-\arccos(x)) \quad\Rightarrow\quad \arccos(-x)=\pi-\arccos(x)\,. \]
  2. Par la relation \(\sin^2(\alpha)+\cos^2(\alpha)=1\), \[\sin^2(\arccos(x)) = 1 - \cos^2(\arccos(x)) = 1-x^2\,.\] Or \(\arccos(x)\) est un angle dans le quadrant I ou II, et donc son sinus est positif, ce qui implique \[\sin(\arccos(x)) = +\sqrt{1-x^2}\,.\]

Lemme: L'arc cosinus est dérivable sur \(]-1,1[\), et \(\forall x\in]-1,1[\), \[ (\arccos(x))' =-\frac{1}{\sqrt{1-x^2}}\,. \]

On ne montrera pas que \(\arccos(x)\) est dérivable. Mais pour savoir ce qu'est sa dérivée, on peut partir de \[\cos(\arccos(x))=x\qquad \forall x\in ]-1,1[\,, \] et dériver des deux côtés de l'équation, et utiliser la règle de dérivation pour une fonction réciproque, \[ -\sin(\arccos(x)) \cdot (\arccos(x))'=1 \,, \] qui donne \[ (\arcsin(x))'=\frac{-1}{\cos(\arcsin(x))}=\frac{-1}{\sqrt{1-x^2}}\,. \]

Exemple: Pour \(x\in[-1,1]\), donner la valeur de \(\alpha=\arcsin(x)+\arccos(x)\).

Pour commencer, on remarque que

Par conséquent, \(\alpha=\arcsin(x)+\arccos(x)\in\left[\frac{-\pi}{2},\frac{3\pi}{2}\right]\).

Calculons \(\sin(\alpha)\). Les formules d'addition donnent \[\begin{aligned} \sin(\arcsin(x)&+\arccos(x))\\ &=\sin(\arcsin(x))\cos(\arccos(x))+\cos(\arcsin(x))\sin(\arccos(x))\\ &= x^2+\sqrt{1-x^2}^2\\ &=1\,. \end{aligned}\] On cherche donc un angle \(\alpha\left[\frac{-\pi}{2},\frac{3\pi}{2}\right]\) tel que \(\sin (\alpha) =1\). Le seul angle avec cette propriété est \(\alpha=\frac{\pi}{2}\). Par conséquent, \[ \arcsin(x)+\arccos(x)=\tfrac{\pi}{2}\qquad \forall x\in [-1,+1]\,. 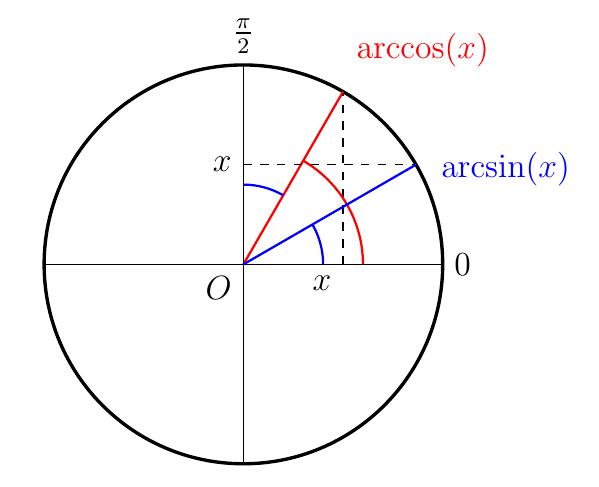\] En d'autres termes: \(\arccos(x)\) et \(\arcsin(x)\) sont donc des angles complémentaires, ce qui est évident d'un point de vue géométrique:

Fonction réciproque de la tangente

La fonction tangente, sur tout son domaine \[\begin{aligned} \tan:\mathbb{R}\setminus\{\tfrac{\pi}{2}+k\pi\,,k\in\mathbb{Z}\} &\to \mathbb{R}\\ x&\mapsto \tan(x)\,, \end{aligned}\] est surjective mais pas injective puisque périodique.

  1. Un intervalle du type \(\left] -\frac{\pi}{2} + k\pi, \frac{\pi}{2}+k\pi\right[\) pour \(k\in\mathbb{Z}\) est une détermination de la tangente. La tangente y est à la fois injective et surjective, et donc bijective.
  2. L'intervalle \(\left] \frac{-\pi}{2} , \frac{\pi}{2}\right[\) s'appelle la détermination principale de la tangente.
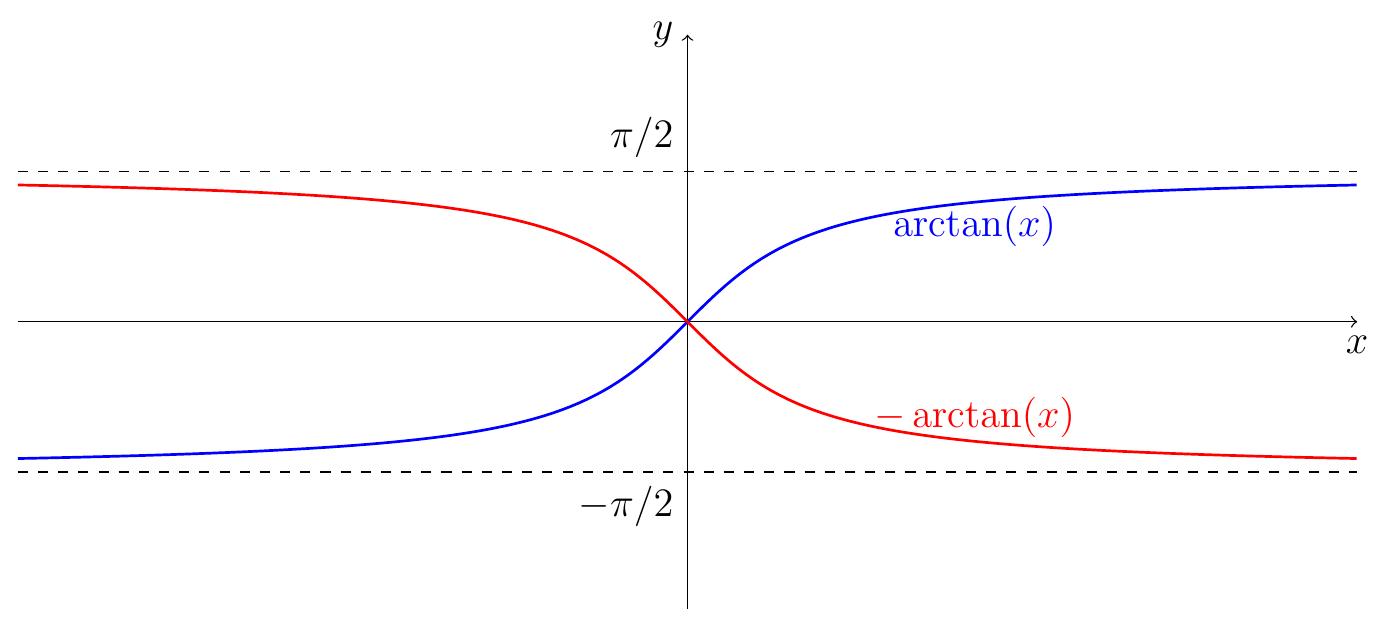
On définit l'arc tangente comme \[\begin{aligned} \arctan: \mathbb{R}&\to ]-\tfrac{\pi}{2},\tfrac{\pi}{2}[\\ y&\mapsto x=\arctan(y)\,, \end{aligned}\] où \(x\) est l'unique angle \(x\in\left]\frac{-\pi}{2},\frac{\pi}{2}\right[\) tel que \(\tan(x)=y\).

Par définition, \[\begin{aligned} \arctan(\tan(x))&=x\,\qquad \forall x\in ]\tfrac{\pi}{2},\tfrac{\pi}{2}[\,,\\ \tan(\arctan(x))&=x\,\qquad \forall x\in \mathbb{R}\,. \end{aligned}\]

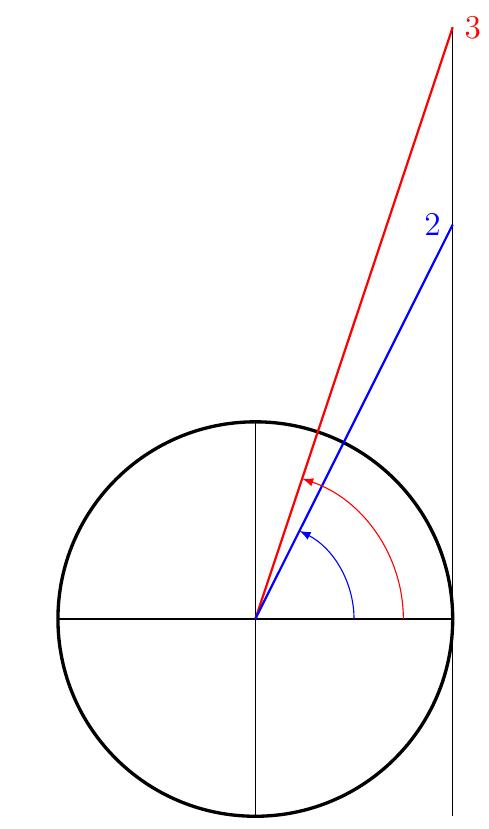
Exemple: Calculer l'angle \(s=\arctan(2) + \arctan(3)\).

  1. On localise \(s\). Comme \(2,3\gt 0\), on a \(\arctan(2),\arctan(3) \in \left]0,\frac{\pi}{2}\right[\). Donc \(s\in]0,\pi[\).
  2. On calcule \(\tan(s)\) à l'aide de la formule d'addition \[\tan(s) = \frac{2+3}{1-2\cdot3} = -1.\] On cherche donc les solutions de l'équation \[\tan(s) = -1\,,\qquad s\in]0,\pi[\] dont l'unique solution est \(\frac{3\pi}{4}.\) On a donc \[ \arctan(2) + \arctan(3) = \frac{3\pi}{4}.\]

Listons encore quelques propriétés.

  1. Pour tout \(a\in\mathbb{R}\), on a \[\tan(x)=a \Leftrightarrow x =\arctan(a) + k\pi,\qquad k \in \mathbb{Z} \]
  2. Pour tout \(x\in\mathbb{R}\), \(\arctan(-x) = -\arctan(x)\).
  3. Pour tout \(x\in\mathbb{R} \), \[ (\arctan(x))'=\frac{1}{1+x^2} \]

    En effet pour tout \(x\in\mathbb{R}\), on a \(\tan(\arctan(x))=x\). En dérivant des deux côtés de l'équation, \[(1+\tan^2(\arctan(x))) \cdot (\arctan(x))'=1 \Leftrightarrow (1+x^2) (\arctan(x))'=1.\]

Fonction réciproque de la cotangente

Pareil pour la cotangente, \[\begin{aligned} \cot:\mathbb{R}\setminus\{k\pi\,,k\in\mathbb{Z}\} &\to \mathbb{R}\\ x&\mapsto \cot(x)\,. \end{aligned}\]

  1. Un intervalle du type \(\left] k\pi, (k+1)\pi\right[\) pour \(k\in\mathbb{Z}\) s'appelle une détermination de la cotangente. La cotangente y est à la fois injective et surjective, donc bijective.
  2. L'intervalle pour \(k=0\), \(\left]0, \pi\right[\), s'appelle la détermination principale de la cotangente.
On définit l'arc cotangente comme \[\begin{aligned} \mathrm{arccot} : \mathbb{R}&\to \left]0 , \pi\right[ \\ y &\mapsto x = \mathrm{arccot}(y)\,, \end{aligned}\] où \(x\) est l'unique \(x\in\left]0, \pi\right[\) tel que \(\cot(x)=y\).

Par définition, \[\begin{aligned} \mathrm{arccot}(\cot(x))&=x\,\qquad \forall x\in ]0,\pi[\,,\\ \cot(\mathrm{arccot}(x))&=x\,\qquad \forall x\in \mathbb{R}\,. \end{aligned}\]

Listons encore quelques propriétés.

  1. Pour tout \(a\in\mathbb{R}\), on a \[\cot(x)=a \Leftrightarrow x =\mathrm{arccot}(a) + k\pi,k \in \mathbb{Z} \]
  2. Pour tout \(x\in\mathbb{R}\), \(\mathrm{arccot}(-x) = \pi-\mathrm{arccot}(x)\).
  3. Pour tout \(x\in\mathbb{R} \), \[(\mathrm{arccot}(x))'=-\frac{1}{1+x^2}\,. \]

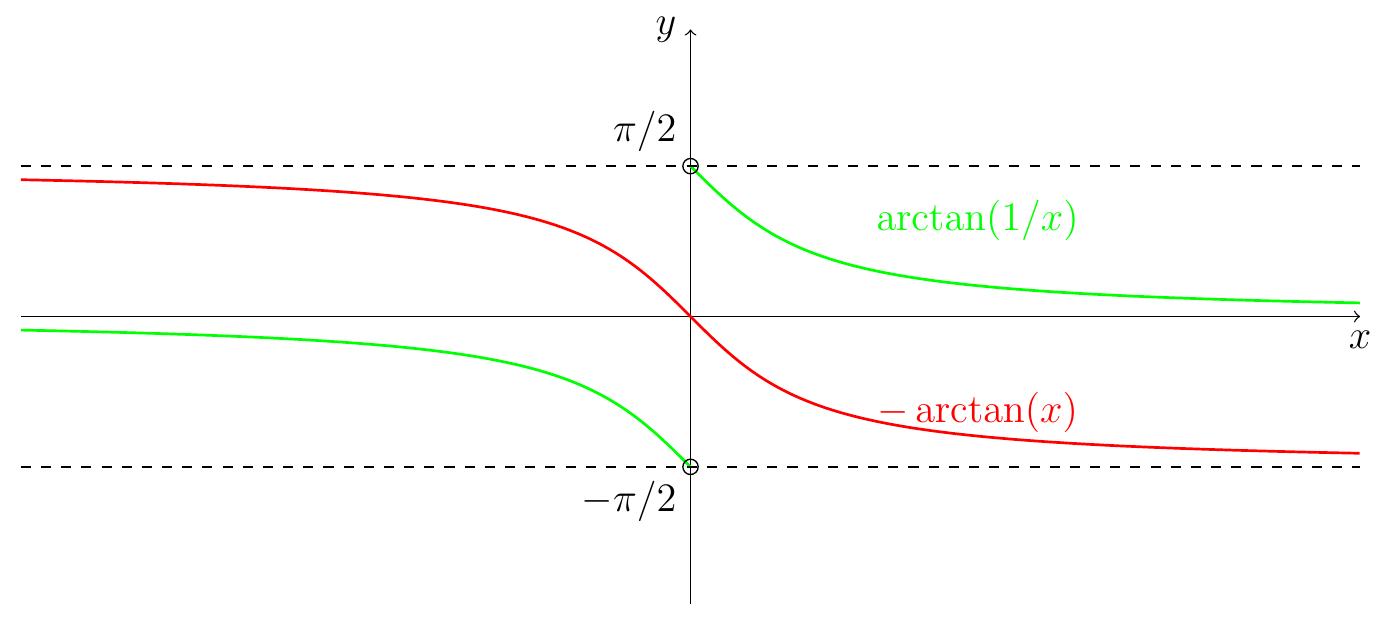
Exemple: A partir du graphe de \(\arctan(x)\), déduire le graphe de \(\displaystyle \arctan\left(\frac{1}{x}\right)\). On pose \[ f(x)=\arctan(x)+\arctan\left(\frac{1}{x}\right)\,. \] Le domaine de définition de \(f\) est \(\mathbb{R}^{*}\). On calcule la dérivée de \(f\): \[f'(x) = \frac{1}{1+x^2} + \frac{1}{1+\frac{1}{x^2}}\frac{-1}{x^2} = \frac{1}{1+x^2} - \frac{1}{1+x^2}=0.\] Par conséquent, \(f\) est une constante sur chaque intervalle continu de son domaine de définition (c'est une conséquence du théorème des accroissements finis). Donc on a \[\arctan(x) + \arctan\left(\frac{1}{x}\right)=\left\{ \begin{array}{l} c_1, x<0 \\ c_2, x>0. \end{array} \right. \] Pour déterminer \(c_1\) et \(c_2\) on évalue la fonction. On a \[\begin{aligned} f(-1)&=\frac{-\pi}{4}+\frac{-\pi}{4}=-\frac{\pi}{2}\,,\\ f(1)&=\frac{\pi}{4}+\frac{\pi}{4}=\frac{\pi}{2}. \end{aligned}\] Par conséquent, on a \(c_1 = -\frac{\pi}{2}\) et \(c_2=\frac{\pi}{2}\) et on conclut que \[\arctan\left(\frac{1}{x}\right) = \mathrm{sgn}(x) \frac{\pi}{2} -\arctan(x).\] Le graphe de \(\arctan\left(\frac{1}{x}\right)\) se construit donc par translation de \(\pm \frac{\pi}{2}\) de celui de \(-\arctan(x)\).

Dernière compilation: 2025-06-01 (06:48:34)

Sauf indication contraire, le contenu de ce document est soumis à une licence Creative Commons internationale, Attribution: Pas d'Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 (CC BY-NC-SA 4.0)