
Exemples:
On considérera les polynômes comme des fonctions complexes,
\(z\mapsto P(z)\).
On notera:
On dit que des polynômes \(P\) et \(Q\) sont égaux, et on note \(P=Q\), lorsque \[ P(z)=Q(z)\qquad \forall z\in\mathbb{C}\,. \]
Théorème: Soient \[\begin{aligned} P(z) &= a_n z^n + a_{n-1} z^{n-1} + ... + a_1 z + a_0, \\ Q(z) &= b_n z^n + b_{n-1} z^{n-1} + ... + b_1z + b_0\,. \end{aligned}\] Alors \(P=Q\) si et seulement \(a_k=b_k\) pour tout \(k=0,1,...,n\).
On somme des polynômes comme on somme des fonctions réelles: si \(P,Q\) sont des polynômes, alors \(P+Q\) est aussi un polynôme, défini par \[ (P+Q)(z)=P(z)+Q(z)\qquad \forall z\in \mathbb{C}\,. \] Concrètement, le coefficient en \(z^k\) de \(P+Q\) s'obtient en additionnant les coefficients de \(P\) et de \(Q\) associés à la puissance \(z^k\).
Exemple: Si \[\begin{aligned} P(z)&=3z^2+5z-6\\ Q(z)&=-z^3-2z^2+3\,, \end{aligned}\] alors \(P+Q\) est \[(P+Q)(z)=P(z)+Q(z)=-z^3+z^2+5z-3\,.\]
En général, \(\deg(P+Q) \leqslant \max\{\deg P,\deg Q\}\).
Exemple: \(P(z)=2z^3+z+1\) est de degré \(3\), \(Q(z)=-2z^3+3z^2-5\) est de degré \(3\), mais \((P+Q)(z)=3z^2+z-4\) est de degré \(2\).
Soient \(P\) est un polynôme et \(\lambda\in\mathbb{C}\) est un scalaire (nombre fixé), le produit de \(P\) par \(\lambda\) , noté \(\lambda P\) , est le polynôme \(\lambda P\in\mathbb{C}[z]\) défini en multipliant chaque coefficient de \(P\) par \(\lambda\) .
Exemple: Si \(P(z)=3z^2+5z-6\) et \(\lambda=-\frac{2}{3}\), alors \[(\lambda P)(z)=\lambda P(z)={}-2z^2-\frac{10}{3}z+4\,.\]
Remarquons que \[ \deg(\lambda P)= \begin{cases} 0&\text{ si }\lambda=0\,,\\ \deg(P)&\text{ si }\lambda\neq 0\,. \end{cases} \] Avec les deux opérations définies ci-dessus (addition de polynômes et multiplication d'un polynôme par un scalaire) \(\mathbb{C}[z]\), \(\mathbb{R}[z]\) et \(P_n[z]\) sont des exemples d'espaces vectoriels.
On multiplie des polynômes comme on multiplie des fonctions réelles: si \(P,Q\) sont des polynômes, alors \(PQ\) est aussi un polynôme, défini par \[ (PQ)(z)=P(z)Q(z)\qquad \forall z\in \mathbb{C}\,. \]
Exemple: Soient \(P(z)=3z^2+5z-6\) et \(Q(z)={}-z^3-2z^2+3\). \[\begin{aligned} (PQ)(z)&=P(z)Q(z)\\ &=(3z^2+5z-6)({}-z^3-2z^2+3) \\ &=-3z^5-6z^4+9z^2 -5z^4-10z^3+15z +6z^3+12z^2-18\\ &=-3z^5 -11z^4 -4z^3 +21z^2+15z-18 . \end{aligned}\]
Remarquons que \[ \deg(PQ)=\deg P+\deg Q \]
Exemple:
Il est important de noter que la réductibilité d'un polynôme dépend du
type de polynômes que l'on souhaite voir apparaître dans la factorisation.
En effet, la possibilité d'une factorisation \(P=P_1P_2\) dépend de ce qui est
exigé sur \(P_1\) et \(P_2\): si on exige que \(P_1,P_2\in\mathbb{R}[z]\), la
factorisation n'est pas toujours possible.
Donc un polynôme peut être irréductible dans \(\mathbb{R}[z]\) mais pas dans \(\mathbb{C}[z]\)!
Exemple: Soit \(P(z)=z^2+1\), qui est à coefficients réels.
Nous verrons plus bas que si \(z_0\) est une racine de \(P\), alors \(P\) peut s'écrire comme \(P(z) = (z-z_0) Q(z)\) où \(Q\) est un polynôme de degré plus petit. Les seuls polynômes irréductibles dans \(\mathbb{C}[z]\) sont donc les polynômes de degré 1. Dans \(\mathbb{R}[z]\), les seuls autres polynômes irréductibles sont les polynômes de degré 2 à discriminants négatifs.
Une question naturelle, si on se donne un polynôme \(P\), est de trouver les racines de \(P\), à savoir les \(z\) tels que \[ P(z)=0\,. \]
Rechercher les racines de \(P\) (dans \(\mathbb{C}\) ou \(\mathbb{R}\)) et factoriser
\(P\) (en un produit de facteurs irréductibles dans ces mêmes ensembles)
sont des problèmes équivalentes. Nous l'avions déjà constaté dans le cas
particulier de l'étude des trinômes du second degré.
Donnons quelques exemples de factorisations.
Exemple: Trouver les décompositions en facteurs irréductibles de \(P(z)=z^4-z^2-2z-1\). Par les identités remarquables (voir fin de section), on a \[\begin{aligned} P(z) &=z^4-(z^2+2z+1) \\ &= (z^2)^2 - (z+1)^2 \\ &= (z^2-(z+1))(z^2+z+1) \\ &=(z^2-z-1)(z^2+z+1) \\ &= (z-z_1)(z-z_2)(z^2+z+1)\,, \end{aligned}\] où \(z_1=\frac{1-\sqrt{5}}{2}\), \(z_2=\frac{1+\sqrt{5}}{2}\). Comme le discriminant de \(z^2+z+1\) est strictement négatif, il ne peut pas être factorisé comme produit de polynômes à coefficients réels et donc la décomposition dans \(\mathbb{R}[z]\) de \(P\) est \[P(z)=(z-z_1)(z-z_2)(z^2+z+1).\] Si on travaille à présent dans \(\mathbb{C}[z]\), on peut autoriser des polynômes à coefficients complexes dans la décomposition, et en reprenant l'expression du dessus, nous pouvons écrire \[\begin{aligned} z^2+z+1=(z-w_1)(z-w_2)\,, \end{aligned}\] où \(w_1=\frac{-1-\sqrt{3}i}{2}\), \(w_2=\frac{-1+\sqrt{3}i}{2}\). La décomposition en facteurs irréductibles de \(P\) dans \(\mathbb{C}[z]\) est donc \[P(z)=(z-z_1)(z-z_2)(z-w_1)(z-w_2).\]
Dans l'exemple précédent, nous avons pu factoriser le polynôme en utilisant les identités remarquables et le discriminant. Dans le cas où la factorisation n'est pas évidente, on recherche une racine particulière \(z_0\) et on divise \(P(z)\) par le binôme \((z-z_0)\).
Théorème: Soient \(P\) un polynôme, \(\deg P \geqslant 1\), et \(z_0\in\mathbb{C}\). Il existe alors un unique polynôme \(F\) tel que \[P(z)=(z-z_0)F(z)+P(z_0)\,.\] De plus, on a \(\deg F = \deg P -1\)
On prouve ce théorème par une vérification directe.
Supposons que \(P\) est de degré \(n\), de la forme suivante:
\[
P(z)=a_n z^n+a_{n-1} z^{n-1} + \cdots + a_1 z + a_0\,.
\]
Fixons un \(z_0\in\mathbb{C}\) quelconque, et cherchons un polynôme \(F\) de degré
\(n-1\) tel que
\[
P(z)=(z-z_0)F(z)+P(z_0)\qquad \forall z\in\mathbb{C}\,.
\]
Nommons \(b_k\) les coefficients du polynôme recherché:
\[
F(z)=b_{n-1} z^{n-1} + b_{n-2} z^{n-2} + \cdots + b_1 z + b_0\,.
\]
Commençons par développer:
\[\begin{aligned}
(z-z_0)F(z)&= (b_{n-1} z^{n-1} + b_{n-2} z^{n-2} + \cdots
+ b_1 z + b_0)(z-z_0)\\
&= b_{n-1} z^n + (b_{n-2} - b_{n-1}z_0) z^{n-1} + \cdots
+ (b_0-b_1z_0)z- b_0z_0
\end{aligned}\]
En posant
\[\begin{array}{rcl}
b_{n-1} &=& a_n \\
b_{n-2} &=& a_{n-1} + b_{n-1}z_0 \\
&\vdots& \\
b_{1} &=& a_{2} + b_{2}z_0 \\
b_0 &=& a_1 + b_1z_0\,,
\end{array}\]
on peut récrire cette dernière comme suit
\[
(z-z_0)F(z)=-z_0b_0+P(z)-a_0\,.
\]
Puisque cette dernière est vraie en particulier pour \(z=z_0\), on en tire la
relation
\(P(z_0) = a_0 + b_0z_0\), qui permet donc d'écrire
\[
(z-z_0)F(z)=P(z)-P(z_0)\,,
\]
ce qui conclut la preuve.
La façon dont les coefficients \(b_k\) sont définis récursivement ci-dessus, à
savoir \(b_j=a_{j+1}+z_0b_{j+1}\), peut se résumer dans un shéma appelé
shéma de Hörner:

Dans la première colonne, on descend le coefficient \(a_n\) pour obtenir \(b_{n-1}\), puis on effectue le produit croisé avec \(z_0\). Par la suite, on somme les résultats de chaque colonne pour obtenir le nouveau coefficient \(b_k\) et on reproduit la procédure jusqu'à arriver au bout du tableau.
Quelques remarques concernant la relation obtenue dans le théorème ci-dessus: \[ P(z)=(z-z_0)F(z)+P(z_0). \]
Remarque: S'il existe \(n\in\mathbb{N}^{*}\) et un polynôme \(F(z)\) tel que \(F(z_0)\neq 0\) et \[P(z) = (z-z_0)^n F(z)\,, \] on dit que \(z_0\) est une racine d'ordre (ou de multiplicité) \(n\). Cas particuliers : si \(n=1\), on parle de racine simple, si \(n=2\) on parle de racine double.
Exemple: Effectuer la division de \(P(x) = x^3 + 7x^2 + 4x -12\) par \(x-1\).
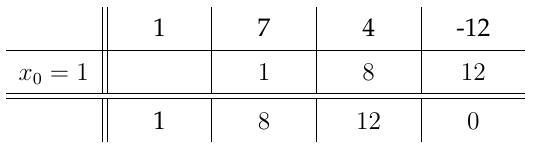
Exemple: Effectuer la division de \(P(x)=x^3 + 8x^2 + 17x + 10\) par \(x+1\). Ici il faut voir que \(x_0=-1\) et par conséquent on effectue la division de \(P(x)\) par \(x-(-1)\). On a par Hörner
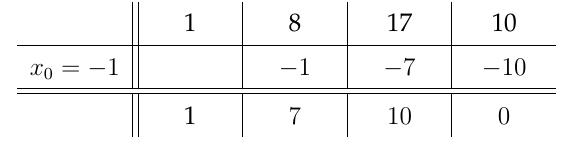
Exemple: Résoudre l'équation \(3x^3-2x^2+4x+9=0\). On observe que \(x_0=-1\) est
racine évidente de \(P(x)=3x^3-2x^2+4x+9\). \(P(x)\) est donc divisible par
\(x+1\). Par Hörner, on obtient
\[P(x)=(x+1)(3x^2-5x+9)\,.\]
Ici la décomposition dans \(\mathbb{R}\) s'arrête car \(3x^2-5x+9\) n'a aucune racine
réelle (\(\Delta \lt 0\)). L'équation \(P(x)=0\) pour \(x\in\mathbb{R}\) admet donc comme
ensemble solution \(S=\{1\}.\)
Si on résout à présent \(P(x)=0\) pour \(x\in\mathbb{C}\), on peut factoriser \(P\)
comme
\[
P(x) = (x+1)(3x^2-5x+9)=3(x+1)(x-x_+)(x-x_-)\,,
\]
avec \(x_\pm = \frac{5 \pm \sqrt{83}i}{6}\),
et donc l'ensemble solution est \(S=\{-1,x_-,x_+\}\).
Exemple: Effectuer la division de \(P(x)=4x^3+2\) par \(x+2\).
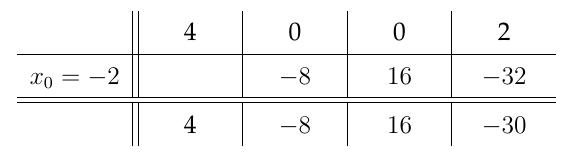
Théorème: Tout polynôme \(P\in\mathbb{C}[z]\) possède au moins une racine complexe.
Exemple: \(z_0=1+i\) est solution de l'équation \(z^{17}+122i z^3-12-12i=0\).
Par le Théorème Fondamental, les seuls polynômes irréductibles de \(\mathbb{C}[z]\) sont du premier degré.
Théorème: Soit \(P \in\mathbb{R}[z]\) un polynôme à coefficients réels. Alors, si \(z\) est une racine de \(P\), son complexe conjugué \(\bar{z}\) est aussi racine de \(P\).
En effet, soit \(P(z)=a_n z^n+a_{n-1} z^{n-1} + \cdots + a_1 z + a_0\) avec \(a_k\in\mathbb{R},\: k=0,\ldots,n\). Alors \[\begin{aligned} 0= P(z) \quad\Leftrightarrow\quad 0 &= \overline{P(z)} \\ &= \overline{ a_n z^n+a_{n-1} z^{n-1} + \cdots + a_1 z + a_0} \\ &= a_n \bar{z}^n+a_{n-1} \bar{z}^{n-1} + \cdots + a_1 \bar{z} + a_0 \\ &= P(\bar{z}). \end{aligned}\]
Théorème: Tout polynôme \(P\in\mathbb{R}[x]\) peut être décomposé en facteurs irréductibles de \(\mathbb{R}[x]\): \[P(x)=a(x-x_1)^{n_1}\cdots(x-x_p)^{n_p}(x^2+\beta_1x+\gamma_1)^{m_1}\cdots(x^2+\beta_qx+\gamma_q)^{m_q}\] avec
Preuve : En effet supposons que \(P\) est un polynôme réel de degré strictment plus grand que 2 ou de degré 2 mais avec un discriminant non négatif. \(P\), à titre de cas particulier d'un polynôme à coefficients complexes, possède au moins une racine \(z_0\in\mathbb{C}\).
Exemple: Décomposer \(P(x)=x^4+1\) en facteurs irréductibles dans \(\mathbb{R}[x]\).
Les coefficients \(\binom{n}{k}\), dans la formule du binôme, sont appelés coefficients binomiaux et peuvent se calculer à l'aide du triangle de Pascal: $$\begin{array}{c|llllll|ccccc} n=0 & (x+a)^0= & 1 &&&&& 1 \\ n=1 & (x+a)^1= & x &+a&&&& 1 & 1 \\ n=2 & (x+a)^2= & x^2 &+2ax& + a^2 &&& 1 & 2 & 1 \\ n=3 & (x+a)^3= & x^3 &+3ax^2&+3a^2x&+x^3&& 1 & \textcolor{red}{3} & \textcolor{red}{3} & 1 \\ n=4 & (x+a)^4= & x^4 & + 4ax^3& +6a^2 x^2 & + 4a^3x &+a^4 & 1 & 4 & \textcolor{red}{6} & 4 & 1 \\ \hline k &&&&&&& 0 & 1 & 2 & 3 & 4 \end{array} $$ On construit le triangle de Pascal avec les deux règles suivantes :